
- •1.Системы координат
- •2. Векторы и операци над веторами
- •5. Скалярное произведение. Свойства высчисления
- •Скалярное произведение в координатах.
- •Свойства скалярного произведения.
- •Вычисление скалярного произведения, примеры и решения.
- •6.Вексторное произведение. Свойства вычисления.
- •Свойства векторного произведения
- •7.Смешанное произведение.Свойста вычисления. Свойства смешанного произведения
- •8.Линейные образы на плоскости.
- •9. Кривые 2 порядка
- •10.Линейные образы в пространстве.
- •11. Поверхности второго порядка.
- •12.Матрицы, правило крамера.
- •Разложение по строке или столбцу
- •Правило Саррюса
- •Свойства определителей
- •Решение систем уравнений
- •Нахождение обратной матрицы
- •13. Теорема Крамера Капелли, метод гаусса
- •Решение систем линейных уравнений методом Крамера.
- •14.Фундаментальный набор решений однородной системы уравнений.
- •15.Функции. Последовательность как функция дискретного аргумента.
- •16. Бескоечно большие, бесконечно малые и ограниченные велечины и их свойства.
- •Предел функции
- •4.4. Правила предельного перехода
- •4.5. Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •17.Арифметическое свойство придела.
- •18. Первый замечательный предел.
- •19.Второй замечательный предел.
- •20. Сравнение бесконечно малых величин. Бесконечно малые функции. Сравнение бесконечно малых
- •Сравнение бесконечно малых функций
- •21.Неперывность ффункции, классификация точекк разрыва.
- •22.Производная и ее свойства.
- •Правила дифференцирования
- •Основные формулы дифференцирования.
- •23. Производная сложной и обратной функции.
- •24.Геометрический смысл производной.
- •25. Дефференциал.
- •Геометрический смысл дифференциала
- •26. Теорема лагранжа о конечном приращении.
- •27. Теорема ролля Теорема Ролля
- •28. Теорема ферма Теорема Ферма
- •29.Теорема коши
- •30. Монотонность и экстремумы функции. Применение производной. Монотонность функции, основные понятия и определения
- •Связь монотонности функции с ее производной
- •31. Асимптоты. Точки перегиба. Построение графиков функций
- •32. Логарифмическое дифференцирование.
- •Случай независимой переменной
- •Случай зависимой переменной
- •34. Формула тейлора
- •Формула Тейлора
- •35. Функции нескольких переменных. Непрерывность. Дифференцируемость.
- •36. Повторное дифференцирование.
- •37. Геометрический смысл частных производных.
- •38. Дифференциал функции нескольких переменных.
- •39. Производная по направлению. Градиент.
- •40. Дифференцирование сложной функции нескольких переменных.
- •41. Экстремумы функции нескольких переменных.
- •42. Условные экстремумы. Метод множителей Лагранжа
22.Производная и ее свойства.
Определение: Пусть
функция ![]() определена
в точке
определена
в точке![]() и
в некоторой ее окрестности. Дадим
аргументу
и
в некоторой ее окрестности. Дадим
аргументу![]() приращение
приращение![]() ,
такое, чтобы не выйти из указанной
окрестности. Найдем соответствующее
приращение функции
,
такое, чтобы не выйти из указанной
окрестности. Найдем соответствующее
приращение функции![]() и
составим отношение. Если существует
предел этого отношения при
и
составим отношение. Если существует
предел этого отношения при![]() стремящемся
к нулю, то указанный предел называют
производной функции
стремящемся
к нулю, то указанный предел называют
производной функции![]() в
точке
в
точке![]() и
обозначают
и
обозначают![]() .
Иначе говоря:
.
Иначе говоря:
![]() (
(![]() —
приращение функции,
—
приращение функции,![]() —
приращение аргумента).
—
приращение аргумента).
Если
в каждой точке ![]() из
множества
из
множества![]() у
функции
у
функции![]() существует
производная, то такая функция называется
дифференцируемой на множестве
существует
производная, то такая функция называется
дифференцируемой на множестве![]() .
.
Геометрический
смысл производной: ![]() —
угловой коэффициент касательной к
графику функции
—
угловой коэффициент касательной к
графику функции![]() в
точке
в
точке![]() уравнение
касательной в
этой точке
уравнение
касательной в
этой точке ![]() .
.
Правила дифференцирования
Пусть
функции ![]() и
и![]() определены
и дифференцируемы на некотором
множестве
определены
и дифференцируемы на некотором
множестве![]() ,
,![]() и
и![]() —
любые действительные числа. Тогда на
множестве
—
любые действительные числа. Тогда на
множестве![]() справедливы
соотношения:
справедливы
соотношения:
 ,
, ,
, ,
,  ,
,
Основные формулы дифференцирования.
23. Производная сложной и обратной функции.
Пусть у = f(и) и u = φ(х)- тогда у = f(φ{x)) — сложная функция с промежуточным аргументом и н независимым аргументом х.
 По
условию
По
условию ![]() Отсюда,
по теореме о связи функции, ее предела
и бесконечно малой функции, имеем
Отсюда,
по теореме о связи функции, ее предела
и бесконечно малой функции, имеем
![]() или
или![]() где
где![]() .
Функцияu
= φ(х) имеет
производную в точке х:
.
Функцияu
= φ(х) имеет
производную в точке х: ![]() ,
поэтому
,
поэтому![]() Подставив
значение Δи в
равенство (20.6), получим
Подставив
значение Δи в
равенство (20.6), получим
![]() т.е.
т.е.![]() Разделив
полученное равенство на Δх и
перейдя к пределу при Δх→0,
получим
Разделив
полученное равенство на Δх и
перейдя к пределу при Δх→0,
получим ![]() Итак,
для нахождения производной сложной
функции надопроизводную
данной функции по промежуточному
аргументу умножить на производную
промежуточного аргумента по независимому
аргументу.
Это
правило остается в силе, если промежуточных
аргументов несколько. Так, если у
= f(u), u = φ(v), v
= g{х),
то
Итак,
для нахождения производной сложной
функции надопроизводную
данной функции по промежуточному
аргументу умножить на производную
промежуточного аргумента по независимому
аргументу.
Это
правило остается в силе, если промежуточных
аргументов несколько. Так, если у
= f(u), u = φ(v), v
= g{х),
то ![]() Пустьу
= f(x) и х
= φ(y)—
взаимно обратные функции.
Пустьу
= f(x) и х
= φ(y)—
взаимно обратные функции.
 Рассмотрим
обратную функциюх
= φ(y).
Дадим аргументу у приращение
Δу ≠
0. Ему соответствует приращение Δх обратной
функции, причем Δх
≠ 0
в силу строгой монотонности функции у
= f(x).
Поэтому можно записать
Рассмотрим
обратную функциюх
= φ(y).
Дадим аргументу у приращение
Δу ≠
0. Ему соответствует приращение Δх обратной
функции, причем Δх
≠ 0
в силу строгой монотонности функции у
= f(x).
Поэтому можно записать  Если
Δy→0,
то в силу непрерывности обратной функции
приращение Δх→0.
И так как
Если
Δy→0,
то в силу непрерывности обратной функции
приращение Δх→0.
И так как ![]() ,
то из (20.7) следуют равенства
,
то из (20.7) следуют равенства
Таким
образом, производная
обратной функции равна обратной величине
производной данной функции.
Правило
дифференцирования обратной функции
записывают так:
 Пример
1.
Найти производную функции
Пример
1.
Найти производную функции ![]() Решение:
Данная функция является сложной. Ее
можно представить в виде цепочки
«простых» функций:
Решение:
Данная функция является сложной. Ее
можно представить в виде цепочки
«простых» функций: ![]() ,
где
,
где![]() ,
гдеz
= tg q, где
q =.
,
гдеz
= tg q, где
q =.![]() .
По правилу дифференцирования сложной
функции (
.
По правилу дифференцирования сложной
функции (![]()
![]() )получаем:
)получаем: Пример
2.
Пользуясь правилом дифференцирования
обратной функции, найти производную
Пример
2.
Пользуясь правилом дифференцирования
обратной функции, найти производную ![]() для
функции
для
функции![]() Решение:
Обратная функция
Решение:
Обратная функция ![]() имеет
производную
имеет
производную![]() .
Следовательно,
.
Следовательно,
24.Геометрический смысл производной.
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y= f(x) в этой точке.

Рассмотрим график функции y = f ( x ):
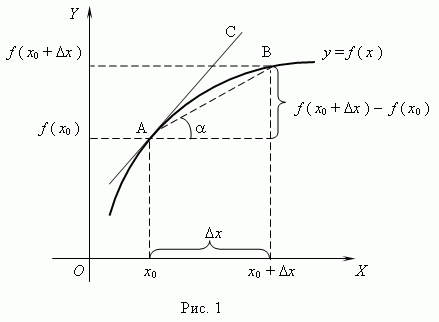
Из
рис.1 видно, что для любых двух
точек A и B графика
функции: ![]() xf(x0+
xf(x0+![]() x)−f(x0)=tg
x)−f(x0)=tg![]() ,
где
,
где ![]() -
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то
-
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то ![]() x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:
x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
