
- •1.Системы координат
- •2. Векторы и операци над веторами
- •5. Скалярное произведение. Свойства высчисления
- •Скалярное произведение в координатах.
- •Свойства скалярного произведения.
- •Вычисление скалярного произведения, примеры и решения.
- •6.Вексторное произведение. Свойства вычисления.
- •Свойства векторного произведения
- •7.Смешанное произведение.Свойста вычисления. Свойства смешанного произведения
- •8.Линейные образы на плоскости.
- •9. Кривые 2 порядка
- •10.Линейные образы в пространстве.
- •11. Поверхности второго порядка.
- •12.Матрицы, правило крамера.
- •Разложение по строке или столбцу
- •Правило Саррюса
- •Свойства определителей
- •Решение систем уравнений
- •Нахождение обратной матрицы
- •13. Теорема Крамера Капелли, метод гаусса
- •Решение систем линейных уравнений методом Крамера.
- •14.Фундаментальный набор решений однородной системы уравнений.
- •15.Функции. Последовательность как функция дискретного аргумента.
- •16. Бескоечно большие, бесконечно малые и ограниченные велечины и их свойства.
- •Предел функции
- •4.4. Правила предельного перехода
- •4.5. Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •17.Арифметическое свойство придела.
- •18. Первый замечательный предел.
- •19.Второй замечательный предел.
- •20. Сравнение бесконечно малых величин. Бесконечно малые функции. Сравнение бесконечно малых
- •Сравнение бесконечно малых функций
- •21.Неперывность ффункции, классификация точекк разрыва.
- •22.Производная и ее свойства.
- •Правила дифференцирования
- •Основные формулы дифференцирования.
- •23. Производная сложной и обратной функции.
- •24.Геометрический смысл производной.
- •25. Дефференциал.
- •Геометрический смысл дифференциала
- •26. Теорема лагранжа о конечном приращении.
- •27. Теорема ролля Теорема Ролля
- •28. Теорема ферма Теорема Ферма
- •29.Теорема коши
- •30. Монотонность и экстремумы функции. Применение производной. Монотонность функции, основные понятия и определения
- •Связь монотонности функции с ее производной
- •31. Асимптоты. Точки перегиба. Построение графиков функций
- •32. Логарифмическое дифференцирование.
- •Случай независимой переменной
- •Случай зависимой переменной
- •34. Формула тейлора
- •Формула Тейлора
- •35. Функции нескольких переменных. Непрерывность. Дифференцируемость.
- •36. Повторное дифференцирование.
- •37. Геометрический смысл частных производных.
- •38. Дифференциал функции нескольких переменных.
- •39. Производная по направлению. Градиент.
- •40. Дифференцирование сложной функции нескольких переменных.
- •41. Экстремумы функции нескольких переменных.
- •42. Условные экстремумы. Метод множителей Лагранжа
19.Второй замечательный предел.
Число e (число
Эйлера) является
иррациональным и приблизительно равно ![]() .
Это число принято за основание логарифмов,
которые называют натуральными логарифмами
и обозначают lnx (lnx=logex)
.
Это число принято за основание логарифмов,
которые называют натуральными логарифмами
и обозначают lnx (lnx=logex)
Второй замечательный
или
в другой записи

В
случае второго замечательного предела
имеем дело с неопределенностью вида
единица в степени бесконечность ![]() .
.
Разберем несколько примеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.
Пример.
Вычислить
предел 
Решение.
Подставляем
бесконечность:

Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.
Сделаем
замену переменных. Пусть
![]()
Если ![]() ,
то
,
то ![]()
Исходный
предел после замены примет вид:

Ответ:

Пример.
Вычислить
предел 
Решение.
Подставляем
бесконечность:

Пришли
к неопределенности единица в степени
бесконечность, которая указывает на
применение второго замечательного
предела. Выделим целую часть в основании
показательно степенной функции:
![]()
Тогда
предел запишется в виде:

Сделаем
замену переменных. Пусть
![]()
Если ![]() ,
то
,
то ![]()
Исходный
предел после замены примет вид:
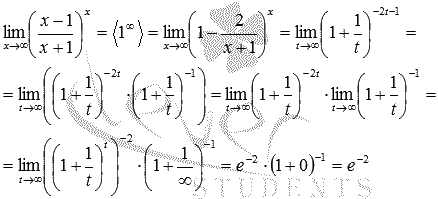
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:

Пример.
Вычислить
предел 
Решение.

Преобразуем
функцию, чтобы применить второй
замечательный предел:
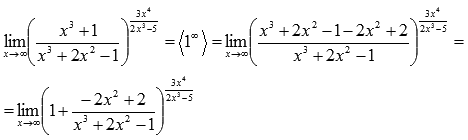
Сейчас
домножим показатель на ![]() и
разделим на это же выражение, затем
используем свойства степени:
и
разделим на это же выражение, затем
используем свойства степени:

Так
как показатели степени числителя и
знаменателя дроби  одинаковые
(они равны 6),
то предел этой дроби на бесконечности
равен отношению коэффициентов при
старших степенях (см.
непосредственное вычисление пределов):
одинаковые
(они равны 6),
то предел этой дроби на бесконечности
равен отношению коэффициентов при
старших степенях (см.
непосредственное вычисление пределов):

Если
произвести замену ![]() ,
то получим второй замечательный предел
в чистом виде, следовательно,
,
то получим второй замечательный предел
в чистом виде, следовательно,

Ответ:

20. Сравнение бесконечно малых величин. Бесконечно малые функции. Сравнение бесконечно малых
Что
тут сказать… Если существует предел ![]() ,
то функция
,
то функция ![]() называетсябесконечно
малой в точке
называетсябесконечно
малой в точке ![]() .
.
Существенным моментом утверждения является тот факт, что функция может быть бесконечно малой лишь в конкретной точке.
Начертим
знакомую линию ![]() :
:
 Данная
функция бесконечно
малА в
единственной точке:
Данная
функция бесконечно
малА в
единственной точке: ![]() Следует
отметить что, в точках «плюс бесконечность»
и «минус бесконечность» эта же функция
будет уже бесконечно
большой:
Следует
отметить что, в точках «плюс бесконечность»
и «минус бесконечность» эта же функция
будет уже бесконечно
большой: ![]() .
Или в более компактной записи:
.
Или в более компактной записи: ![]()
Во всех других точках, предел функции будет равен конечному числу, отличному от нуля.
Таким образом, не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке.
! Примечание: для краткости я часто буду говорить «бесконечно малая функция», подразумевая, что она бесконечно малА в рассматриваемой точке.
Таких
точек может быть несколько и даже
бесконечно много. Изобразим какую-нибудь
непуганую параболу:
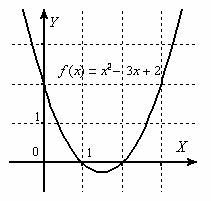 Представленная
квадратичная функция является бесконечно
малой в двух точках – в «единице» и в
«двойке»:
Представленная
квадратичная функция является бесконечно
малой в двух точках – в «единице» и в
«двойке»: ![]()
Как
и в предыдущем примере, на бесконечности
данная функция является бесконечно
большой: ![]()
Смысл
двойных знаков:
Запись ![]() обозначает,
что при
обозначает,
что при ![]() ,
а при
,
а при ![]() .
Запись
.
Запись ![]() обозначает,
что при
обозначает,
что при ![]() ,
а при
,
а при ![]() .
Запись
.
Запись ![]() обозначает,
что и при
обозначает,
что и при ![]() ,
и при
,
и при ![]() .
Запись
.
Запись ![]() обозначает,
что и при
обозначает,
что и при ![]() ,
и при
,
и при ![]() .
Прокомментированный
принцип «расшифровки» двойных знаков
справедлив не только для бесконечностей,
но и для любых конечных точек, функций
и ряда других математических объектов.
.
Прокомментированный
принцип «расшифровки» двойных знаков
справедлив не только для бесконечностей,
но и для любых конечных точек, функций
и ряда других математических объектов.
А
теперь синус ![]() .
Это пример, когда функция бесконечно
малА в
бесконечном количестве точек:
.
Это пример, когда функция бесконечно
малА в
бесконечном количестве точек:
![]() Действительно,
синусоида «прошивает» ось абсцисс через
каждое «пи»:
Действительно,
синусоида «прошивает» ось абсцисс через
каждое «пи»: Заметьте,
что сверху/снизу функция ограничена, и
не существует такой точки, в которой бы
она была бесконечно
большой,
синусу остаётся разве что облизываться
на бесконечность.
Заметьте,
что сверху/снизу функция ограничена, и
не существует такой точки, в которой бы
она была бесконечно
большой,
синусу остаётся разве что облизываться
на бесконечность.
Отвечу ещё на пару простых вопросов:
Может ли функция быть бесконечно малой на бесконечности?
Конечно.
Таких экземпляров воз и маленькая
тележка.
Элементарный
пример: ![]() .
Геометрический смысл данного предела,
к слову, проиллюстрирован в статье Графики
и свойства функций.
.
Геометрический смысл данного предела,
к слову, проиллюстрирован в статье Графики
и свойства функций.
Может ли функция НЕ БЫТЬ бесконечно малой? (в любой точке области определения)
Да.
Очевидный пример – квадратичная функция,
график которой (парабола) не пересекает
ось ![]() .
Обратное утверждение, кстати, в общем
случае неверно – гипербола из предыдущего
вопроса, хоть и не пересекает ось абсцисс,
но бесконечно
малА на
бесконечности.
.
Обратное утверждение, кстати, в общем
случае неверно – гипербола из предыдущего
вопроса, хоть и не пересекает ось абсцисс,
но бесконечно
малА на
бесконечности.
