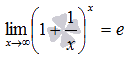4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
Пусть f1 (x)
и
f 2 (x)
бесконечно малые величины при 
,
т.е.
и
.
1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
.
(4.17)
2. Произведение бесконечно малых величин есть величина бесконечно малая:
.
(4.18)
3.
Произведение бесконечно малой величины
на константу С или
на функцию, имеющую конечный предел 
,
есть величина бесконечно малая:
.
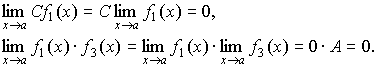(4.19)
Пусть 
и
бесконечно
большие величины при
,
т.е.
и
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
.
(4.20)
2. Произведение бесконечно больших величин есть величина бесконечно большая:
.
(4.21)
3.
Произведение бесконечно большой величины
на константу С,
или на функцию, имеющую конечный предел 
,
есть величина бесконечно большая:
(4.22)
Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть 
и
,
тогда
и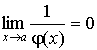
.
Символически можно записать:
и
Примеры:
1) 
;
2) 
;
3) 
.
П р и м е ч а н и е. При вычислении пределов возможны следующие комбинации бесконечно малых и бесконечно больших величин, которые называются неопределенностями:
.
17.Арифметическое свойство придела.
Арифметические свойства предела функции. Пусть функции f и g определены на интервале ( a, b ), кроме быть может точки x0. Если существует пределы
и 
,
то существуют пределы в левых частях равенств и имеют место эти равенства :
a. 
б. 
Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей. 2. Если
,
то
существует проколатая окрестность 
точки
,
где функцияf ( x ) ограничена.
Действительно,
если взять 
=
1 
0,
то из существования конечного предела
следует, что существует 
0,
что для всех x :
0 
|x - x0 | 
,
выполняется | f ( x )
- A | 
1,
отсюда, | f ( x )
| - | A | 
|f ( x )
- A | 
1,
т.е.
3. Если
,
то
существует проколотая окрестность 
точки
,
что для всехx 
:
Действительно,
возьмем 
0,
тогда из существования конечного
предела, следует, что существует
окрестность 
,
что для всехx 
:
4. Свойства, связанные с неравенствами. Если
, 
и
для всех x 
:f ( x ) 
g ( x )
, то A 
B
Если
= 
=A
и
для всех x 
:
,то
существует
Доказательства этих свойств следуют из следующих свойств для сходящихся последовательностей и определения предела функции по Гейне.
18. Первый замечательный предел.
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Первый
замечательный предел имеет
вид: 
На
практике чаще встречаются модификации
первого замечательного предела в
виде
где, k – коэффициент.
Пояснение:
Следствия первого замечательного предела:
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.
Разберем несколько примеров нахождения предела по первому замечательному пределу сподробным оприсанием решения.
Пример.
Найти
предел не пользуясь правилом Лопиталя 
Решение.
Подставляем
значение:
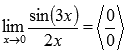
Пришли
к неопределенности ноль делить на ноль.
Смотрим в таблицу
неопределенностей для
определения метода решения. Комбинация
синуса и его аргумента подсказывает
нам о применении первого замечательного
предела, но для этого сначала нужно
немного преобразовать выражение.
Домножим на 3х и
числитель и знаменатель дроби.
В
силу следствия из первого замечательного
предела 
,
поэтому приходим к результату:
Ответ:
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:
Пришли
к неопределенности ноль делить на ноль.
Преобразуем числитель, используя формулы
тригонометрии.
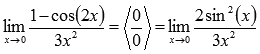
Стало
видно, что здесь можно применить первый
замечательный предел:
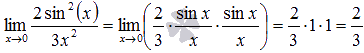
Ответ:
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:
Пришли к неопределенности ноль делить на ноль. Сделаем замену.
Пусть
,
следовательно, 
при 
.
Тогда
предел после замены переменной примет
вид:
Ответ:
предел имеет
вид:
