
- •1.Системы координат
- •2. Векторы и операци над веторами
- •5. Скалярное произведение. Свойства высчисления
- •Скалярное произведение в координатах.
- •Свойства скалярного произведения.
- •Вычисление скалярного произведения, примеры и решения.
- •6.Вексторное произведение. Свойства вычисления.
- •Свойства векторного произведения
- •7.Смешанное произведение.Свойста вычисления. Свойства смешанного произведения
- •8.Линейные образы на плоскости.
- •9. Кривые 2 порядка
- •10.Линейные образы в пространстве.
- •11. Поверхности второго порядка.
- •12.Матрицы, правило крамера.
- •Разложение по строке или столбцу
- •Правило Саррюса
- •Свойства определителей
- •Решение систем уравнений
- •Нахождение обратной матрицы
- •13. Теорема Крамера Капелли, метод гаусса
- •Решение систем линейных уравнений методом Крамера.
- •14.Фундаментальный набор решений однородной системы уравнений.
- •15.Функции. Последовательность как функция дискретного аргумента.
- •16. Бескоечно большие, бесконечно малые и ограниченные велечины и их свойства.
- •Предел функции
- •4.4. Правила предельного перехода
- •4.5. Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •17.Арифметическое свойство придела.
- •18. Первый замечательный предел.
- •19.Второй замечательный предел.
- •20. Сравнение бесконечно малых величин. Бесконечно малые функции. Сравнение бесконечно малых
- •Сравнение бесконечно малых функций
- •21.Неперывность ффункции, классификация точекк разрыва.
- •22.Производная и ее свойства.
- •Правила дифференцирования
- •Основные формулы дифференцирования.
- •23. Производная сложной и обратной функции.
- •24.Геометрический смысл производной.
- •25. Дефференциал.
- •Геометрический смысл дифференциала
- •26. Теорема лагранжа о конечном приращении.
- •27. Теорема ролля Теорема Ролля
- •28. Теорема ферма Теорема Ферма
- •29.Теорема коши
- •30. Монотонность и экстремумы функции. Применение производной. Монотонность функции, основные понятия и определения
- •Связь монотонности функции с ее производной
- •31. Асимптоты. Точки перегиба. Построение графиков функций
- •32. Логарифмическое дифференцирование.
- •Случай независимой переменной
- •Случай зависимой переменной
- •34. Формула тейлора
- •Формула Тейлора
- •35. Функции нескольких переменных. Непрерывность. Дифференцируемость.
- •36. Повторное дифференцирование.
- •37. Геометрический смысл частных производных.
- •38. Дифференциал функции нескольких переменных.
- •39. Производная по направлению. Градиент.
- •40. Дифференцирование сложной функции нескольких переменных.
- •41. Экстремумы функции нескольких переменных.
- •42. Условные экстремумы. Метод множителей Лагранжа
1.Системы координат
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декартаположение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.
Прямоугольная
система координат на плоскости образуется
двумя взаимно перпендикулярными осями
координат ![]() и
и ![]() (крестом).
Оси координат пересекаются в точке
(крестом).
Оси координат пересекаются в точке ![]() ,
которая называется началом
координат,
на каждой оси выбрано положительное
направление.
,
которая называется началом
координат,
на каждой оси выбрано положительное
направление.
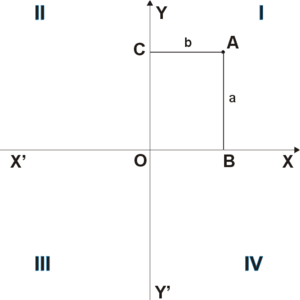
![]()
Рис. 1
Положение
точки ![]() на
плоскости определяется двумя
координатами
на
плоскости определяется двумя
координатами ![]() и
и ![]() .
Координата
.
Координата ![]() равна
длине отрезка
равна
длине отрезка ![]() ,
координата
,
координата ![]() —
длине отрезка
—
длине отрезка ![]() в
выбранных единицах измерения.
Отрезки
в
выбранных единицах измерения.
Отрезки ![]() и
и ![]() определяются
линиями, проведёнными из точки
определяются
линиями, проведёнными из точки ![]() параллельно
осям
параллельно
осям ![]() и
и ![]() соответственно.
соответственно.
При
этом координате ![]() приписывается
знак минус, если точка
приписывается
знак минус, если точка ![]() лежит
на луче
лежит
на луче ![]() (а
не на луче
(а
не на луче ![]() ,
как на рисунке). Координате
,
как на рисунке). Координате ![]() приписывается
знак минус, если точка
приписывается
знак минус, если точка ![]() лежит
на луче
лежит
на луче ![]() .
Таким образом,
.
Таким образом,![]() и
и ![]() являются
отрицательными направлениями осей
координат (каждая ось координат
рассматривается как числовая
ось).
являются
отрицательными направлениями осей
координат (каждая ось координат
рассматривается как числовая
ось).
Координата ![]() называется абсциссой точки
называется абсциссой точки ![]() ,
координата
,
координата ![]() — ординатой точки
— ординатой точки ![]() .
.
Символически это записывают так:
![]()
или
![]()
или указывают принадлежность координат конкретной точке с помощью индекса:
![]()
и т. д.
В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси
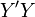 вверх,
ось
вверх,
ось 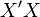 смотрела
направо. Обычно принято пользоваться
правосторонними системами координат
(если обратное не оговорено или не
очевидно — например, из чертежа;
иногда по каким-то соображениям бывает
удобнее всё же пользоваться левосторонней системой
координат).
смотрела
направо. Обычно принято пользоваться
правосторонними системами координат
(если обратное не оговорено или не
очевидно — например, из чертежа;
иногда по каким-то соображениям бывает
удобнее всё же пользоваться левосторонней системой
координат).Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат
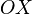 ,
, 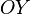 и
и 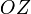 .
Оси координат пересекаются в точке
.
Оси координат пересекаются в точке 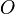 ,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно (не обязательно[2])
одинаковы для всех осей.
,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно (не обязательно[2])
одинаковы для всех осей. 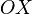 — ось
абсцисс,
— ось
абсцисс, 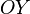 — ось
ординат,
— ось
ординат, 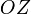 — ось
аппликат.
— ось
аппликат.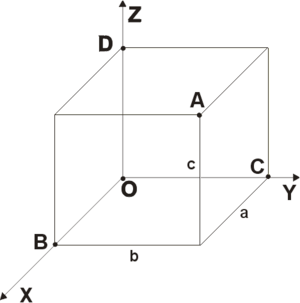

Рис. 2
Положение точки
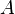 в
пространстве определяется тремя
координатами
в
пространстве определяется тремя
координатами 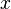 ,
, 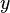 и
и 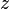 .
Координата
.
Координата 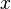 равна
длине отрезка
равна
длине отрезка 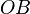 ,
координата
,
координата 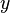 —
длине отрезка
—
длине отрезка 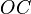 ,
координата
,
координата 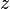 —
длине отрезка
—
длине отрезка 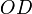 в
выбранных единицах измерения.
Отрезки
в
выбранных единицах измерения.
Отрезки 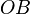 ,
, 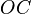 и
и 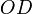 определяются
плоскостями, проведёнными из
точки
определяются
плоскостями, проведёнными из
точки 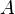 параллельно
плоскостям
параллельно
плоскостям 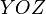 ,
, 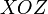 и
и 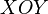 соответственно.
соответственно.Координата
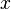 называется
абсциссой точки
называется
абсциссой точки 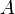 ,
,координата
 —
ординатой точки
—
ординатой точки 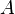 ,
,координата
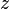 — аппликатой точки
— аппликатой точки 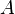 .
.Символически это записывают так:
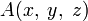
или
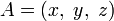
или привязывают запись координат к конкретной точке с помощью индекса:
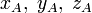
и т. п.
Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка
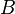 лежала
не как на рисунке — на луче
лежала
не как на рисунке — на луче 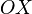 ,
а на его продолжении в обратную сторону
от точки
,
а на его продолжении в обратную сторону
от точки 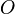 (на
отрицательной части оси
(на
отрицательной части оси 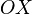 ),
то абсцисса
),
то абсцисса 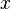 точки
точки 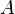 была
бы отрицательной (минус расстоянию
была
бы отрицательной (минус расстоянию 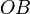 ).
Аналогично и для двух других осей.
).
Аналогично и для двух других осей.Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются терминыположительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси
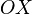 против
часовой стрелки на 90° её положительное
направление совпало с положительным
направлением оси
против
часовой стрелки на 90° её положительное
направление совпало с положительным
направлением оси 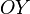 ,
если этот поворот наблюдать со стороны
положительного направления оси
,
если этот поворот наблюдать со стороны
положительного направления оси 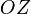 ).
).
