
- •Глава 1. Векторная алгебра
- •§1. Основные понятия векторной алгебры
- •§2. Проекция вектора на ось.
- •§3. Координаты вектора
- •§4. Скалярное произведение векторов
- •§5. Векторное произведение векторов
- •§5. Смешанное произведение векторов
- •Глава 2. Прямая на плоскости
- •§1. Уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярной заданному вектору
- •§2. Параметрические и канонические уравнения прямой на плоскости
- •§3. Взаимное расположение прямых на плоскости
- •§4. Расстояние от точки до прямой
- •§5. Уравнение прямой с угловым коэффициентом
- •Глава 3. Плоскость в пространстве.
- •§1. Уравнение плоскости в пространстве
- •§ 2. Взаимное расположение плоскостей в пространстве
- •Глава 4. Прямая в пространстве
- •§1. Общие уравнения прямой в пространстве
- •§2. Параметрические и канонические уравнения прямой в пространстве
- •§ 3. Переход от одного вида уравнения прямой к другому виду
- •§4. Взаимное расположение прямых в пространстве. Угол между прямыми.
- •Глава 5. Взаимное расположение прямой и плоскости
§3. Координаты вектора
До сих пор считалось, что векторы
рассматриваются в пространстве. Начиная
с этого момента будим считать, что все
векторы рассматриваются на плоскости.
Будем также полагать, что на плоскости
задана Декартова система координат
(даже если об этом не говорится),
представляющая две взаимно перпендикулярные
числовые оси – горизонтальная ось
![]() и
вертикальная ось
и
вертикальная ось![]() .
Тогда каждой точке
.
Тогда каждой точке![]() на
плоскости ставится в соответствие пара
чисел
на
плоскости ставится в соответствие пара
чисел![]() ,
которые являются ее координатами.
Обратно, каждой паре чисел
,
которые являются ее координатами.
Обратно, каждой паре чисел![]() соответствует точка плоскости такая,
что пара чисел
соответствует точка плоскости такая,
что пара чисел![]() являются ее координатами.
являются ее координатами.

Рис. 19.
Из элементарной геометрии известно,
что если на плоскости имеются две точки
![]() и
и![]() ,
то расстояние
,
то расстояние![]() между
этими точками выражается через их
координаты по формуле
между
этими точками выражается через их
координаты по формуле
![]() .
.
Пусть на плоскости задана Декартова
система координат. Орт оси
![]() будем обозначать символом
будем обозначать символом![]() ,
а орт оси
,
а орт оси![]() символом
символом![]() .
Проекцию произвольного
.
Проекцию произвольного![]() вектора
вектора![]() на ось
на ось![]() будем обозначать символом
будем обозначать символом![]() ,
а проекцию на ось
,
а проекцию на ось![]() символом
символом![]() .
.

Рис. 20.
Пусть
![]() - произвольный вектор на плоскости.
Имеет место следующая теорема.
- произвольный вектор на плоскости.
Имеет место следующая теорема.
Теорема 22.
Для любого вектора
![]() на плоскости существует пара чисел
на плоскости существует пара чисел![]() таких, что справедливо равенство
таких, что справедливо равенство
![]() .
.
При этом
![]() ,
,![]() .
.
Доказательство.

Рис. 21.
Пусть дан вектор![]() .
Отложим вектор
.
Отложим вектор![]() от начала координат. Обозначим через
от начала координат. Обозначим через![]() вектор-проекцию вектора
вектор-проекцию вектора![]() на ось
на ось![]() ,
а через
,
а через![]() вектор-проекцию вектора
вектор-проекцию вектора![]() на ось
на ось![]() .
Тогда, как видно из рисунка 21, имеет
место равенство
.
Тогда, как видно из рисунка 21, имеет
место равенство
![]() .
.
![]() Согласно
теореме 9,
Согласно
теореме 9,
![]() ,
,
![]() .
.
Обозначим
![]() ,
,![]() .
Тогда получаем
.
Тогда получаем
![]() .
.
Итак, доказано, что для любого вектора
![]() существует пара чисел
существует пара чисел![]() таких, что справедливо равенство
таких, что справедливо равенство
![]() ,
,
Причем,
![]() ,
,
![]() .
.
При другом расположении вектора
![]() относительно осей доказательство
аналогично.
относительно осей доказательство
аналогично.
Определение.
Пара чисел
![]() и
и![]() таких, что
таких, что![]() ,
называются координатами вектора
,
называются координатами вектора![]() .
Число
.
Число![]() называется иксовой координатой, а число
называется иксовой координатой, а число![]() игрековой координатой.
игрековой координатой.
Определение.
Пара ортов осей координат
![]() называется ортонормированным базисом
на плоскости. Представление любого
вектора
называется ортонормированным базисом
на плоскости. Представление любого
вектора![]() в виде
в виде![]() называется разложением вектора
называется разложением вектора![]() по базису
по базису![]() .
.
Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.
Теорема.
Равные векторы имеют равные координаты.
Доказательство.
Пусть
![]() ,
,
![]()
и
![]() .
Докажем, что
.
Докажем, что![]() ,
,![]() .
.
Из равенства векторов следует, что
![]() .
.
Отсюда
![]() .
.
Допустим, что
![]() ,
а
,
а![]() .
.
Тогда
![]() и значит
и значит![]() ,
что не верно. Аналогично, если
,
что не верно. Аналогично, если![]() ,
но
,
но![]() ,
то
,
то![]() .
Отсюда
.
Отсюда![]() ,
что не верно. Наконец, если допустить,
что
,
что не верно. Наконец, если допустить,
что![]() и
и![]() ,
то получаем, что
,
то получаем, что
![]() .
.
Это означает, что векторы
![]() и
и![]() коллинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что
коллинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что![]() ,
,![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Таким образом, координаты вектора
полностью определяют сам вектор. Зная
координаты
![]() и
и![]() вектора
вектора![]() можно построить сам вектор
можно построить сам вектор![]() , построив векторы
, построив векторы![]() и
и![]() и сложив их. Поэтому часто сам вектор
и сложив их. Поэтому часто сам вектор![]() обозначают в виде пары его координат и
пишут
обозначают в виде пары его координат и
пишут![]() .
Такая запись означает, что
.
Такая запись означает, что![]() .
.
Непосредственно из определения координат вектора следует следующая теорема.
Теорема.
При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде
![]() ,
,
![]() .
.
Доказательство.
![]() ,
,
![]() .
.
Далее установим как связаны координаты вектора с координатами его концов.
Теорема.
Пусть
![]() ,
причем начало вектора точка
,
причем начало вектора точка![]() имеет координаты
имеет координаты![]() ,
а конец вектора есть точка
,
а конец вектора есть точка![]() .
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
.
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
![]() ,
,
![]() .
.
Доказательство.
Пусть
![]() и пусть вектор-проекция вектора
и пусть вектор-проекция вектора![]() на ось
на ось![]()
![]() сонаправлен с осью
сонаправлен с осью![]() (см. рис. 22). Тогда
(см. рис. 22). Тогда
![]() ,
,
т ак
как длина отрезка на числовой оси
ак
как длина отрезка на числовой оси![]() равна координате правого конца минус
координата левого конца. Если вектор
равна координате правого конца минус
координата левого конца. Если вектор![]()
![]()
Рис. 22.
![]() противонаправлен оси
противонаправлен оси![]() (как
на Рис. 23), то
(как
на Рис. 23), то
![]() .
.
 Рис. 23.
Рис. 23.
Если
![]() ,
то в этом случае
,
то в этом случае![]() и тогда получаем
и тогда получаем
![]() .
.
Таким образом, при любом расположении
вектора
![]() относительно
осей координат его координата
относительно
осей координат его координата![]() равна
равна
![]() .
.
Аналогично доказывается, что
![]() .
.
Пример.
Даны координаты концов вектора
![]() :
:![]() .
Найти координаты вектора
.
Найти координаты вектора![]() .
.
Решение.
![]() .
.
В следующей теореме приводится выражение длины вектора через его координаты.
Теорема 15.
Пусть
![]() .Тогда
.Тогда
![]() .
.
Доказательство.
Пусть
![]() и
и![]() - вектор-проекции вектора
- вектор-проекции вектора![]() на оси
на оси![]() и
и![]() ,
соответственно. Тогда, как показано при
доказательстве теоремы 9, имеет место
равенство
,
соответственно. Тогда, как показано при
доказательстве теоремы 9, имеет место
равенство
![]() .
.
При этом, векторы
![]() и
и![]() взаимно перпендикулярны. При сложении
этих векторов по правилу треугольника
получаем прямоугольный треугольник
(см. Рис. 24).
взаимно перпендикулярны. При сложении
этих векторов по правилу треугольника
получаем прямоугольный треугольник
(см. Рис. 24).

Рис. 24.
По теореме Пифагора имеем
![]() .
.
Но
![]() ,
,
![]() .
.
Следовательно
![]() ,
,
![]() .
.
Отсюда
![]() .
.
Или
![]() .
.
Пример.
![]() .Найти
.Найти![]() .
.
Решение.
![]() .
.
Введем понятие направляющих косинусов вектора .
Определение.
Пусть вектор
![]() составляет с осью
составляет с осью![]() угол
угол![]() ,
а с осью
,
а с осью![]() угол
угол![]() (см. Рис. 25).
(см. Рис. 25).

Рис. 25.
Тогда
![]() ,
,
![]() .
.
Следовательно,
![]()
Так как для любого вектора
![]() имеет место равенство
имеет место равенство
![]() ,
,
Где
![]() - орт вектора
- орт вектора![]() ,
то есть вектор единичной длины,
сонаправленный с вектором
,
то есть вектор единичной длины,
сонаправленный с вектором![]() ,
то
,
то
![]() .
.
Вектор
![]() определяет направление вектора
определяет направление вектора![]() .
Его координаты
.
Его координаты![]() и
и![]() называются направляющими косинусами
вектора
называются направляющими косинусами
вектора![]() .
Направляющие косинусы вектора можно
выразить через его координаты по формулам
.
Направляющие косинусы вектора можно
выразить через его координаты по формулам
![]() ,
,
![]() .
.
Имеет место соотношение
![]()
![]() .
.
До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.
Будем считать, что в пространстве
задана Декартова система координат с
осями
![]() ,
,![]() и
и![]() .
.
Орты осей
![]() ,
,![]() и
и![]() будем обозначать символами
будем обозначать символами![]() ,
,![]() и
и![]() ,
соответственно (Рис. 26).
,
соответственно (Рис. 26).
Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для
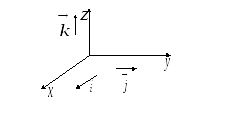 Рис. 26.
Рис. 26.
векторов в пространстве. Тройка векторов
![]() называется ортонормированным базисом
в пространстве.
называется ортонормированным базисом
в пространстве.
Пусть
![]() ,
,![]() и
и![]() - вектор-проекции вектора
- вектор-проекции вектора![]() на
оси
на
оси![]() ,
,![]() и
и![]() ,
соответственно. Тогда
,
соответственно. Тогда
![]() .
.
В свою очередь
![]() ,
,
![]() ,
,
![]() .
.
Если обозначить
![]() ,
,
![]() ,
,
![]() ,
,
То получаем равенство
![]() .
.
Коэффициенты перед базисными векторами
![]() ,
,![]() и
и![]() называются координатами вектора
называются координатами вектора![]() .
Таким образом, для любого вектора
.
Таким образом, для любого вектора![]() в пространстве существует тройка чисел
в пространстве существует тройка чисел![]() ,
,![]() ,
,![]() ,
называемых координатами вектора
,
называемых координатами вектора![]() таких,
что для этого вектора справедливо
представление
таких,
что для этого вектора справедливо
представление
![]() .
.
Вектор
![]() в этом случае также обозначают в виде
в этом случае также обозначают в виде![]() .
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
.
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() -
угол между вектором
-
угол между вектором![]() и осью
и осью![]() ,
,![]() -
угол между вектором
-
угол между вектором![]() и осью
и осью![]() ,
,![]() - угол между вектором
- угол между вектором![]() и осью
и осью![]() .
.
Длина вектора
![]() выражается через его координаты по
формуле
выражается через его координаты по
формуле
![]() .
.
Справедливы утверждения о том, что
равные векторы имеют равные координаты,
при сложении векторов их координаты
складываются, а при умножении вектора
на число его координаты умножаются на
это число.
![]() ,
,![]() и
и![]() называются
направляющими косинусами вектора
называются
направляющими косинусами вектора![]() .
Они связаны с координатами вектора
формулами
.
Они связаны с координатами вектора
формулами
![]() ,
,![]() ,
,![]() .
.
Отсюда следует соотношение
![]() .
.
Если концы вектора
![]() имеют
координаты
имеют
координаты![]() ,
,![]() ,
то координаты вектора
,
то координаты вектора![]() связаны с координатами концов вектора
соотношениями
связаны с координатами концов вектора
соотношениями
![]() ,
,
![]() ,
,
![]() .
.
Пример.
Даны точки
![]() и
и![]() .
Найти координаты вектора
.
Найти координаты вектора![]() .
.
Решение.
![]() .
.
