§ 3. Переход от одного вида уравнения прямой к другому виду

Как показано выше, уравнения одой и той же прямой можно записать по крайней мере в трех видах: общие уравнения прямой, параметрические уравнения прямой и канонические уравнения прямой. Рассмотрим вопрос о переходе от уравнений прямой одного вида к уравнениям прямой в другом виде.

Во-первых заметим, что если заданы уравнения прямой в параметрической форме, то тем самым заданы точка, через которую проходит прямая и направляющий вектор прямой. Поэтому не составляет труда записать уравнения прямой в канонической форме.

Пример.

Даны уравнения прямой в параметрической форме

.

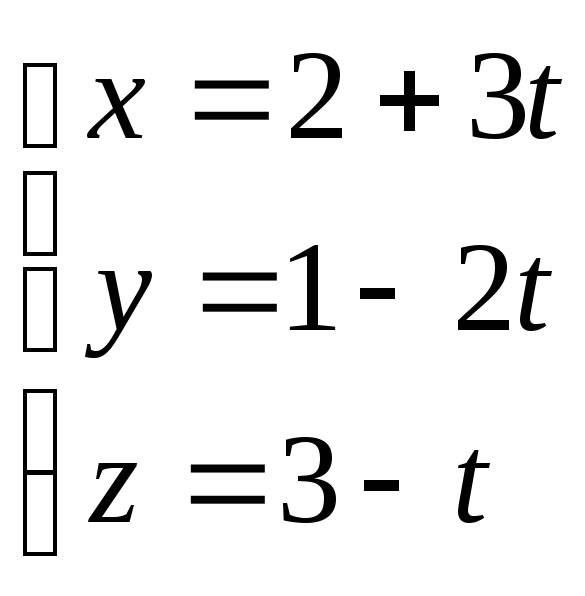Записать канонические уравнения прямой.

Решение.

Прямая проходит через точку и имеет направляющий вектор. Следовательно, канонические уравнения прямой имеют вид

.

Аналогично решается задача о переходе от канонических уравнений прямой к параметрическим уравнениям прямой.

Переход от канонических уравнений прямой к общим уравнениям прямой рассматривается ниже на примере.

Пример.

Даны канонические уравнения прямой

.

Записать общие уравнения прямой.

Решение.

Запишем канонические уравнения прямой в виде системы двух уравнений

.

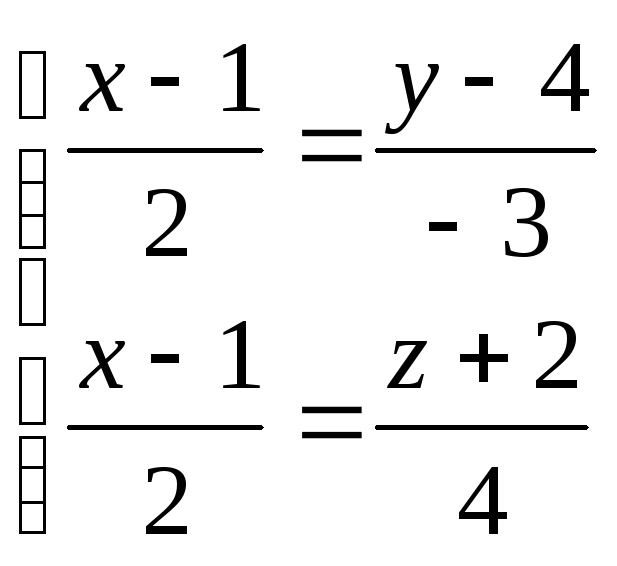Избавляясь от знаменателей путем умножения обеих частей первого уравнения на 6, а второго уравнения на 4, получим систему

.

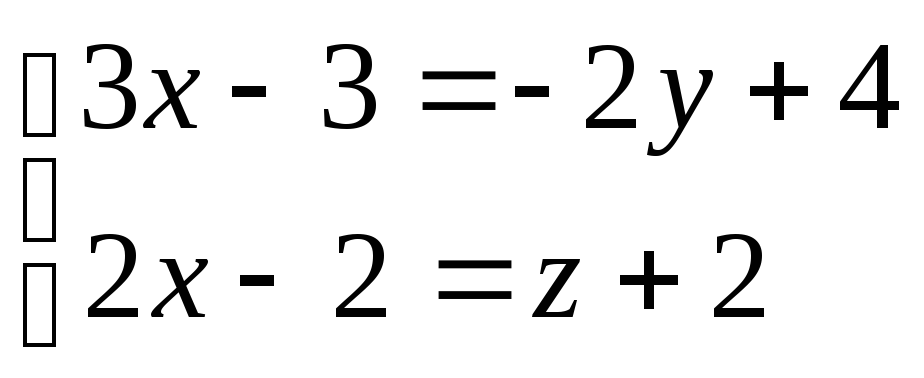Или

.

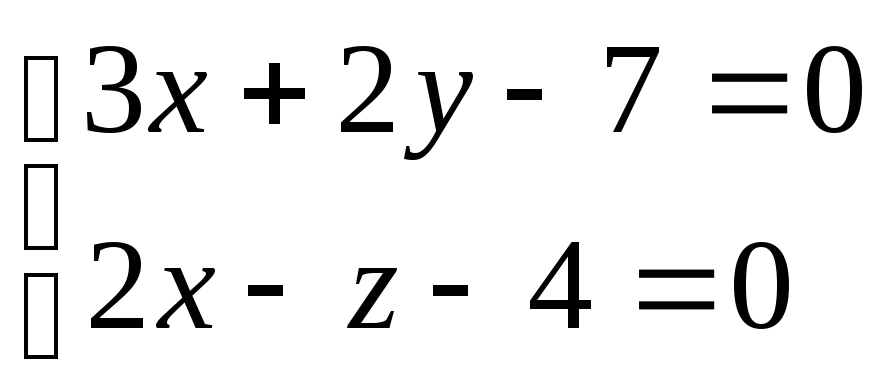Полученная система уравнений и есть общие уравнения прямой.

Рассмотрим переход от общих уравнений прямой к параметрическим и каноническим уравнениям прямой. Чтобы записать канонические или параметрические уравнения прямой, надо знать точку, через которую проходит прямая, и направляющий вектор прямой. Если определить координаты двух точек и, лежащих на прямой, то в качестве направляющего вектора м можно взять вектор. Координаты двух точек, лежащих на прямой, можно получить как решения системы уравнений, определяющих общие уравнения прямой. В качестве точки, через которую проходит прямая, можно взять любую из точеки. Проиллюстрируем сказанное выше на примере.

Пример.

Даны общие уравнения прямой

.

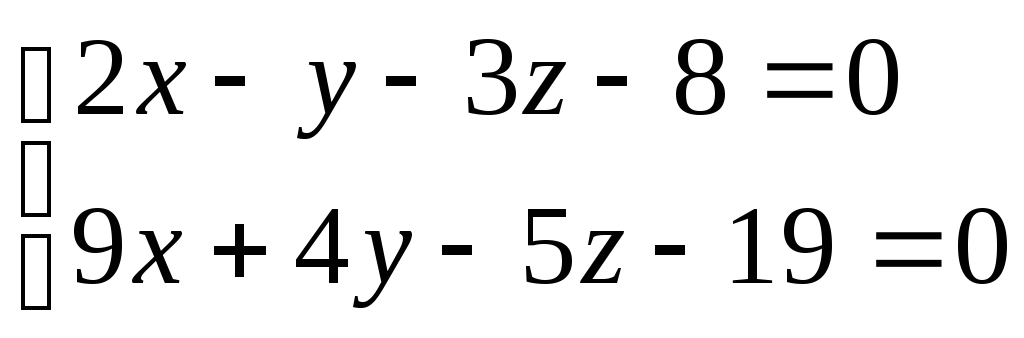Записать параметрические и канонические уравнения прямой.

Решение.

Найдем координаты двух точек, лежащих на прямой, как решения этой системы уравнений. Полагая , получим систему уравнений

.

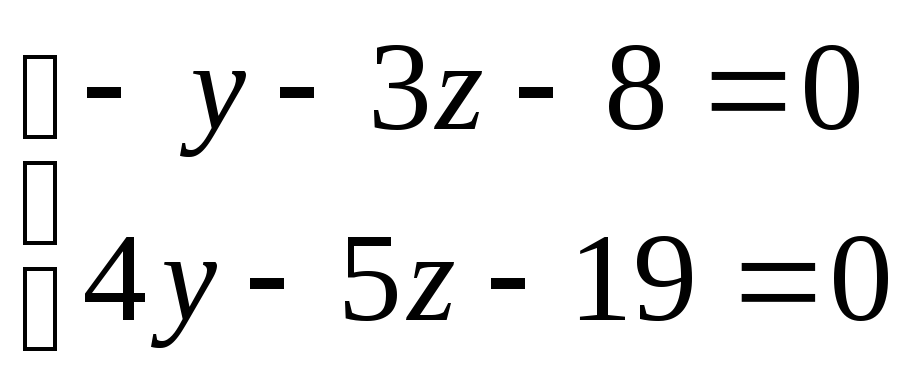Решая эту систему, находим . Следовательно, точкалежит на прямой. Полагая, получаем систему уравнений

,

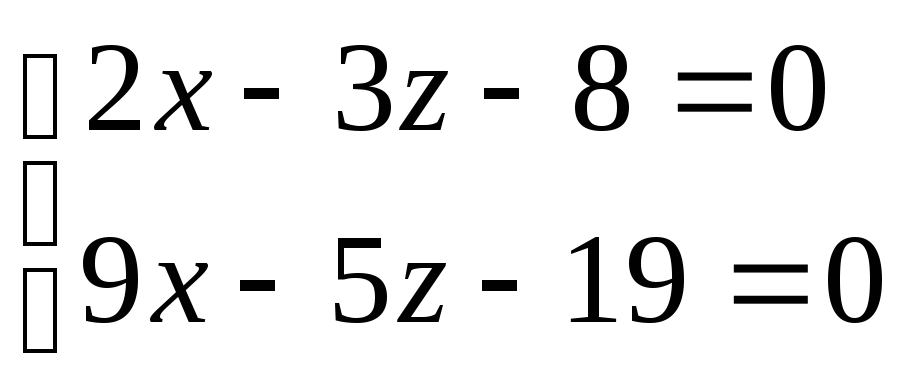решая которую находим . Следовательно, прямая проходит через точку. Тогда в качестве направляющего вектора можно взять вектор

.

Итак, прямая проходит через точку и имеет направляющий вектор. Следовательно, параметрические уравнения прямой имеют вид

.

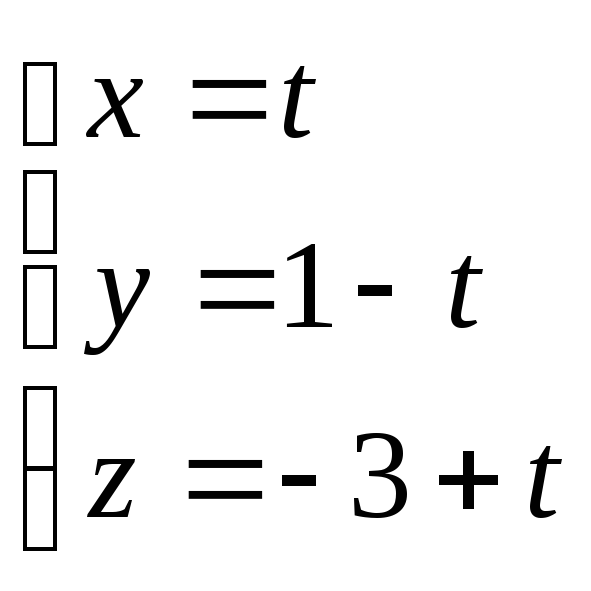Тогда канонические уравнения прямой запишутся в виде

.

Другой способ нахождения направляющего вектора прямой по общим уравнениям прямой основан на том, что в этом случае заданы уравнения плоскостей, а значит и нормали к этим плоскостям.

Пусть общие уравнения прямой имеют вид

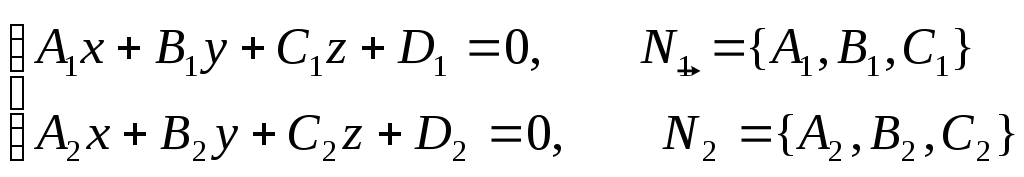
и- нормали к первой и второй плоскости, соответственно. Тогда векторможно взять в качестве направляющего вектора прямой. В самом деле, прямая, будучи линией пересечения этих плоскостей, одновременно перпендикулярна векторами. Следовательно, она коллинеарна векторуи значит этот вектор можно взять в качестве направляющего вектора прямой. Рассмотрим пример.

Пример.

Даны общие уравнения прямой

.

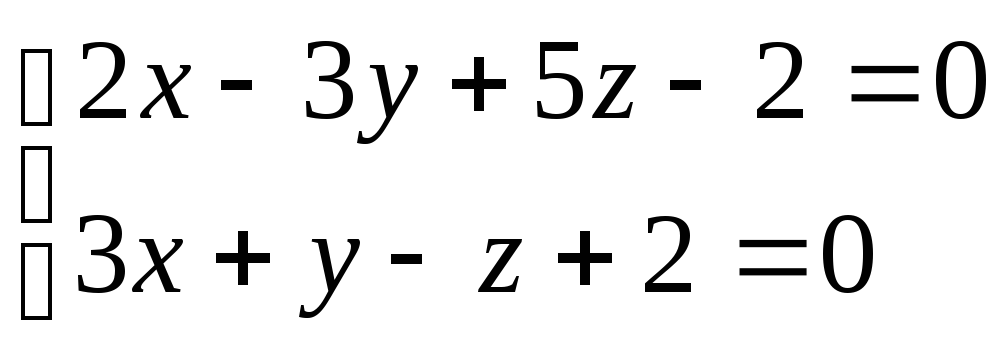Записать параметрические и канонические уравнения прямой.

Решение.

Прямая является линией пересечения плоскостей с нормалями и. Берем в качестве направляющего вектора прямой вектор

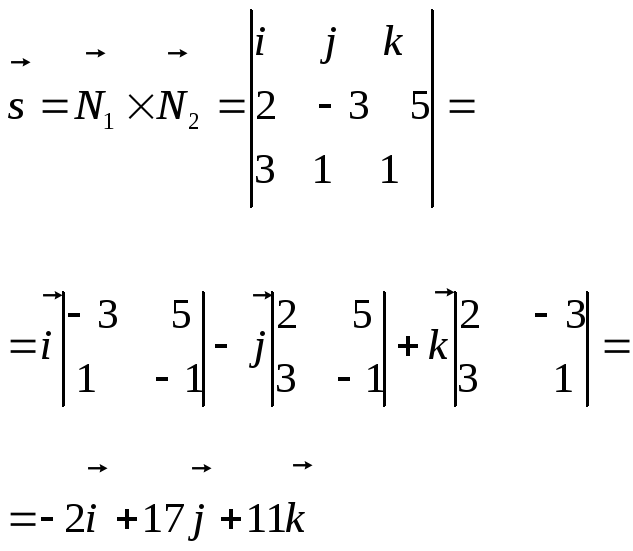
Найдем точку, лежащую на прямой. Найдем точку, лежащую на прямой. Пусть . Тогда получаем систему

.

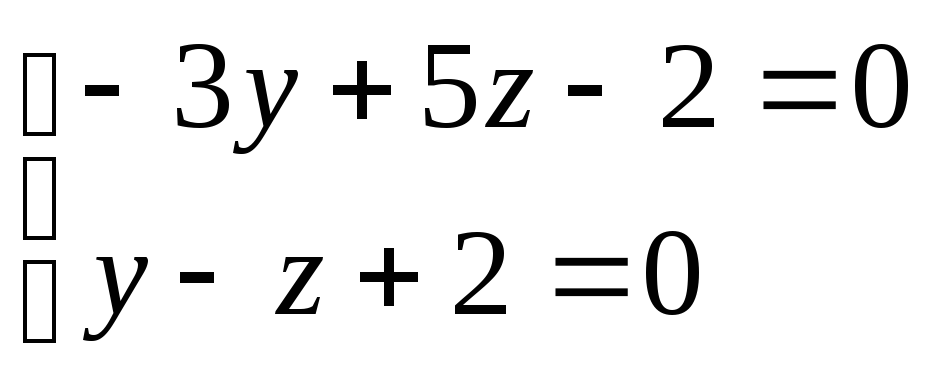Решая систему, находим .Следовательно, точкалежит на прямой. Тогда параметрические уравнения прямой можно записать в виде

.

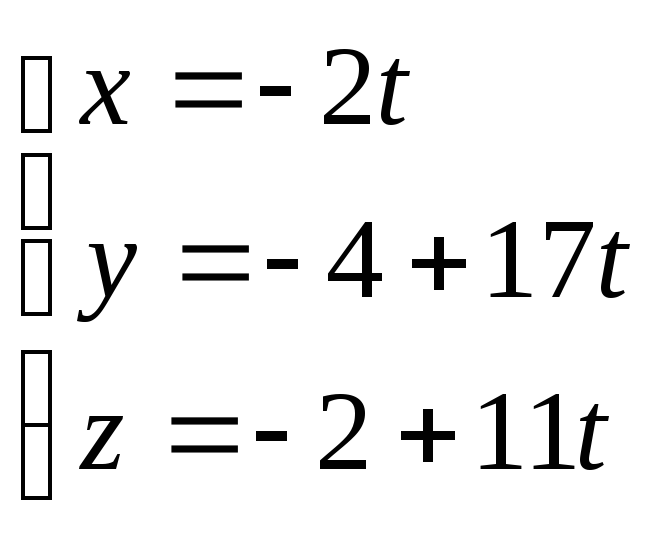Канонические уравнения прямой имеют вид

.

Наконец, к каноническим уравнениям можно перейти исключив в одном из уравнений одну из переменных, а затем другую переменную. Рассмотрим этот метод на примере.

Пример.

Даны общие уравнения прямой

.

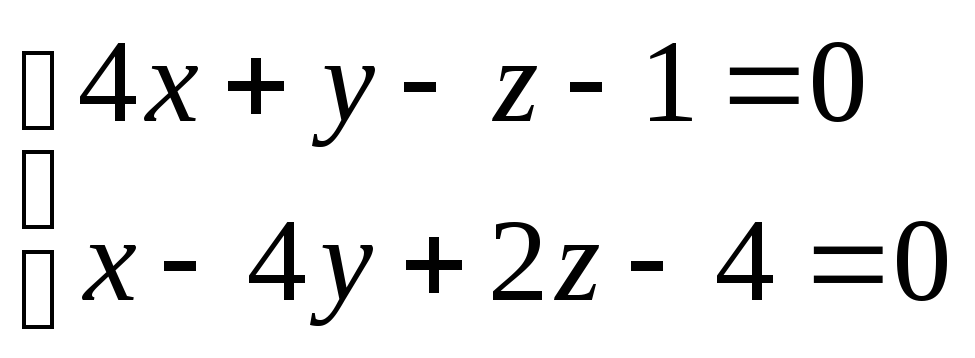Записать канонические уравнения прямой.

Решение.

Исключим из второго уравнения переменную у, прибавив к нему первое, умноженное на четыре. Получим

.

Или

.

Теперь исключим из второго уравнения переменную , прибавив к нему первое уравнение, умноженное на два. Получим

.

Или

.

Отсюда получаем каноническое уравнение прямой

.

Или

.

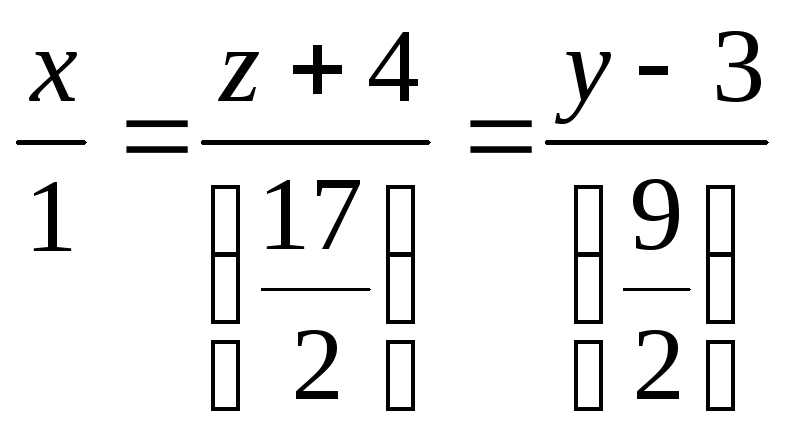Или

.