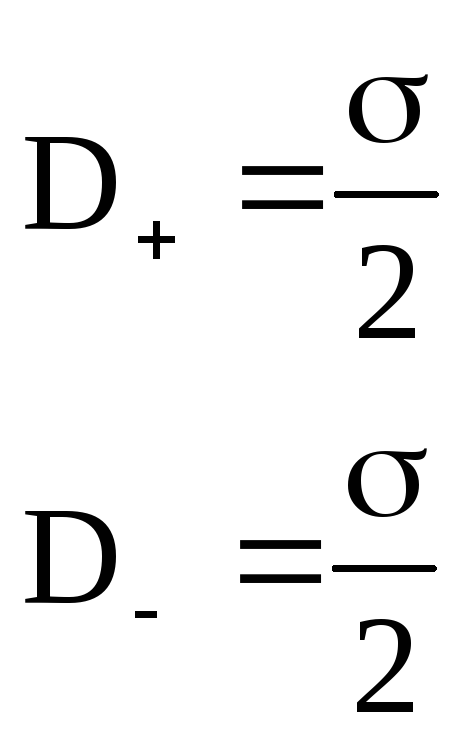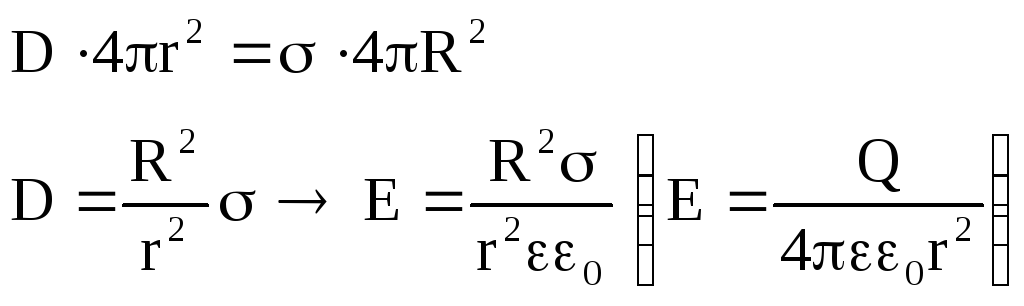Основы электростатики.

1. Закон Кулона. Напряженность электрического поля

Электростатика Учение о свойствах и взаимодействии электрических зарядов, неподвижных относительно избранной для них инерциальной системы отсчета [q]= Кл

Закон сохранения электрических зарядов Алгебраическая сумма электрических зарядов в замкнутой системе сохраняется постоянной

CИ: е = (1,601  0,001)10^-19 Кл

Закон Кулона.

, ,

Влияние не проводящей среды на величину электростатического взаимодействия между зарядами можно оценить, измерив силу взаимодействия в среде F и в ее отсутствии (в вакууме) F₀.

,

где  – диэлектрическая проницаемость среды.  > 1;  - безразмерная величина.

Закон Кулона в общем виде:

Если в пространстве обнаруживается действие сил на электрические заряды, то говорят, что в нем существует электрическое поле.

Электрическое поле изучают с помощью пробного точечного положительного заряда, величина которого своим действием заметно не искажает исследуемое поле..

Вектор напряженности электрического поля численно равен силе, действующей в данной точке на помещенный в нее пробный единичный положительный точечный заряд. – силовая характеристика электрического поля.

Используя закон Кулона можно получить:

Подчеркнем еще раз, что Q заряд создающий поле, а q – пробный заряд, используемый для исследования этого поля.

Напряженность электростатического поля не зависит от времени. Электростатическое поле называется однородным, если его напряженность во всех точках поля одинакова; в противном случае поле называется неоднородным.

Для графического изображения электростатических полей пользуются силовыми линиями. Силовыми линиями (линиями напряженности) называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке поля

Если электрическое поле создается несколькими зарядами q₁; q₂; q₃; …q_n, то результирующее поле будет действовать на пробный заряд с силой F, равной результирующей силе составляющих сил F_; F₂; F₃; …F_n.

Принцип наложения (суперпозиции) электрических полей:

Вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

2. Теорема Остроградского-Гаусса. А) плотность заряда

Если заряженное тело велико, то нужно знать распределение зарядов внутри тела.

Объемная плотность заряда – измеряется зарядом единицы объема:

Поверхностная плотность заряда – измеряется зарядом единицы поверхности тела (когда заряд распределяется по поверхности):

Линейная плотность заряда (распределение заряда вдоль проводника):

б) вектор электростатической индукции

Вектором электростатической индукции (вектором электрического смещения) называется векторная величина, характеризующая электрическое поле.

Вектор равен произведению векторана абсолютную диэлектрическую проницаемость среды в данной точке:

в) поток вектора электростатической индукции

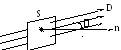N = Sdcosα = SD_n,

где N – поток вектора электростатической индукции, численно равный полному числу линий электрической индукции через эту поверхность

2. Если поле неоднородно, то поверхность разбивают на бесконечно малые элементы dS, которые считают плоскими и поле возле них однородным. Поэтому поток через элемент поверхности равен: dN = D_ndS,

а полный поток через любую поверхность:

N имеет размерность электрического заряда. Для общего случая, когда поле создается n точечными зарядами:

Теорема Остроградского-Гаусса Поток вектора электростатической индукции через любую замкнутую поверхность численно равен алгебраической сумме находящихся внутри этой поверхности зарядов

Теорема позволяет найти поток вектора электростатической индукции через замкнутую поверхность, внутри которой находятся электрические заряды, частности Q.

Рассмотрим примеры применения теоремы:

А.Равномерно заряженная плоскость.

Плоскость бесконечная, равномерно заряженная с поверхностной плотностью . Линии индукции  поверхности и по обе стороны.

В

N = 2DS

качестве замкнутой поверхности выберем прямой цилиндр, тогда поток через боковую поверхность цилиндра равен 0 ( = 90). Тогда полный поток сквозь цилиндр равен сумме потоков через основания:

(9)

Учитывая теорему Остроградского-Гаусса, что поток равен полному заряду, заключенному внутри цилиндра:

N = σS (10)

Решая (9) и (10):

2Ds = σS

тогда:

Б. Поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноименными зарядами (плоский конденсатор).

Тогда Вне пластин Dвн = 0

Вывод: Поле сосредоточено внутри конденсатора.

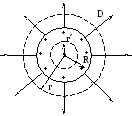
В. Поле, создаваемое заряженной сферической поверхностью.

Сферическая поверхность радиуса R с поверхностной плотностью σ+. Выделим мысленно поверхность радиуса r > R, тогда поток вектора электростатической индукции N равен: (D = Dn, т.к. силовые линии  поверхности). Согласно теореме Остроградского-Гаусса:

Согласно теореме Остроградского-Гаусса:

если r >> R: r = R :

r  R : E = 0 (т.к. зарядов внутри сферы радиуса r < R нет. Q =0 )

Г. Поле, создаваемое бесконечно длинной равномерно заряженной нитью.

Проведем коаксиальную цилиндрическую поверхность радиуса r. Поток через боковую поверхность цилиндра: N = DS = D·2πrℓ Поток по теореме Остроградского-Гаусса: N = Q = τℓ