Лекция №12. Электрические явления в проводниках и полупроводниках.

I.Классическая теория электропроводности металлов.

Что является носителем тока в металлах? Электроны или ионы?

Опыт Рике:

Через три цилиндра в течение года пропускается ток – по цепи прошло 3,5·106 Кл. Взвешивание цилиндров до и после опыта Al показало, что масса цилиндров const (с точностью до 3·10-5 г). Вывод: переноса вещества нет, ионы в проводимости не участвуют.

В 1913г. Мандельштамом и Папалекси была высказана идея опытов на инерционность подвижных носителей тока. Идея опытов осуществлена в 1916г. Толменом и Стюартом.

Опыт Толмена:

Катушка с медной проволокой приводилась во вращение со V = 300 м/с. При резком торможении гальванометр давал отброс. Действия магнитного поля Земли устранялось. Вывод: 1. Частицы, создающие ток, отрицательно заряжены (по направлению отклонения). 2. Определили – установили – электрон ,

где е и m –заряд и масса электрона;

V – скорость движения проводника;

R – сопротивление проводника;

q – заряд, прошедший через катушку.

Эти и ряд других опытов подтверждают положения электронной теории металлической проводимости (П. Друде, Г. Лорентц, А. Зоммерфельд) и подтверждают представление о строении металлического проводника: кристаллическая решетка состоит из положительных ионов, между которыми перемещаются электроны проводимости.

Объяснение различных свойств вещества существованием и движением в нем электронов составляет содержание электронной теории.

В электронной теории электроны проводимости рассматривают как электронный газ, подобный идеальному атомарному газу молекулярной физики (нет взаимодействия между электронами, взаимодействия электронов с ионами только соударением).

Т.к. свободный электрон обладает тремя степенями свободы, то средняя энергия теплового движения на один электрон равна:

Такая постановка даёт возможность объяснить многие электрические явления:

1) Электрическое сопротивление проводника.

При взаимодействии электронов с ионами решетки, последние испытывают соударения с ними, проходя путь между последовательными соударениями, равный – средней длине свободного пробега.

Число ударов, испытываемых одним электроном в единицу времени:

Чем больше , тем больше и R.

Среднее время между соударениями:

(1)

2) Закон Ома.

Считаем, что при каждом соударении электрон передает решетке накопленную энергию полностью и после соударения движется без начальной скорости.

Вычислим плотность тока в металле под действием поля Е:

, (2)

где – средняя скорость упорядоченного движения.

Сила, действующая на электрон:

,

где V_т – максимальная скорость в конце λ, следовательно, средняя скорость:

– среднее время между соударениями,

Итак, имеем:

Подставляя τ из уравнения (1), получим:

(3)

Зная что , где

b – подвижность,

имеем:

Подставляя в уравнение (2) получим:

, откуда:

(закон Ома)

j = γE,

где j – удельная электропроводность.

Вывод: 1) γ тем больше, чем больше n и ;

2) при увеличении Т, а, следовательно, и , сопротивление R увеличивается.

3) Закон Джоуля - Ленца.

Вывод из предположения, что вся Е_к, приобретенная электроном при прохождении λ, передаётся решетке при соударении и переходит в тепло.

4) Связь между электропроводностью γ и теплопроводностью æ металлов.

Однимиз выводов электронной теории являетсяустановление связи между γ иæ. Обладая энергиейтеплового движения 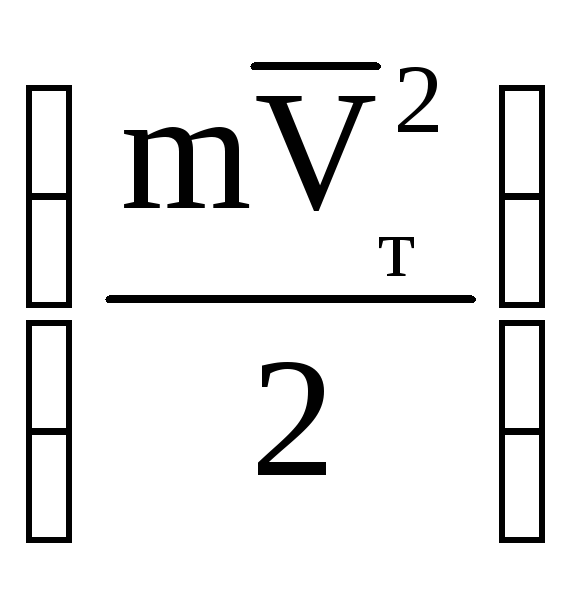, электроны переносяттепло в металле, и чем выше n, от которой зависит γ(γ ~ n²) и Н, тем вероятнее связь γ сæ. Она установленаВидеманом и Францем экспериментально:

,

где – const и не зависит от металла

Однако существуетряд явлений, находящихся в противоречии с электронной теорией:сверхпроводимость и теплоёмкостьметаллов.

Объяснение этих явлений, разрешившее расхождение результатов измерений и электронной теории, является применение квантовой статистики Ферми – Дирака, согласно которой:

даёт хорошее согласие с опытом,

где k – постоянная Больцмана.