Округление, функции floor() и ceil()

В этом разделе мы будем иметь дело исключительно с числами в формате с плавающей запятой. Во всех случаях, когда необходимо выполнить любую математическую операцию над числами с плавающей запятой, следует помнить об ограничениях, связанных с представлением этих чисел компьютером.

Компьютеры оперируют с числами только в двоичном формате, то есть с основой 2. В числах с основой 2 присутствует только две цифры - 0 и 1. Это идеальная система исчисления для компьютеров, поскольку значение 0 и 1 могут быть представлены простым двух-позиційним переключателем. Электролампочка, тумблер, електросхеми на лампах или транзисторах - все это примеры двухпозиционных переключателей.

Превращение целых чисел, представленных на базе двоичной основы, к формату с другой основой является относительно простой процедурой, которой занимаются компьютеры и неплохо производятся с момента их появления. При изменении основы числа не теряется ни "капле" информации., то есть при превращении целых чисел из одной системы в другую потери точности не происходит.

Но это утверждение справедливо только для целых чисел. Все мінюється, стоит только вставить в число десятичную кому. Способы, с помощью которых в компьютерах осуществлялось представление чисел с плавающей запятой, исторически были разнообразными, сложными и достаточно противоречивыми. Только в течение последних нескольких лет появилось что-то похожее на стандарт представления чисел этого типу. Однако многие считают, что даже этот стандарт, IEEE - 64, полный ловушек и недостатков. К сожалению, чтобы полностью раскрыть эту увлекательную тему, понадобится написать отдельную книгу не меньшего объема, чем данная. Но вряд ли такая книга выйдет, поскольку найдется не много людей, которые проявили бы к ней интерес. Уж слишком этот специфический вопрос для узкого круга специалистов. Пока вполне достаточно будет сообщить вам, что проблем в этом вопросе множество, а их решение связано со значительными трудностями.

На этом этапе вам достаточно знать, что при работе с числами с плавающей запятой возникают проблемы, связанные с потерей точности. Причем достаточно неожиданным оказывается тот факт, что умножение и деление при таких обстоятельствах сопровождается определенной погрешностью, которая умеренно растет при повторных операциях, тогда как повторное складывание и вычитание погрешность увеличивают существенно. Из этого выходит мораль - необходимо с осторожностью использовать складывание и вычитание чисел с плавающей запятой, а из двух способов решения задачи выбирать тот, где умножение и деление преобладают над суммированием и вычитанием.

Когда появляется необходимость производить математические действия с числами с плавающей запятой, рано или поздно возникает потребность превратить некоторые результаты, представленные в формате числа с плавающей запятой, в целые числа или в длинные целые числа. Для выполнения этого задания в Python есть простой способ, который заключается в том, чтобы использовать встроенные функции превращения типов. Несколько примеров их приложения показано на рис. 3.11.

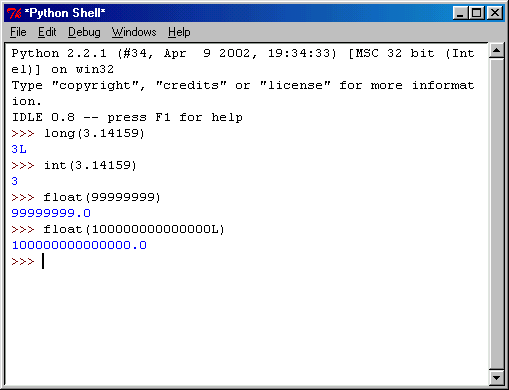
Рис. 3.11. Несколько примеров превращения типов

Превращения типов часто сопровождаются округлением значений. Иногда требуется округлить результат к большему значению, иногда - к меньшему. Для этого существуют специальные методы округления, которые позволяют контролировать эту операцию, : floor() и ceil().

Взвесим, что эти и целый ряд других операций (функций), находятся в специальном модуле с именем math. Там же находятся и наиболее употребляемые математические константы, например pi (3.141592..) и, чтобы ими воспользоваться, надо выполнить специальную операцию импортирования модуля из внешней памяті в память компютера, например

Рис. 3.12. Функции floor() и ceil()

Инструкция импортирования

from math import *

позволяет обращаться к членам модуля непосредственно, без указания имени модуля.

Существует и другая форма импорта, которая позволяет увидеть весь состав модуля, :

>>> import math

Нажмите на клавишу ENTER и наберите

>>> math.

((с точкой без нажатия ENTER).

В выпадающем списке вы увидите все, что входит в модуль math. Однако, чтобы вызывать число л (пи), нам пришлось бы вводить math.pi. Так же для обращения к функциям

floor() и ceil()

пришлось бы использовать вызовы

math.floor() и math.ceil().

Что удобнее, каждый программист решает в каждом конкретном случае сам.

На рис. 3.12 показано практически все, что необходимо знать для правильного использования функций округления и превращения типов. Только проверьте, чтобы количество открывающих круглых скобок отвечали количеству тех, которые закрывают. И еще на один момент хотелось бы обратить ваше внимание. Посмотрите, как функция long () принимает как аргумент другую функцию ceil (). Это важный момент, который необходимо хорошо запомнить,: вместо чисел как аргументов функций допускается использовать другие функции, которые обрабатывают свои аргументы.

Может возникнуть еще один вопрос, связанный с округлением чисел с плавающей запятой, - как будут округляться негативные числа? Мы ненадолго отложим обсуждение этого вопроса и вернемся к нему позже в этой главе.