для первого курса / для первого курса / тер мех / 12. Координатный способ задания движения

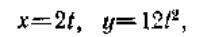
К о о р д и н а т н ы й способ з а д а н и я движения точки. Положение точки можно непосредственно определять ее декартовыми координатами х, у, z , которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т. е. ее положение впространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

(3)

Уравнения (3) представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за плоскость Oxy, получим в этом случае два

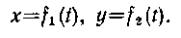(4)

Наконец, при прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением (законом прямолинейного движения точки)

(5)

Уравнения (3) и (4) представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время t, можно найти уравнение траектории в обычной форме, т. е. в виде, дающем зависимость между координатами точки.

Определение скорости точки. Вектор скорости точки v=dr/dt. Отсюда на основании формул (И), учитывал, что rx=x, ry=y, rz=z, найдем:

(12.1)

или

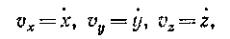(12.2)

где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции, скорости точки на координатные оси равны первым производным от соответствующих координат течки по времени.

Зная проекции скорости, найдем ее модуль и направление (т. е. углы α, β, γ которые вектор v образует с координатными осями) по формулам

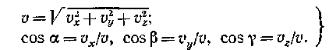.(13)

Определение ускорения точки. Вектор ускорения точки a=dv/dt. Отсюда на основании формул получаем:

(14)

или

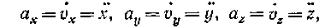
т. е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

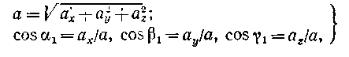(15)

где α1, β1, γ1 — углы, образуемые вектором ускорения с координатными осями.

Итак, если движение точки задано в декартовых прямоугольных координатах уравнениями, то скорость точки определяется по формулам (12) и (13), а ускорение— по формулам (14) и (15). При этом в случае движения, происходящего в одной плоскости, во всех формулах должна быть отброшена проекция на ось z.

В случае же прямолинейного движения, которое задается одним уравнением x=f{t), будет

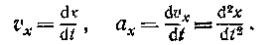(16)

Равенства (16) и определяют значения скорости и ускорения точки в этом случае.