2.3. Математическая модель затрат на передачу мощности по лэп.

Определение: типовая группа ЛЭП – это группа ЛЭП одной конструкции, с проводниками одного материала, но разного сечения.

Поставим задачу определения ежегодных приведенных затрат на типовую группу ЛЭП в зависимости от передаваемой по ЛЭП мощности S (рис2.4).

Рис.2.4. Определение затрат на передачу мощности S.

Ежегодные приведенные затраты на ЛЭП сечением F определяются по формуле (2.1.1): .

Первое слагаемое в этой формуле – это ежегодные отчисления от капитальных затрат на ЛЭП, не зависящие ни от сечения, ни от мощности. Например, для воздушной ЛЭП – это стоимость земли под ЛЭП, опор, изоляторов и т.п.

Второе слагаемое - это ежегодные отчисления от стоимости проводов, они прямо пропорциональны сечению, но не зависят от мощности.

Третье слагаемое – это стоимость годовых потерь электроэнергии в ЛЭП, пропорциональная квадрату мощности и обратно пропорциональная сечению.

На рис.2.5.а приведены графики затрат на передачу мощности по типовой группе ЛЭП. В интервале мощности 0 – S₁ минимум затрат будет обеспечен при использовании сечения F₁, в интервале S₁ – S₂ – при использовании сечения F₂ и так далее. Интервалы изменения мощности 0 – S₁, S₁ – S₂ и т.д., в которых минимум затрат имеет место при одном определенном сечении, называются экономическим интервалами. Границы экономических интервалов – это точки пересечения кривых затрат, соответствующих разным сечениям проводов.

Рис. 2.5. Точная математическая модель затрат на передачу мощности по ЛЭП.

График точной математической модели затрат на ЛЭП приведен на рис.2.5.б – это нижняя огибающая семейства кривых затрат, изображенных на рис. 2.5.а.

Точная математическая модель – это кусочно-гладкая квадратичная функция от мощности, границы излома которой соответствуют границам экономических интервалов. Недостатком точной модели является ее сложность, которая может быть устранена линеаризацией. Для перехода к линейной модели делается допущение о непрерывности шкалы сечений, т.е. предполагается, что, например, между стандартными сечениями F₁ и F₂ имеется еще множество промежуточных сечений. Тогда набор отрезков кривых заменяется касательной к этим отрезкам прямой линией (рис.2.6).

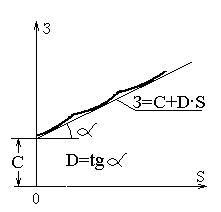
Рис.2.6. Линейная математическая модель затрат.

Для получения аналитического выражения линейной математической модели в точную формулу затрат (2.1.1) подставим выражение экономического сечения

(2.2.1)

.

Обозначим

, тогда

2.4. Расчет сечения по допустимой потере напряжения.

После расчета и выбора сечения ЛЭП по нагреву (сети ниже 1000 В) или по экономической плотности тока (сети выше 1000 В) производится проверка по токам КЗ и на допустимую потерю напряжения ΔU ≤ ΔU_ДОП. Если эта проверка дает отрицательный результат (ΔU > ΔU_ДОП), то нужно определить сечение, при котором потеря напряжения будет равна допустимой ΔU = ΔU_ДОП, т.е. сделать расчет сечения по допустимой потере напряжения.

Допустим имеется магистральная ЛЭП 6-35 кВ, состоящая из «n» участков

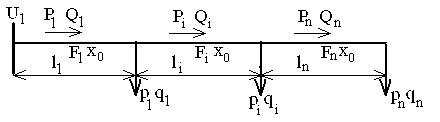
Рис.

Потеря напряжения в ЛЭП:

, где (2.4.1)

- удельная проводимостьматериала проводников.

Учитывая, что удельное индуктивное сопротивление х₀ слабо зависит от сечения, можно принять его неизменным х₀ = Const и известным (на уровне среднего значения). Тогда реактивная составляющая потери напряжения:

. (2.4.2)

Далее при известной величине ΔU_ДОП можно определить допустимую (располагаемую) активную составляющую потери напряжения:

, или:

. (2.4.3)

Это уравнение содержит “n” неизвестных F₁… F_i …F_n и, следовательно, имеет множество решений. Поэтому для нахождения одного решения необходимо наложить дополнительные условия. Ими могут быть:

а) Одно сечение на всех участках ЛЭП, F = Const;

б) Минимум расхода проводникового материала;

в) Одинаковая плотность тока на всех участках ЛЭП, j = Const.

Условие а: одинаковое сечение по всей длине магистрали.

Перепишем формулу (2.4.3), вынося постоянные члены за знак суммы:

, где F = Const, откуда

. (2.4.4)

Благодаря удобству монтажа и эксплуатации ЛЭП, имеющей одинаковые провода на разных участках, на практике это решение используется часто. К недостаткам этого решения относятся повышенные расходы на потери электроэнергии на перегруженных головных участках ЛЭП и на провода завышенного сечения конечных участков.

Условие б: минимум расхода проводникового материала.

Вывод формулы расчета сечения удобно сделать на примере магистральной ЛЭП, состоящей из двух участков (рис. ).

Рис.

Потеря напряжения на реактивных сопротивлениях участков ЛЭП:

;

Допустимая потеря напряжения на активных сопротивлениях участков ЛЭП:

.

. (2.4.5)

Потери напряжения на активных сопротивлениях участков 1 и 2:

, . (2.4.6)

Потеря напряжения на втором участке:

.

Сечения проводов на участках 1 и 2 из формул (2.4.6):

.

Далее запишем выражение для объема трех проводов ЛЭП:

.

Объем проводов зависит от распределения потерь напряжения по участкам 1 и 2, то есть от ΔU_a1. Для нахождения минимума объема нужно первую производную от V по ΔU_a1 приравнять к нулю:

, или:

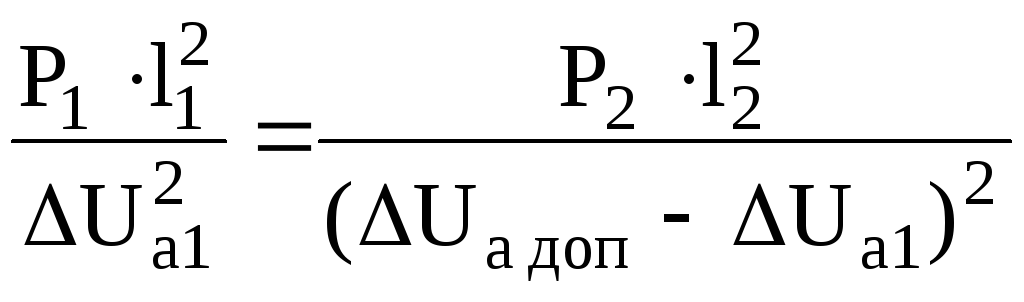. Вместо ΔU_a1 и ΔU_a2 подставим их значения (2.4.6):

.

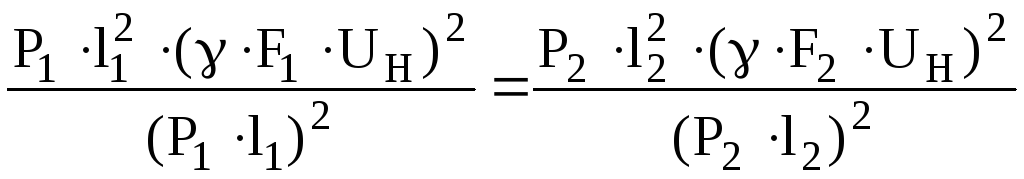После упрощений получаем важное соотношение сечений и мощностей участков ЛЭП: . (2.4.7)

Сечение проводов разных участков должно изменяться пропорционально корню квадратному из мощности.

Например, Р₂ =1, F₂ =1, Р₁ = 2, F₁ = √2 = 1,41. Мощность, передаваемая по первому участку вдвое больше мощности первого участка, а сечение первого участка лишь в 1,41 раз больше сечения второго участка.

Далее, используя (2.4.7), выразим F₁ через F₂:

и подставим его в (2.4.5):

.

После упрощений получаем:

, откуда находим сечение F₂:

откуда находим сечение F₂:

.

Если ЛЭП состоит не из двух, а из «n» участков, то сечение последнего (n-го) участка запишется:

. (2.4.8)

Зная сечение последнего участка, можно найти сечение любого другого, используя выражение (2.4.7):

.

Условие в: постоянная плотность тока.

Для ЛЭП, состоящей из «n» участков запишем формулу допустимой потери напряжения:

.

Считая реактивное сопротивление известным, определяем потерю напряжения на нем:

и допустимую потерю напряжения на активном сопротивлении:

,

. (2.4.9)

В последнем выражении (2.4.9) отношение - это плотность тока на участке “i”, одинаковая на всех участках.

Вынесем постоянные величины за знак суммы:

, откуда:

и (2.4.10)

.

Если плотность тока, полученная с помощью выражения (2.4.10) значительно меньше экономической плотности для данного типа ЛЭП, то это свидетельствует о неправильном выборе номинального напряжения ЛЭП: оно занижено.