4.1. Определения

Падение напряжения – это геометрическая разность напряжений в начале и конце ЛЭП. Падение напряжения – это векторная величина.

Потеря напряжения – это алгебраическая разность тех же напряжений в начале и конце ЛЭП. Потеря напряжения – это скалярная величина.

Отклонение напряжения (отклонение от номинального значения) – это алгебраическая разность между фактическим напряжением в данный точке сети и номинальным этой же точке сети, при медленном его изменении:

Колебания напряжения – при быстром изменении (>1% в сек.).

В общем случае потеря в ЛЭП складывается из потерь в прямом и обратном проводах. Но в 3-х фазной ЛЭП с симметричной нагрузкой потеря напряжения в обратном проводе отсутствует, т.к. ток в нем (в нейтральном проводе) равен нулю.

4.2. Падение и потеря напряжения в 3-х фазной лэп с симметричной нагрузкой

На схеме замещения одной фазы электропередачи, приведенной на рис. 4.1:

r – активное сопротивление провода ЛЭП.

х – реактивное сопротивление провода.

z_н – комплексное сопротивление нагрузки (характеризуется углом φ).

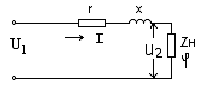
Рис. 4.1. Схема замещения одной фазы электропередачи.

Считаем - известно. Построим векторную диаграмму и найдем вектор(рис. 4.2).

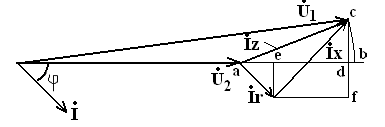
Рис. 4.2. Векторная диаграмма электропередачи.

ас – падение напряжения.

аb – потеря напряжения.

На практике отрезок ad считают потерей напряжения, пренебрегая отрезком db.

- продольная слагающая падения напряжения (потеря).

,

.

- фазная потеря напряжения.

- линейная потеря. Умножим и разделим на Uн:

.

Поперечная слагающая падения напряжения изображается отрезком cd:

- поперечная слагающая падения напряжения.

Модуль вектора напряжения в начале ЛЭП определяется по теореме Пифагора:

В расчетах распределительных сетей (сетей среднего 6-35 кВ и низкого напряжений) обычно учитывают только продольную составляющую напряжения.

4.3. Расчет потери напряжения в ответвлениях от 3-х фазной лэп

В трехфазном ответвлении с симметричной нагрузкой , поэтому потеря напряжения в контуре одной фазы (например В):

а). Двухфазное ответвление:

Рис. 4.3. Двухфазное ответвление от трехфазной ЛЭП.

Нагрузки фаз активны и равны между собой:иI_B = I_C..

Сечение проводов невелико, , поэтому- не учитывается.

- сечения и длины фазных и нейтрального проводников одинаковы.

Рис. 4.4. Построение вектора тока в нейтральном проводе и определение потери ΔU_B.

Фазное напряжение U_В в начале ответвления по второму закону Кирхгофа:

,

.

Модули токов Ib и IN равны: Ib = IN, сопротивления r_B = r_N также равны.

Потеря напряжения в контуре фазы В (рис.4.4):

Однофазное ответвление (рис. 4.5).

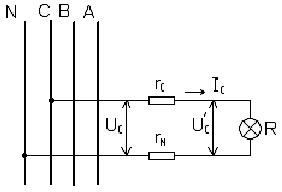
Рис. 4.5. Однофазное ответвление.

Потеря напряжения: .

При прочих равных условиях потеря напряжения зависит от числа фаз ответвления:

- 3-х фазное ответвление – коэффициент 1 – самая малая потеря;

- 2-х фазное ответвление – коэффициент потери = 1,5;

- однофазное ответвление – коэффициент 2 – максимальная потеря.

4.4. Формулы потерь напряжения в 3-х фазной ЛЭП.

, Вольт;

С учетом размерностей величин, входящих в формулу: ,,:

.

Имеется ЛЭП постоянного сечения с несколькими нагрузками по длине (рис.4.6):

Рис. 4.6. ЛЭП С несколькими нагрузками по длине (магистральная ЛЭП).

Потеря напряжения в линии может быть определена исходя из мощностей отдельных участков P_i, Q_i и длин этих участков L_i, или мощностей нагрузок p_i, q_i и расстояний до источника питания l_i.

.

Если нагрузка равномерно распределена вдоль линии (рис.4.7), то для расчета потери напряжения ее считают сосредоточенной в середине нагруженного участка.

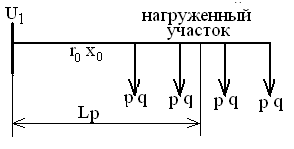
Рис.4.7. ЛЭП с нагрузкой, равномерно распределенной по длине.

Тогда ,где Рр = ∑ р_i , Qp = ∑ q_i.

В маломощных сетях напряжением ниже 1000 В часто и/или. В этом случае произведениемQ·x можно пренебречь и формула потери напряжения приобретает следующий вид:

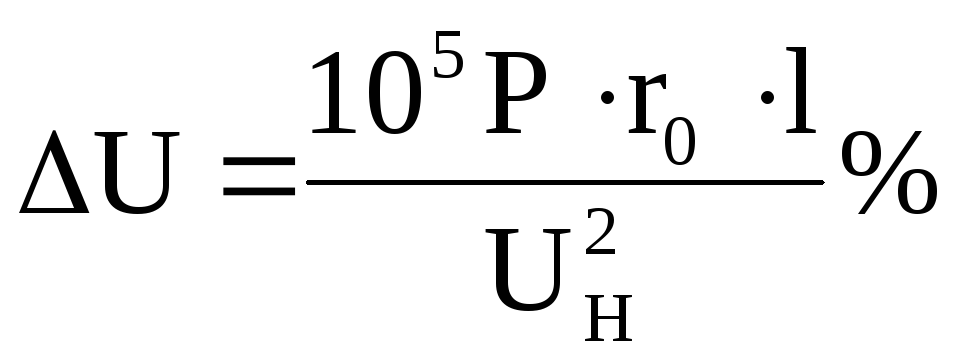, где

- удельное активное сопротивление проводников.

- длина ЛЭП.

На практике часто используется формула потери напряжения через момент мощности:

, где

- момент нагрузки (момент мощности),

- сечение.

;

- коэффициент зависящий от количества фаз, материала проводов и напря­же­ния сети. Например, для 3-х фазной сети, провода из алюминия, напряже­ние 380/220 В: .

Для однофазной сети 220 В , т.е в 6 раз меньше, чем для трехфазной:

мощность в 3 раза меньше, а потеря напряжения – в 2 раза больше из-за

дополнительной потери и в нейтральном проводе. Итого 3·2 = 6.