
- •Исследование скважин, оборудованных штанговыми насосными установками.
- •Коэффициент подачи штангового скважинного насоса. Постоянные и переменные факторы, влияющие на коэффициент подачи штангового скважинного насоса.
- •Минимальное забойное давление фонтанирования. Определение глубины начала выделения газа.
- •Нагрузки, действующие на штанги и их влияние на ход плунжера.
- •Назовите и объясните способы защиты погружного насоса от вредного влияния газа.
- •Напорная характеристика скважины. Распределение давления вдоль ствола скважины для жидкости и гжс.
- •Несовершенство скважин. Влияние несовершенства на дебит скважины. Формула дебита несовершенной скважины.
- •Формулы притока жидкости к несовершенным скважинам
- •Несовершенство по качеству вскрытия
- •Общая схема установки погружного центробежного электронасоса. Определение подачи насоса при некотором газосодержании на его приеме.
- •Опишите технологию определения положения динамического уровня жидкости в скважине. Цель и назначение.
- •Определение глубины подвески погружного электроцентробежного насоса.
- •Определение дебита фонтанной скважины. Минимальное забойное давление фонтанирования. (см.15?)
- •Определение подачи уэцн. Основные достоинства и недостатки уэцн.
-
Несовершенство скважин. Влияние несовершенства на дебит скважины. Формула дебита несовершенной скважины.
В теории фильтрации различают три вида несовершенства скважины:
-
скважина гидродинамически несовершенная по степени вскрытия пласта – это скважина с открытым забоем, вскрывшая пласт не на всю толщину;
-
скважина гидродинамически несовершенная по характеру вскрытия пласта – это скважина, вскрывшая пласт на всю толщину, но сообщающаяся с пластом через систему перфорационных отверстий или специальные фильтры;
-
скважина гидродинамически несовершенная как по степени, так и по характеру вскрытия.

Рис. 5.1. Схема притока к скважине, несовершенной по характеру вскрытия
- расстояние между отверстиями вдоль оси скважины;
rc- радиус гидродинамически несовершенной скважины.
Скважина, несовершенная по характеру вскрытия, сообщается с пластом через систему перфорационных отверстий. Вблизи отверстий форма потока радиально-сферическая. Суммарная площадь фильтрации определяется суммой сечений отверстий, что значительно меньше поверхности вскрытого пласта. Это приводит к возникновению дополнительных сопротивлений в призабойной зоне пласта. Исследования показывают, что за пределами цилиндрической поверхности радиуса R0 = rc+ линии тока практически параллельны, и поток становится плоскорадиальным.
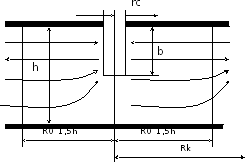
Рис. 5.2. Схема притока к скважине, несовершенной по степени вскрытия
Если скважина гидродинамически несовершенна по степени вскрытия. То линии тока будут параллельны за пределами цилиндрической поверхности радиуса R01,5h. В зоне, прилегающей к скважине, поток жидкости вблизи кровли пласта будет плоскорадиальным, а в остальной части – радиально-сферическим.
Формулы притока жидкости к несовершенным скважинам
Дебит скважины, несовершенной по степени вскрытия, можно найти по формуле Н.К.Гиринского, если считать, что скважина вскрыла пласт неограниченной толщины на глубину b:
 .
(5.1)
.
(5.1)
Для
пласта конечной толщины h
М.Маскет предложил формулу, при условии,
что
 :
:
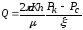 ,
(5.2)
,
(5.2)
где
 .
.
Здесь
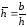 - относительное вскрытие пласта.
- относительное вскрытие пласта.
Иногда для расчета дебита скважины, несовершенной по степени вскрытия, используется более простая формула, чем формула М.Маскета, - формула И.Козени:
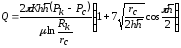 .
(5.3)
.
(5.3)
Для дебита скважины, вскрывшей пласт на малую глубину (bh), существует формула И.А.Чарного:
 .
.
Принимая R0=1,5h, окончательно имеем:
 .
(5.4)
.
(5.4)
Дебит скважины, сочетающей оба вида несовершенства, можно определить по формуле:
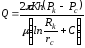 ,
(5.5)
,
(5.5)
где С=С1+С2 – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия (С1) и по характеру вскрытия (С2).
С – величина безразмерная.
Значения С1 и С2 находятся по графикам В.И.Щурова.
Формулу (5.5) можно записать в виде:
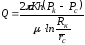 ,
,
где
 - приведенный радиус скважины, т.е. радиус
такой гидродинамически совершенной
скважины, дебит которой равен дебиту
данной несовершенной скважины.
- приведенный радиус скважины, т.е. радиус
такой гидродинамически совершенной
скважины, дебит которой равен дебиту
данной несовершенной скважины.
 .
.
Значения приведенного радиуса обычно составляют (10-210-4) м.
Иногда гидродинамическое несовершенство скважины учитывается при помощи коэффициента совершенства :
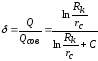 ,
,
где Q – дебит несовершенной скважины; Qсов – дебит совершенной скважины в тех же условиях.
