
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И
ПРИКЛАДНОЙ ИНФОРМАТИКИ
М.А. Евдокимов Л.Г. Волкова О.Н. Кузнецова
Определители и системы линейных уравнений
Учебное пособие для самостоятельной работы студентов
САМАРА
2008
Линейная алгебра
Определители и системы линейных уравнений
Определители 2го порядка
Пусть дана система двух линейных уравнений с двумя неизвестными.
 (1)
(1)
Решаем эту систему методом исключения неизвестных. Исключим у. Для этого первое уравнение умножаем наа22, второе на –а12, затем уравнения складываем, получаем после преобразований
![]() .
.
Если
![]() ,
то можем найтих
,
то можем найтих
![]() . (2)
. (2)
Число
![]() называется определителем 2гопорядка и обозначается
называется определителем 2гопорядка и обозначается
![]() .
.
Выражение, стоящее в числителе, тоже является определителем 2гопорядка
![]() .
.
Правило вычисления определителя 2го порядка
Сначала
об элементах определителя:
![]() .
.
 - элемент определителя, стоящий вi-ой
строке и вj-ом столбце,
- элемент определителя, стоящий вi-ой
строке и вj-ом столбце,i,j – индексы,
 - элементыi-ой строки,
- элементыi-ой строки, - элементыj-ого столбца,
- элементыj-ого столбца, - элементы главной диагонали,
- элементы главной диагонали, - элементы побочной диагонали.
- элементы побочной диагонали.
![]()




 .
.
Примеры:
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4)
![]() .
.
Аналогично методом исключения получим решение для у
![]() . (3)
. (3)
Видим, что структура формулы (3) такая же, что и у формулы (2), обозначив
![]() ,
,
получим формулы для решения системы

Это
формулы Крамера, они дают единственное
решение, если
![]() .
.
Пример.
Решить систему

1.
![]() Решение существует.
Решение существует.
2.
![]() .
.
3.
![]() .
.
4.
![]() ;
;![]() .
.
Формулы Крамера были получены из соотношений
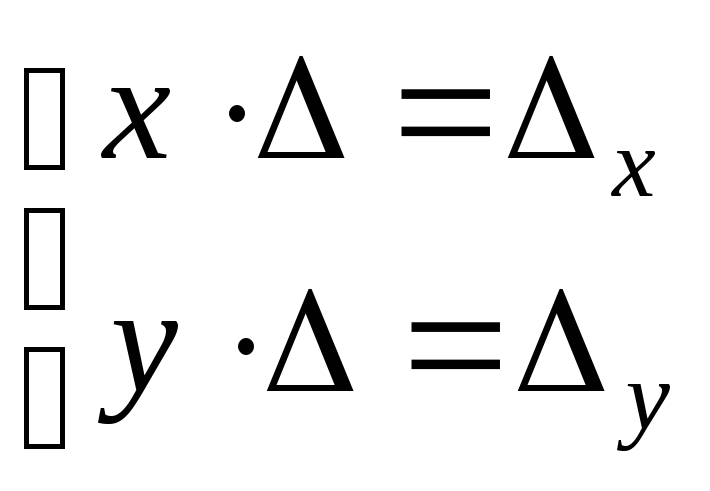 (4)
(4)
полагая, что
![]() .
Т.е.
.
Т.е.
![]()
или
![]() .
.
Значит система имеет единственное решение если ее коэффициенты непропорциональны. Говорят, что система определенна.
Если
![]() ,
но хотя бы один из определителей
,
но хотя бы один из определителей![]() или
или![]() отличны от нуля, то одно из равенств (4)
невозможно, и система не имеет решения.
Говорят, что системанесовместна.
отличны от нуля, то одно из равенств (4)
невозможно, и система не имеет решения.
Говорят, что системанесовместна.
Если
![]() ,
то это означает пропорциональность
коэффициентов системы
,
то это означает пропорциональность
коэффициентов системы
![]() .
.
Значит одно из уравнений получено из другого умножением на некоторое число т. И в действительности мы имеем одно уравнение с двумя неизвестными
![]() . (5)
. (5)
Такое уравнение имеет бесконечное множество решений, связанных с уравнением (5). Таким образом система совместна, но неопределенна.
Из (5)
найдем
![]() .
.
Если
обозначить
![]() ,
то
,
то![]() – можно и так записать решение.
– можно и так записать решение.
Рассмотрим выполнение заданий на вычисление определителей второго порядка и решение систем двух линейных уравнений с двумя неизвестными.
Задание 1
Вычислить определитель

Решение
Применяя формулу получим
 .
.
Ответ: Δ = 2.
Задание 2
Вычислить определитель
 .
.
Решение
Применяя формулу получим
 .
.
Ответ:
![]() .
.
Задание 3
Вычислить определитель
 .
.
Решение
Применяя формулу получим
 .
.
Ответ: Δ = 1.
Задание 4
Вычислить определитель
 .
.
Решение
Применяя формулу получим
 .
.
Ответ: Δ = cos2α.
Задание 5
При
каких значениях ![]() обращается в ноль определитель
обращается в ноль определитель
 ?
?
Решение
Применяя формулу вычислим данный определитель
 .
.
Следовательно,
Δ = 0 при a
=
![]() 2.
2.
Ответ:
a
=
![]() 2.
2.
Задание 6
Решить уравнение
 .
.
Решение
Применяя формулу вычислим данный определитель
 .
.
Следовательно, чтобы найти корни исходного уравнения, необходимо решить квадратное уравнение x2 – 8x +12 = 0:

Ответ: x1 = 6; x2 = 2.
Задание 7
При
каких значениях ![]() выполняется неравенство
выполняется неравенство
 ?
?
Решение
Применяя формулу вычислим данный определитель
 .
.
Получаем неравенство x2 – 6x + 7> - 1 или x2 – 6x + 8> 0. Квадратный трехчлен в левой части неравенства имеет корни x1 = 4 и x2 = 2. Следовательно, последнее неравенство можно записать в виде:
(x – 4)(x – 2)>0
Это неравенство выполняется для всех x>4 и x<2.
Ответ:
![]() .
.
Задание 8
Решить
систему

Решение
Вычислим определитель системы:
 .
.
Так как Δ = -5 ≠ 0, то система имеет единственное решение, которое можно найти по формулам Крамера:
![]()
Для этого вычислим определители Δ1 и Δ2:
 ;
;
 .
.
Следовательно,
![]()
Ответ: x1 = 3; x2 = -1.
Задание 9
Решить
систему

Решение
Вычислим определитель системы:
 .
.
Так как Δ = 0, то необходимо вычислить определители Δ1 и Δ2, чтобы решить вопрос о совместности системы.

Так как Δ1 = -14 ≠ 0, то система несовместна (не имеет решения).
Ответ: Система несовместна.
Задание 10
Решить
систему

Решение
Вычислим определитель системы:
 .
.
Так как Δ = 0, то необходимо вычислить определители Δ1 и Δ2, чтобы решить вопрос о совместности системы.
 и
и
 ,
,
потому что у этих определителей пропорциональны строки (свойство 6 определителей). Следовательно, система имеет бесчисленное множество решений.
Ответ: система имеет бесчисленное множество решений.
Следующее задание выполните самостоятельно.
Задание 11
Исследовать
систему уравнений

Если при решении Вы получили следующий ответ:
при
 система
имеет единственное решение
система
имеет единственное решение
![]()
при
 ,
,
 система имеет бесчисленное множество
решений.
система имеет бесчисленное множество
решений.при
 и
и  система несовместна,
система несовместна,
то Вы решили правильно. В противном случае рассмотрите решение данного задания.
Решение задания 11.
Вычислим определитель системы
 .
.
Так как Δ ≠ 0для все значений a, кроме a = -3, то система имеет единственное решение, которое можно найти по формулам Крамера:
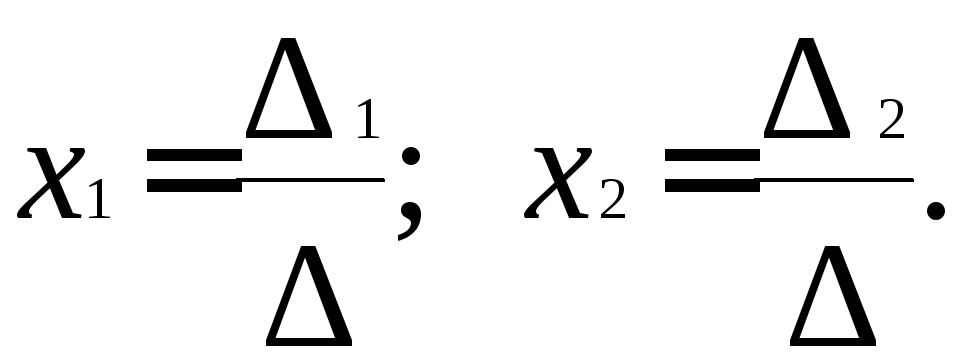
Для этого вычислим определители Δ1 и Δ2:
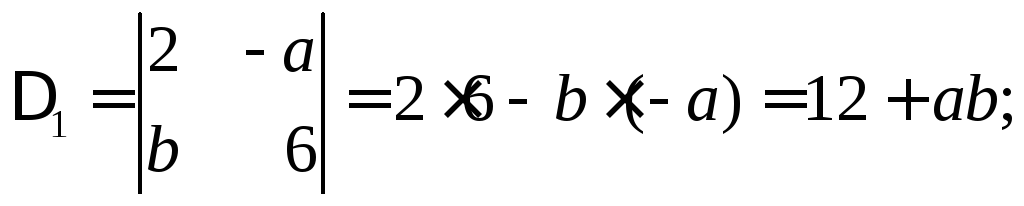
 .
.
Следовательно,
![]()
Если
![]() и
и ![]() ,
то
,
то ![]() ,
и система имеет бесчисленное множество
решений.
,
и система имеет бесчисленное множество
решений.
Если
же ![]() и
и ![]() ,
то
,
то ![]() ,
а
,
а
![]() и
и
![]() ,
т.е. система несовместна (не имеет
решений).
,
т.е. система несовместна (не имеет
решений).
Ответ:
при
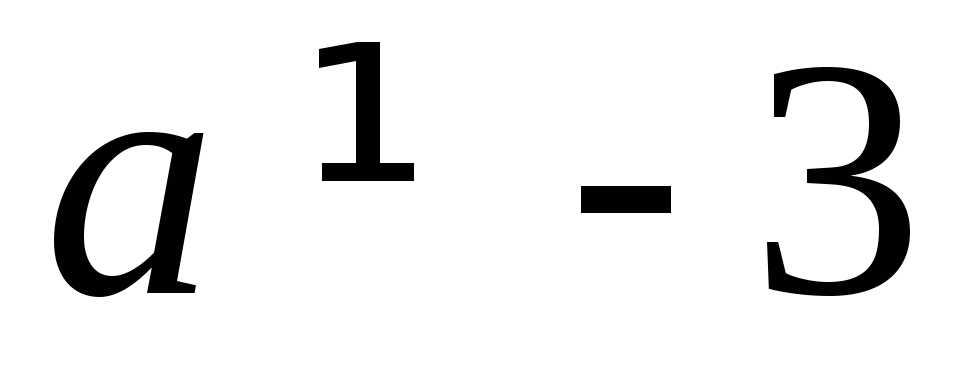 система
имеет единственное решение
система
имеет единственное решение
![]()
при
 ,
,
 система имеет бесчисленное множество
решений.
система имеет бесчисленное множество
решений.при
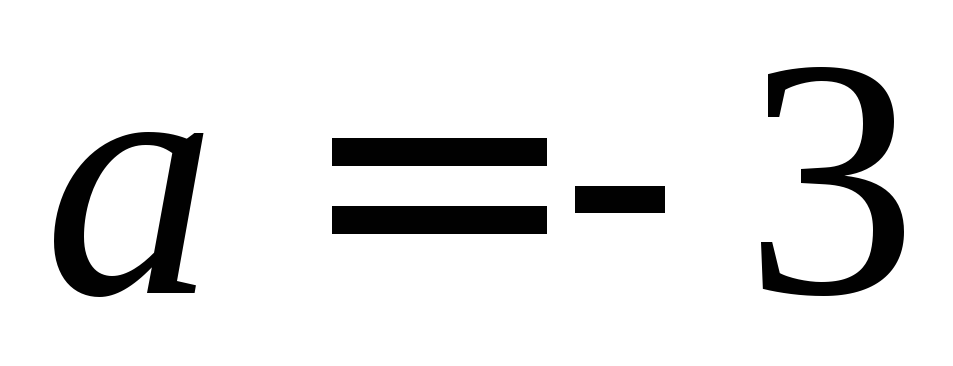 и
и  система несовместна.
система несовместна.
Определители 3го порядка
Определитель 3гопорядка есть число, зависимое и вычисляемое следующим образом:
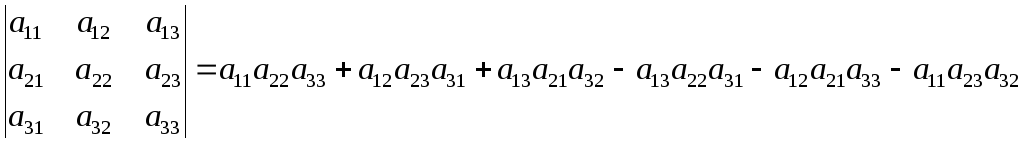 .
.
Для упрощения вычисления определителя имеется несколько схем.
Схема треугольников.

С


 хема
Саррюса
хема
Саррюса













Свойства определителей
Мы изучили свойства общие для определителей любого порядка. Но будем рассматривать их на примере определителя 3гопорядка.
1с) Величина определителя не изменится, если его строки и столбцы поменять местами.
Такая
операция называется транспонированием
определителя и обозначается
![]() ,
таким образом
,
таким образом
![]() .
.
Проверить
справедливость этого свойства можно
вычислением определителя
![]() и
и![]() .
.
 .
.
Это свойство говорит о равноправии строк и столбцов определителя с точки зрения его свойств.
2с) При перестановке 2хстрок (или столбцов) определитель меняет знак.
![]()

Проверка вычислением.
3с) Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Доказательство:
Предположим
![]() и определитель равен
и определитель равен![]() .
Переставим
.
Переставим![]() и
и![]() .
Согласно 2с) определитель должен сменить
знак, т.е. стать равным
.
Согласно 2с) определитель должен сменить
знак, т.е. стать равным![]() .
Но строки равны и перестановка не должна
сказаться на его величине, таким образом
.
Но строки равны и перестановка не должна
сказаться на его величине, таким образом
![]() ,
,
а это возможно, если
только
![]() .
.
4с) Общий множитель элементов строки (столбца) можно вынести за знак определителя.
Доказательство:
Предположим какая-либо строка, например 1ая, имеет общий множитель, значит все элементы с первым индексом 1 имеют этот общий множитель. А элементы с таким первым индексом входят в каждое произведение выражения для вычисления определителя. Значит этот множитель входит в каждое произведение и его можно вынести за скобки или за знак определителя.
 .
.
5с) Если все элементы некоторой строки (столбца) равны нулю, то определитель равен нулю.
Доказательство: вытекает из предыдущего свойства.
6с) Если соответствующие элементы 2хстрок (столбцов) пропорциональны, то такой определитель равен нулю.
 .
.
Введем понятие минора и алгебраического дополнения определителя.
Выделим
в определителе 3гопорядка
элемент![]() и вычеркнемi-ую строку
иk-ый столбец. Оставшиеся
элементы образуют определитель второго
порядка, который и называютминоромMikэлемента
и вычеркнемi-ую строку
иk-ый столбец. Оставшиеся
элементы образуют определитель второго
порядка, который и называютминоромMikэлемента![]() .
.
Например
 .
.
Алгебраическое
дополнениеэлемента![]() определяется выражением
определяется выражением
![]() .
.
Схема
знаков
 для определителя 3гопорядка.
для определителя 3гопорядка.
Например
![]() .
.
7с)
Сумма произведений элементов
![]() некоторой строки (столбца) на алгебраические
дополнения этих элементов равна величине
определителя.
некоторой строки (столбца) на алгебраические
дополнения этих элементов равна величине
определителя.
![]() – это разложение по столбцуk.
– это разложение по столбцуk.
![]() – это разложение по строкеi.
– это разложение по строкеi.
Для определителя 3гопорядка:

Пример.
 .
.
Руководствуясь этим свойством, можно вычислить определитель любого порядка.
8с)
Сумма произведений элементов
![]() некоторой строки (столбца) на соответствующие
алгебраические дополнения элементов
другой строки (столбца) равна нулю, т.е.
некоторой строки (столбца) на соответствующие
алгебраические дополнения элементов
другой строки (столбца) равна нулю, т.е.
![]() .
.
Доказательство:
В данной сумме не участвуют элементы строки j. Значит она (эта сумма) от этих элементов не зависит. Поэтому данную строку можно заменить на любую другую, например наi-ю строку, но такой определитель равен нулю.
9с) Пусть определитель имеет следующий вид:
 ,
его можно записать в виде суммы 2хопределителей
,
его можно записать в виде суммы 2хопределителей
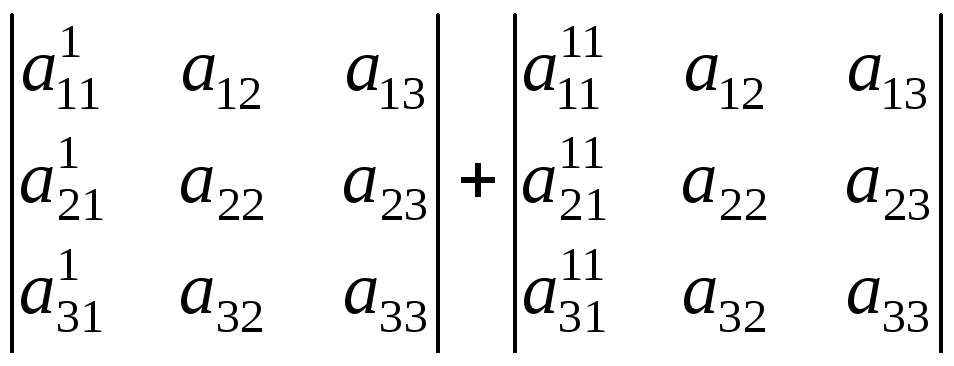 .
.
Доказать можно разложением по элементам первого столбца.
10с) Если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца) предварительно умноженные на одно и тоже число, то величина определителя не изменится.


![]() 0
0
 .
.
Применяя это свойство, удается упростить вычисление определителя.
Пример.

![]() .
.
Пользуясь этим свойством и разложением определителя по строке (столбцу) можно вычислять и определители более высоких порядков.
Пример.

![]() .
.
Решение системы линейных уравнений с помощью определителей
Рассмотрим систему трех линейных уравнений с тремя неизвестными.
(

 1)
1)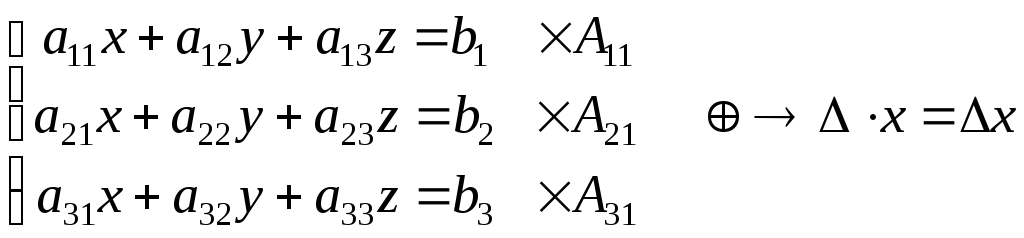


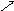




 .
.
![]() ;
;![]() ;
;![]() . (2)
. (2)
1)
![]() .
Получаем формулы Крамера.
.
Получаем формулы Крамера.
![]() ;
;![]() ;
;![]() .
(3)
.
(3)
Формулы (3) дают единственное решение системы. То, что это решение можно убедиться, подставив (3) в (1).
2)
![]() ,
но один из
,
но один из![]() .
.
Система не совместна, т.к. (2) не выполняются.
3)
![]() .
В этом случае система или не имеет
решений, или имеет их бесчисленное
множество. (Или несовместна, или
неопределенна).
.
В этом случае система или не имеет
решений, или имеет их бесчисленное
множество. (Или несовместна, или
неопределенна).
Рассмотрим выполнение заданий на вычисление определителей третьего порядка и решение систем трех линейных уравнений с тремя неизвестными.
Задание 1
Вычислить определитель
 .
.
Решение
Воспользуемся правилом треугольников : найдем сумму произведений элементов по левой схеме
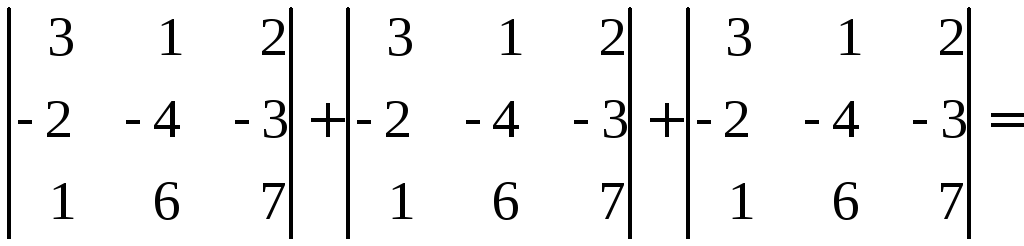







=3· (-4)·7 + 2·(-2) ·6 + 1·1·(-3) = -84 - 24 -3 = -111
и сумму произведений элементов по правой схеме






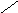

= 1·(-4)·2 + 1·(-2)·7 + 3·(-3)·6 = -8 - 14 -54 = -76.
Из первой суммы вычтем вторую и получим: Δ = -111 - (-76) = -111 + 76 = -35.
Ответ: Δ = -35.
Задание 2
Вычислить определитель
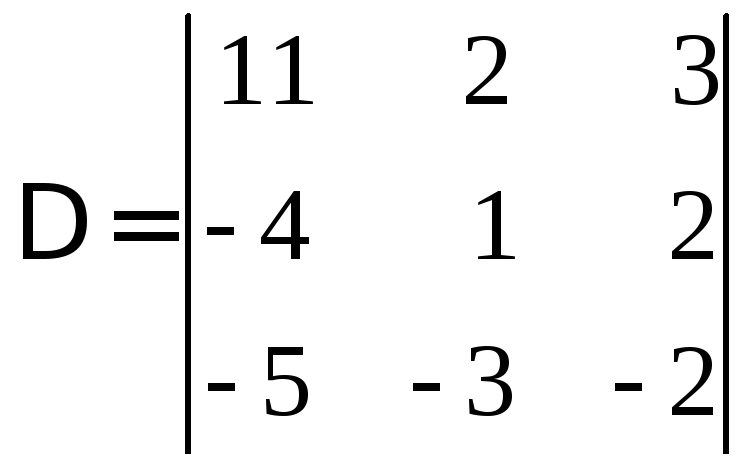 .
.
Решение
Воспользуемся правилом Саррюса . Припишем к данному определителю справа два его первых столбца:

 .
.
Вычислим сумму произведений элементов определителя, расположенных на главной диагонали и параллельно ей:

 =
= 11·1· (-2) + 2·2·(-5) +
3·(-4)·(-3) = -22 - 20 + 36 = -6.
=
= 11·1· (-2) + 2·2·(-5) +
3·(-4)·(-3) = -22 - 20 + 36 = -6.
и сумму произведений элементов, расположенных на побочной диагонали и параллельно ей:

 =
(-5)·1·3 +(-3)·2·11 + (-2)·(-4)·2 = -15 - 66 + 16 = - 65.
=
(-5)·1·3 +(-3)·2·11 + (-2)·(-4)·2 = -15 - 66 + 16 = - 65.
Из первой суммы вычтем вторую и получим: Δ = -6 - (-65) = -6 + 65 = 59.
Примечание. Для вычислений можно воспользоваться калькулятором. Последовательность действий может быть следующей:
11* 1* 2 М- 2*2*5 М- 3*4*3 М+ MRC -6
5*1*3 M- 3*2*11 M- 2*4*2 M+ MRC -65
- 6 + 65 = 59
или 11* 1* 2 М- 2*2*5 М- 3*4*3 М+ 5*1*3 M+ 3*2*11 M+ 2*4*2 M- MRC 59
Ответ: Δ = 59.
Задание 3
Вычислить определитель, разложив его по элементам первой строки
 .
.
Решение
Воспользуемся свойством 7 определителей:
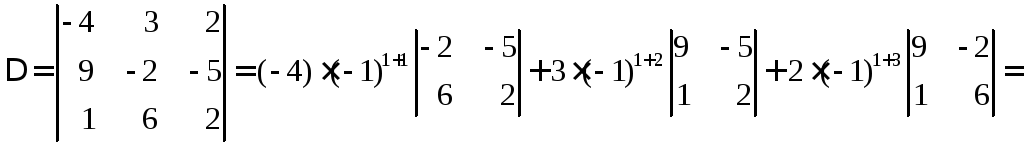
= (-4)((-2)·2 – (-5)·6) + 3·(-1)(9·2 – 1·(-5)) + 2·(9·6 - 1·(-2)) =
= (-4)(-4 + 30) – 3(18 + 5) + 2(54 + 2) = -104 – 69 + 112 = - 61.
Ответ: Δ = - 61.
Задание 4
Вычислить определитель
 .
.
Решение
Непосредственное вычисление данного определителя с помощью правила треугольников, правила Саррюса или разложение его по элементам какого-либо столбца (строки) привело бы к очень громоздким вычислениям. Поэтому целесообразно сначала преобразовать данный определитель, используя свойство 10. Величина определителя не изменится, если первую его строку сначала умножить на 2 и вычесть из второй, а затем умножить на 4 и вычесть из третьей:
 .
.
Полученный определитель (согласно свойству 7) можно разложить по элементам первого столбца, в котором только один элемент отличен от нуля:
 .
.
Ответ: Δ = 7422.
Задание 5
Не раскрывая определителя, доказать справедливость равенства
 .
.
Решение
Воспользуемся свойством 10 определителей. Величина определителя не изменится, если первый его столбец сначала умножить на 2 и прибавить ко второму, а затем умножить на 3 и прибавить к третьему:

Что и требовалось доказать.
Задание 6
Не раскрывая определителя, доказать справедливость равенства
 .
.
Решение
Воспользуемся свойством 10 определителей. Величина определителя не изменится, если первый его столбец прибавить к третьему:
 .
.
В полученном определителе соответствующие элементы второго и третьего столбцов пропорциональны, следовательно, в соответствии со свойством 6 определителей данный определитель равен нулю. Что и требовалось доказать.
Задание 7
Не раскрывая определителя, доказать справедливость равенства
 .
.
Решение
Воспользуемся свойством 9 определителей и представим исходный определитель в виде суммы двух определителей:
 .
.
Первый из этих определителей имеет два одинаковых столбца – первый и второй, а во втором соответствующие элементы первого и третьего столбцов пропорциональны, следовательно, в соответствии со свойством 6 определителей оба этих определителя равны нулю, а, следовательно, и данный определитель равен нулю. Что и требовалось доказать.
Задание 8
Решить
систему

Решение
Вычислим определитель системы:
 .
.
Так как Δ = -8 ≠ 0, то система имеет единственное решение, которое можно найти по формулам Крамера:
![]()
Для этого вычислим определители Δ1, Δ2 и Δ3:

Следовательно,
![]()
Ответ:
![]()
Задание 9
Решить
систему

Решение
Вычислим определитель системы
 .
.
Так как Δ = -23 ≠ 0, то система имеет единственное решение, которое можно найти по формулам Крамера:
![]()
Для этого вычислим определители Δ1, Δ2 и Δ3:

Следовательно,
![]()
Ответ:
![]()
Следующее задание выполните самостоятельно.
Задание 10
Решить
систему

Если у Вас получился ответ отличный от (0,5; 2; 1,5), то рассмотрите решение задания 10.
Решение задания 10.
Вычислим определитель системы:
 .
.
Так как Δ = 10 ≠ 0, то система имеет единственное решение, которое можно найти по формулам Крамера:
![]()
Для этого вычислим определители Δ1, Δ2 и Δ3:


 .
.
Следовательно,
![]() .
.
Ответ:![]()
