Задачи для самостоятельного решения

№	Задания	Ответы
1
2
3	2. Найти решения задач Коши
4
5
6
7
8

6.4. Однородные уравнения первого порядка

Уравнение вида (6.14) называется однородным уравнением первого порядка, если функция представляется в виде функции, зависящей только от величины:

=.

Таким образом, однородное уравнение первого порядка имеет вид

.

(6.27)

Для решения уравнения (6.26) используется подстановка , где- новая искомая функция. Производнаянаходится по формуле нахождения производной произведения, кроме этого. В результате подстановки последних выражений уравнение (6.27) преобразуется к виду

.

(6.28)

После переноса в правую часть уравнение (9.28) превращается в уравнение с разделяющимися переменными

.

(6.29)

Разделение переменных приводит уравнение (6.29) к виду

.

(6.30)

В результате интегрирования (6.30)

получаем

.

(9.31)

Здесь постоянная интегрирования представлена в виде для удобства записи окончательного ответа.

Дальнейший ход решения заключается в вычислении интеграла при известной функции.

Пример 6.7.

Найти общее решение уравнения .

Решение

,

, ,,

, ,,

, ,

, ,,

,

Ответ:

, где – произвольная постоянная.

6.5. Линейные дифференциальные уравнения первого по­рядка

Уравнение

.

(6.32)

где и – заданные функции, называется линейным дифференциальным уравнением пер­вого порядка.

Решение уравнения (6.32) будем искать в виде произведения

(6.33)

двух неизвестных функций и . Подстановка (6.33) в (6.32) дает . После преобразований получаем

.

(6.34)

Выражение в круглых скобках в уравнении (6.34) приравняем

нулю:

,

(6.35)

тогда из уравнения (6.34) и условия (6.35) следует равенство

.

(6.36)

Из уравнения (6.35), которое представляет собой уравнение с разделяющимися переменными, можно найти функцию . Далее найденную функциюподставим в уравнение (6.36) и будем решать его относительно второй неизвестной функции.

Разделяя переменные в уравнении (6.35) и интегрируя, последовательно получаем: ,,откуда

.

(6.37)

Подстановка функции из (6.37) в уравнение (6.36) дает

, откуда . Интегрируя последнее равенство, находим вторую неизвестную функцию

.

(6.38)

Возвращаясь к подстановке (6.33), находим общее решение уравнения (6.32) в виде

.

(6.39)

Полученное соотношение (6.39) можно рассматривать как формулу, дающую общее решение уравнения (6.32) при заданных функциях и.

Пример 6.8

Найти общее решение уравнения .

Решение

Это линейное дифференциальное уравнение первого порядка (6.32), в котором ,. Подставляя эти выражения дляив формулу (6.39) и вычисляя соответствующие интегралы, получаем

==

= .

Таким образом, – общее решение исходного уравнения.

Пример 6.9 (Закон перехода вещества в раствор.)

Рассмотрим процесс перехода вещества в раствор. Известно, что при фиксированной температуре количество вещества, содержащееся в определенном объеме растворителя, не может превзойти некоторого, определенного для каждого вещества числа , соответствующего насыщенному раствору. Известно также, что по мере приближения к насыщенному раствору уменьшается количество вещества, перехо­дящего в раствор за единицу времени. Иными словами, чем больше вещества перешло в раствор, тем меньше скорость перехода.

Решение

Пусть — количество вещества, перешедшего в раствор к моменту времени . Тогда — скорость перехода, и в соответствии со сказанным можно написать:

,

где стремится к нулю при, . Эксперименты по­казывают, что для многих веществ функция пропорциональна разности, т.е. , и, следовательно,

, где > 0 – коэффициент пропорциональности.

Далее преобразуем последнее уравнение к виду .

Это – линейное дифференциальное уравнение первого порядка.

Согласно формуле (6.39) имеем:

Пусть - момент времени, с которого начался процесс перехода ве­щества в раствор. Очевидно, . Поэтому , откуда , и, значит,

.

(6.40)

Значения и определяются характером растворенного вещества и растворителя. Из (6.40) видно, что при любых и величина стремится к , если . Вид функции хорошо согла­суется с экспериментальными данными. Поэтому формулу (6.40) можно рассматривать как закон перехода вещества в раствор.

Пример 6.10

Конденсатор емкостью включается в цепь с нап­ряжением и сопротивлением . Определить заряд конденсатора в момент после включения.

Решение. Сила электрического тока представляет производ­ную от количества электричества , прошедшего через проводник, по времени

В момент заряд конденсатора и сила тока ; в цепи дейст­вует электродвижущая сила Е, равная разности между напряже­нием цепи и напряжением конденсатора , т. е.

Согласно закону Ома

Поэтому

Отсюда:

Теперь согласно формуле (6.39) имеем:

.

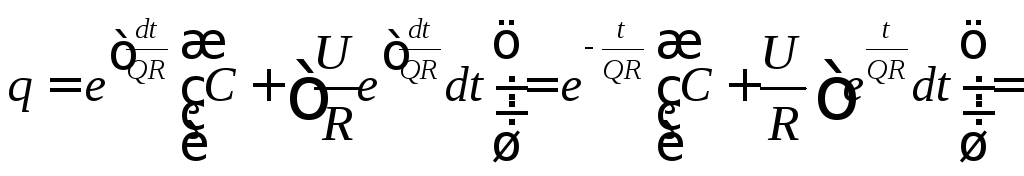
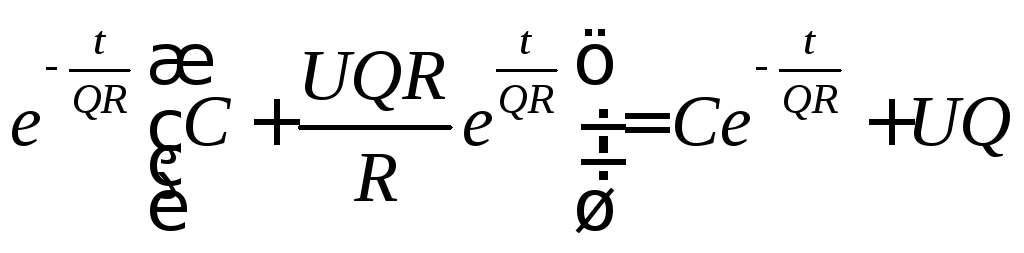По условию при и потому и.

Таким образом, в момент времени

.
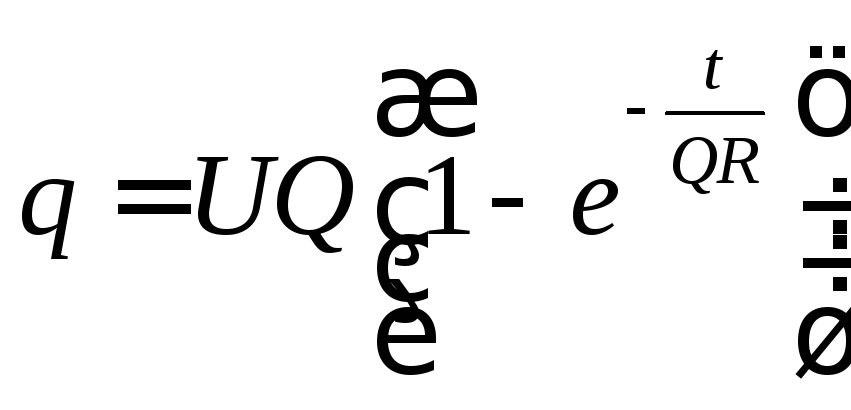