3. Амплитудная манипуляция.

Если передаваемое сообщение представляет собой последовательность прямоугольных импульсов (рис. 5.3, а), т.е. является дискретным сообщением, то при образовании модулированного сигнала амплитуда переносчика (несущей) принимает всего два значения, т.е. осуществляется амплитудная манипуляция. Иногда манипуляцию называют дискретной модуляцией.

В зависимости от значения коэффициента m различают два варианта амплитудной манипуляции: 1) при m < 1 (рис. 5.3, б, на котором показана идеализированная форма импульсов) и 2) при m=1 (рис. 5.3, в), на котором показана форма реальных импульсов на выходе фильтра.

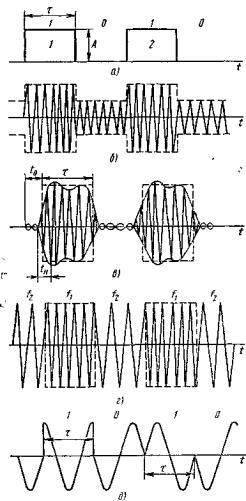
Рис. 5.3. Виды манипуляций:

а – передаваемое сообщение, б – амплитудная манипуляция при m=0,5, в – амплитудная манипуляция при m=1, г – частотная манипуляция, д – фазовая манипуляция

Амплитудную манипуляцию широко применяют как в телемеханике, так и в связи. Спектр частот при амплитудной манипуляции, как и при амплитудной модуляции, содержит кроме несущей верхнюю и нижнюю боковые полосы частот. Составляющие верхней боковой полосы содержат частоты F_ω0 + k/, а составляющие нижней боковой – частоты F_ω0 – k/, где k=1, 2, ... (рис. 5.4, а, б).

Амплитуда составляющих зависит от коэффициента модуляции т. Так же как и при немодулированной последовательности, число гармоник в каждом лепестке спектра увеличивается с увеличением скважности, а их амплитуда падает.

Амплитуда несущей частоты вписывается в огибающую спектра при 100%-ной манипуляции (m=1) (рис. 5.4, б). При уменьшенном коэффициенте т энергия несущей возрастает, а энергия боковых частот падает.

На рис. 5.3, в, показана форма радиоимпульсов при амплитудной манипуляции на выходе полосового фильтра. t₀ – групповое время запаздывания, а t_н – время нарастания. И в этом случае необходимая ширина полосы частот определяется допустимой степенью искажения формы импульсов при передаче. Эта форма импульсов существенно зависит от времени нарастания t_н.

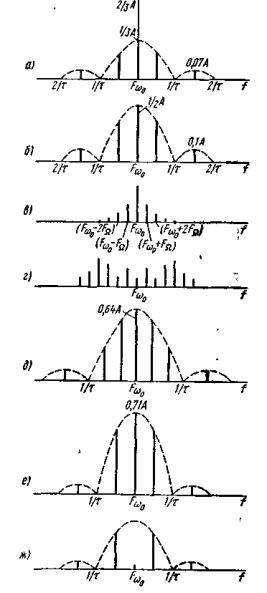
Рис. 5.4. Спектры частот:

а – при амплитудной манипуляции m=0,5, б – при амплитудной манипуляции с m =1, в – при частотной модуляции с m=1; г – при частотной модуляции с m=5, д – при частотной манипуляции с m=1; е – при фазовой манипуляции, =±90°; ж – при фазовой манипуляции, =±180°

Вопросы оценки полосы частот амплитудной манипуляции рассмотрены в разделе 5.6 «Спектры импульсных сигналов».

5.3. Частотная модуляция

Частотная модуляции (ЧМ) – это изменение частоты переносчика (несущей) пропорционально мгновенному значению сообщения. На рис. 5.1, д показано, что при увеличении мгновенных значений сообщения частота несущей увеличивается, а при отрицательной полуволне сообщения – уменьшается, при этом амплитуда модулированного сигнала остаётся постоянной. Если ω – угловая частота модулированного колебания (сигнала), ω₀ – среднее значение угловой частоты переносчика и  – угловая частота сообщения, то можно записать

ω=ω₀ + m_чcost, (5.9)

где

m_ч =ω/ (5.10)

– коэффициент частотного отклонения, или глубина частотной модуляции; ω – девиация угловой частоты, или максимальное отклонение частоты переносчика (в одну сторону) от исходного значения.

Девиация частоты зависит от амплитуды модулирующего сообщения (см. рис. 5.1, д). При увеличении амплитуды сообщения частота переносчика F_ω0 возрастает, при уменьшении (отрицательная полуволна сообщения на рис. 5.1, а) – снижается. Девиация частоты и индекс модуляции связаны соотношением F_дев= т_чF_.

Пример 5.1

Если F_ω0 = 10 000 Гц, F_ = 500 Гц и m_ч=3, то максимальная девиация частоты F_дев = т_чF_ = 3·500 = 1500 Гц, т.е. переносчик в процессе модуляции может изменить свою частоту до 11 500 или 8500 Гц.

Полагая, что начальная фаза равна нулю (при t =0), можно записать уравнение сигнала при частотной модуляции:

u_ЧМ =U_ω0cos(ω ₀t + m_ч sint). (5.11)

На рис. 5.7, в-д представлен спектр при частотной модуляции. Строго говоря, спектр частот при ЧМ бесконечно велик, и для точного воспроизведения передаваемого сообщения нужна бесконечно большая ширина полосы. Однако боковые частоты высших порядков имеют ничтожную интенсивность и ими можно пренебречь. Полоса частот при ЧМ может быть приближенно определена из выражения

F_ЧМ =2F_min(m_ч+ 1)=2(F_{ max} + F_дев). (5.12)

В телеизмерении оптимальное значение т_ч зависит от требуемой точности передачи. Так, для систем ТИ с погрешностью δ = 1% оптимальный индекс частотной модуляции т_ч.опт=5. Для точных систем ТИ (δ=0,1 %) т_ч.опт=15.