tv_ms_1

Решение. Плотность распределения не имеет максимума, а следовательно мода не существует. Однако легко заметить, что кривая распределения симметрична относительно прямой х=0, следовательно .

#289

Случайная величина Х при х≥0 задана плотностью вероятности (распределение Вейбулла) ; . Найти моду Х.

Решение.

#290

Доказать, что математическое ожидание непрерывной случайной величины заключено между наименьшим и наибольшим её возможными значениями.

Решение. Пусть Х – непрерывная случайная величина, заданная плотностью распределения f(x) на отрезке [a, b]; вне этого отрезка f(x)=0. Тогда a≤x≤b. Учитывая, что f(x)=0, получим . Проинтегрируем это двойное неравенство в пределах от a до b:

.

Принимая во внимание, что

,

Окончательно получим .

#291

Доказать, что если и , то

.

Решение.

#292

Случайная величина Х в интервале (-c, c) задана плотностью распределения , вне этого интервала f(x)=0. Найти дисперсию Х.

Решение. Будем искать дисперсию по формуле

.

Подставляя М(Х)=0, получим

.

Сделав подстановку x=csint, окончательно имеем D(X)=c² /2.

#293

Условие задачи:

Случайная величина Х в интервале (-3,3) задана плотностью распределения

f(x) = 1/(π); вне этого интервала f(x) = 0. а) Найти дисперсию Х; б) Что вероятнее: в результате испытания окажется Х > 1 или Х < 1?

Решение задачи:

а) Будем искать дисперсию по формуле:

D(x) = ,

где М(x) – математическое ожидание величины Х, вычисляемое по формуле:

М(x) =

Подставим a = -3, b = 3, f(x) = 1/(π), получим:

M(x) =

Учитывая, что подынтегральная функция нечетная и пределы интегрирования симметричны относительно начала координат, заключаем, что интеграл равен нулю, т.е. M(x) = 0. Подставляя это значение в формулу для вычисления дисперсии, получим:

D(x) =

Сделаем замену x = 3sin t, dx = 3cos t dt, тогда окончательно имеем D(x) = 9/2.

б) Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), определяется равенством:

P (a < x < b) =

Тогда P (-3 < x < 1) = 0,5 + (1/π)arcsin(1/3)

P (1 < x < 3) = 0,5 - (1/π)arcsin(1/3)

Получаем, что вероятнее в результате испытания окажется x < 1.

#294

Условие задачи:

Доказать, что дисперсию непрерывной случайной величины X можно вычислить по формуле:

D(X) =

Указание: Воспользоваться формулой

D(X) = (1)

и равенствами . (2)

Решение задачи:

Дисперсия непрерывной случайной величины Х ищется по формуле:

D(X) =

Преобразуем эту формулу следующим образом:

D(X) = =

Воспользовавшись равенствами (2), получим:

D(X) =

Ч.т.д.

#295

Условия задачи:

Случайная величина X в интервале (0, π) задана плотностью распределения

f(x) = .

Вне этого интервала f(x) = 0. Найти дисперсию X.

Решение задачи:

Найдем дисперсию по формуле:

D(X) =

Подставив сюда M(Х) = π/2 (кривая распределения симметрична относительно прямой x = π/2), а = 0, b = π , f(x) = , получим:

D(X) =

Дважды интегрируя по частям, найдем

Тогда получим

#296

Условие задачи:

Случайная величина X в интервале (0, 5) задана плотностью распределения

;

вне этого интервала f(x) = 0. Найти дисперсию X.

Решение задачи:

Найдем дисперсию по формуле:

D(X) =

где М(x) – математическое ожидание величины Х, вычисляемое по формуле:

М(X) =

Взяв a = 0, b = 5, , получим

Тогда D(X) =

#297

Условие задачи:

Найти дисперсию случайной величины Х, заданной функцией распределения

0 при x ≤ -2

F(x) = при -2 < x ≤ 2

1. при x > 2.

Решение задачи:

Найдем плотность распределения

0 при x ≤ -2

f(x) = F’(x) = ¼ при -2 < x ≤ 2

0. при x > 2

Найдем математическое ожидание по формуле

М(X) =

M(X) = ,

т.к. подынтегральная функция нечетная, и пределы симметричны относительно начала координат.

Найдем искомую дисперсию по формуле:

D(X) =

D(X) =

#298

Условие задачи:

Случайная величина задана функцией распределения

F(x) = при x ≥ (> 0),

0. при x < .

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение X.

Указание: Найти сначала плотность распределения, использовать формулу:

D(X) =

Решение задачи:

Найдем плотность распределения:

при x ≥ (> 0),

f(x) = F’(x) = 0 при x < .

Найдем математическое ожидание по формуле

М(X) =

M(X) =

Найдем дисперсию по формуле:

D(X) =

D(X) =

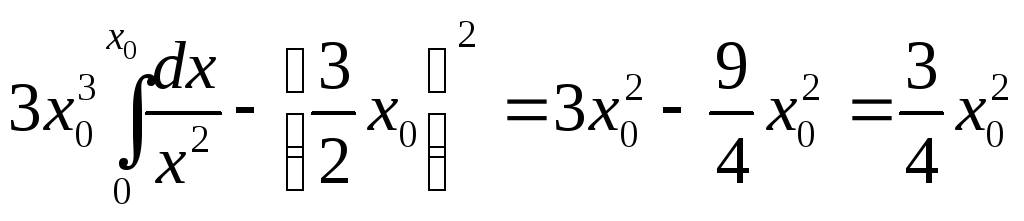
Среднее квадратическое отклонение случайной величины X находится по формуле:

#299

Условие задачи:

Случайная величина X в интервале (0, π) задана плотностью распределения ; вне этого интервала . Найти дисперсию функции , не находя предварительно плотности распределения Y.

Решение задачи:

Для вычисления дисперсии используем формулу:

D[φ(x)] =

Подставив , , a = 0, b = π, получим

= M[] =

Тогда

Интегрируя по частям, найдем .

Тогда .

#300

Условия задачи:

Случайная величина X задана плотностью распределения в интервале (0, π/2); вне этого интервала . Найти дисперсию функции , не находя предварительно плотности распределения Y.

Указание: Использовать формулу:

D[φ(x)] =

и то, что M() = (см. задачу 283).

Решение задачи:

Для вычисления дисперсии используем формулу:

D[φ(x)] =

Подставив , , a = 0, b = π/2, имея M() = , получим

Интегрируя по частям, найдем .

Тогда