Метод_лаб_2011_ТПР_стац_pdf

11

Ожидаемая полезность события – сумма произведений вероятностей возникновения данного события на значение полезности последствий этих

Выбор ЛПР в условиях риска формализуется при помощи понятия потери, при этом ЛПР проявляет свои индивидуальные вкусы и склонность к риску. Решение ЛПР может быть найдено на основе следующего алгоритма:

1 Присваиваются произвольные значения полезности выигрышу для лучшего и худшего последствия, причем худшему из последствий ставится в соответствие меньшее значение полезности.

2 Игроку предоставляется выбор:

- получить определенную гарантированную сумму W, которая находится в промежутке между худшим (s) и лучшим (S) значениями выигрышей s W S ;

- принять участие в игре, т.е. получить с вероятностью р наибольшую денежную сумму S и с вероятностью (1-р) получить наименьшую денежную сумму s, при этом вероятность следует изменять (уменьшать или повышать) до тех пор пока ЛПР не станет безразличным к отношению выбора между гарантированной суммой и игрой.

Безусловный денежный эквивалент (БДЭ) – максимальная сумма денег,

которую ЛПР готов заплатить за участие в игре (лотерее) или минимальная сумма денег, за которую он готов отказаться от игры.

Ожидаемая денежная оценка (ОДО) – средний выигрыш в игре.

8 Функция с интервальной нейтральностью к риску.

Одним из основных видов функции полезности, характеризующей финансовое поведение людей, является функция U(x) lnx , т.е. полезность

12

бесконечно малого выигрыша прямо пропорциональна этому выигрышу и обратно пропорциональна денежной сумме, которой игрок обладает. Из этого следует, что если полезность описывается функцией U(x) lnx , то потери более ощутимы, чем выигрыш.

Детерминированный эквивалент лотереи L – это гарантированная сума

Премия за риск – это сумма, которой субъект готов пожертвовать из среднего выигрыша за то, чтобы избежать риска, связанного с лотерей. Премию за риск определяют таким образом:

Страховая сумма – величина детерминированного эквивалента с противоположным знаком.

13

ЛАБОРАТОРНАЯ РАБОТА № 3 Принятие оптимального решения на основе теории игры

Цель: научиться осуществлять выбор альтернативы на основе теории игры и применять полученные знания при создании программных продуктов.

бракованной продукции. Определяют состояния внешней среды: 1 – пригодная партия изделий, 2 – бракованная партия изделий.

Пусть бракованные изделия в пригодной партии составляют %б( 1 ), в непригодной – %б( 2 ). Проведенные на предприятии расчеты показывают, что вероятность производства бракованной партии составляет p( 2 ) .

Предприятие отправляет партии товаров m потребителям, для которых контрактом обусловленный возможный предельный процент бракованных деталей – %б-потреб-l соответственно. За один процент превышения установленных границ предполагается штраф размером P тыс.грн. С другой стороны, производство партии товаров более высокого качества увеличивает затраты предприятия на V тыс.грн. за каждый процент.

В результате проверки двух изделий из всей партии может быть установлено, что: 1) оба изделия пригодны; 2) одно из изделий пригодно; 3) оба изделия бракованы. Пусть 1 , 2 , 3 – эти три возможные события соответственно.

Задание. Построить программный модуль, позволяющий:

1)принять оптимальное решение в условиях отсутствия риска (гарантированный результат);

2)принять оптимальное решение, используя априорные вероятности

событий;

3)принять оптимальное решение, используя апостериорные вероятности

событий.

Исходные данные представлены в таблице 1. Процент брака выбирается студентом случайным образом в заданных границах, используя генератор случайных чисел.

Предусмотреть возможность ввода задаваемого пользователем количества альтернатив (покупателей), величин процента бракованной продукции и вероятностей пребывания внешней среды в одном из своих состояний.

Программа должна выдавать сообщение о выборе оптимальной альтернативы в каждом конкретном случае (при использовании различной информации и при указанных результатах контрольной проверки деталей), а также критерий, с помощью которого принималось решение.

14

Таблица 1 – Исходные данные

Краткие теоретические сведения

Статистическая игра – это основная модель теории принятия решений в условиях частичной неопределенности.

Статистическая игра – игра с природой, модель ситуации принятия решений в условиях неопределенности и риска.

Природа – совокупность внешних обстоятельств, в которых приходится принимать решения или совокупность неопределенных факторов влияющих на эффективность принимаемых решений.

Человек – лицо, принимающее решение (ЛПР), или статистик.

Задача ЛПР – принятие наилучшего управленческого решения в каждой конкретной ситуации с учетом имеющейся информации.

Под стратегией природы понимают полную совокупность внешних условий, в которых приходится принимать решение. Данную совокупность назовем состоянием природы (П). В общем случае существует некоторое множество возможных состояний природы: ={ 1, 2,…, j,…, n}, которое называется пространством состояния природы, а элементы j – чистыми стратегиями природы.

15

Обычно известен только перечень чистых стратегий природы (нет полного знания о состоянии природы), и из прошлого опыта известно, как часто природа применяет ту или иную из своих чистых стратегий, т.е. известно априорное

вероятностей различных состояний природы. Оптимальной считается стратегия

Применяя этот критерий, отступают от условий полной неопределенности (отсутствия информации о состоянии природы), считая, что возможным состояниям природы можно приписать определенную вероятность их появления. В этом случае, определив математическое ожидание выигрыша для каждого решения, выбирают то, которое обеспечивает наибольшее значение выигрыша.

Принцип Байеса–Лапласа можно применять, если состояния природы, которые изучаются, и решения, которые принимаются, многократно повторяются. Тогда, например, статистическими методами, базируясь на частотах появления отдельных состояний природы в прошлом, можно оценивать вероятности их появления в будущем.

Перечисленные критерии не исчерпывают всего многообразия критериев выбора решения в условиях неопределенности, в частности, критериев выбора наилучших смешанных стратегий.

Оптимальное поведение по большей части зависит от принятого критерия оптимизации. Поэтому выбор критерия является вопросом ответственности в исследовании операций. Каждый выбор критерия предопределяет одобрение решения, которое может отличаться от решения, принятого в соответствии с другим критерием. Однако ситуация никогда не бывает настолько неопределенной, чтобы нельзя было получить хотя бы частичную информацию о вероятностях распределения состояний природы в ситуации, которая анализируется. В этом случае, оценив распределение вероятностей состояний природы, применяют критерий Байеса–Лапласа или проводят эксперимент, который дает возможность уточнить поведение природы.

Суть этого критерия заключается в выборе такого решения, чтобы не допустить излишне больших потерь, к которым может привести принятие ошибочного решения. Для этого строится «матрица рисков», элементы которой показывают, какой убыток понесем, если для каждого состояния природы не выберем наилучшего решения.

Риском игрока при выборе некоторого решения (стратегии) А называется разница между максимальным выигрышем, который можно получить в этих условиях, и выигрышем, который получит игрок в тех же условиях, применяя стратегию Аi. Обозначим эту величину через rij. Если бы игрок знал заранее будущее состояние природы Пj, то выбрал бы стратегию, которая отвечала максимальному элементу в указанном столбце: mахаij. Тогда, по определению,

риск равняется Rij = maxaij–aij. Матрица рисков строится так:

1)определяется для каждого состояния природы (столбика) наибольший

элемент;

2)элемент матрицы рисков получается вычитанием соответствующего элемента платежной матрицы из максимального элемента этого столбика.

Критерий Севиджа рекомендует в условиях неопределенности выбирать решение, которое обеспечивает минимальное значение максимального риска.

Критерии Вальда и Севиджа ориентируют статистика на самые неблагоприятные состояния природы, т.е. выражают пессимистическую оценку ситуации.

5 Критерий Гурвица (критерий пессимизма–оптимизма). Оптимальной

Пример

Предприятие выпускает определенную продукцию партиями фиксированного размера. Из-за случайных сбоев в производственном процессе возможен выпуск партий с недопустимо высоким процентом бракованной продукции. Определяют состояния экономической среды: 1 – пригодная партия изделий 2 – бракованная партия изделий. Пусть бракованные изделия в пригодной партии составляют 4%( 1 ), в непригодной – 15%( 2 ). Проведенные на

19

Ситуация 2. Результат эксперимента показал, что одно изделие качественное:

Минимум ожидаемых затрат достигается при реализации второй стратегии – отправить продукцию необходимо второму покупателю.

20

Лабораторная работа №4 Принятие многоцелевых решений

Цель: научиться осуществлять выбор альтернативы в условиях наличия множества целей, критериев и нескольких информационных ситуаций, применять полученные знания при создании программных продуктов.

позволяет получить ситуацию принятия решений с одним скалярным функционалом оценивания для заданной информационной ситуации I и критерия принятия решений.

Определить в соответствии с исходными данными (таблица 1) оптимальное решение. Функционалы оценивания строятся таким образом, чтобы не было идентичного повторения матриц, используя генератор случайных чисел в пределах заданного диапазона.

Использовать при определенном типе информационной ситуации:

2)I 4 – критерий Лапласа;

3)I 5 – критерий Вальда;

4)I 6 – критерий Гурвица ( 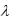0.6 ).

Приоритет задается студентом самостоятельно с помощью соответствующих весовых коэффициентов.

Построить программный модуль для принятия многоцелевых решений, предусмотреть возможность ввода исходных данных пользователем, информативность алгоритма, вывод по результатам оценки альтернатив по критерию.