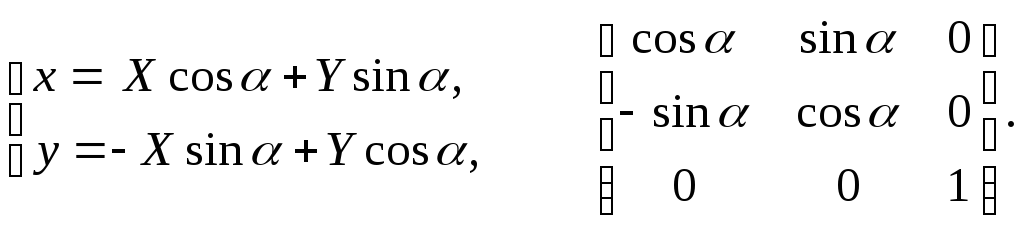Краткие теоретические сведения Аффинные преобразования на плоскости
Зададим некоторую
двумерную систему координат
.
Аффинное преобразование координат
описывается формулами
где
— константы. Значения
можно трактовать как координаты в
новой системе координат.
Обратное
преобразование
в
также является аффинным:
Аффинное
преобразование удобно записывать в
матричном виде. Константы
образовывают матрицу преобразования,
которая, будучи умноженная на
матрицу-столбец координат
,
дает матрицу-столбец
.
Однако для того, чтобы учесть константы
и
,
необходимо перейти к так называемымоднородным
координатам
— добавим строку с единицами в матрицах
координат:
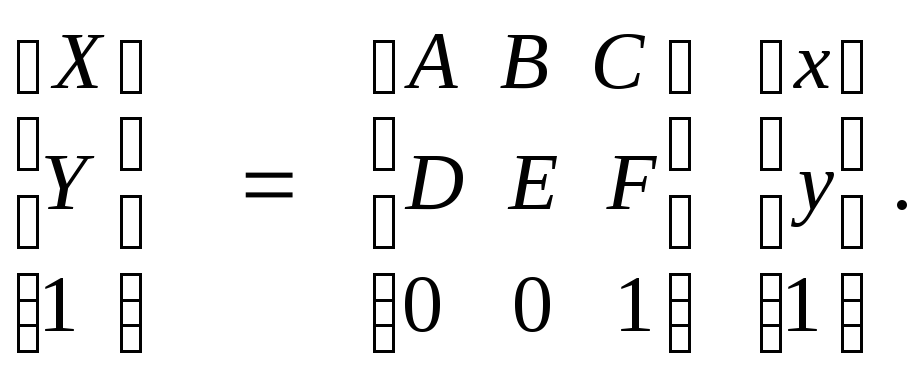
Матричная запись дает возможность наглядно описывать несколько преобразований, которые идут одно за другим. Например, если необходимо сначала выполнить преобразования
а потом — другое преобразование
то это можно описать как
Однако вместо двух преобразований можно выполнить только одно
где матрица
равна
произведению
.
Перемножение матриц выполняется так, как это принято в линейной алгебре. Рассмотрим частные случаи аффинного преобразования.
Параллельный сдвиг координат (рис. 2.1).
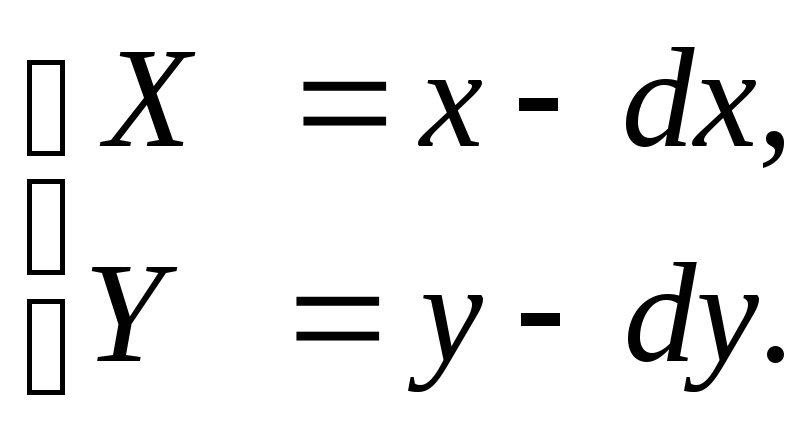
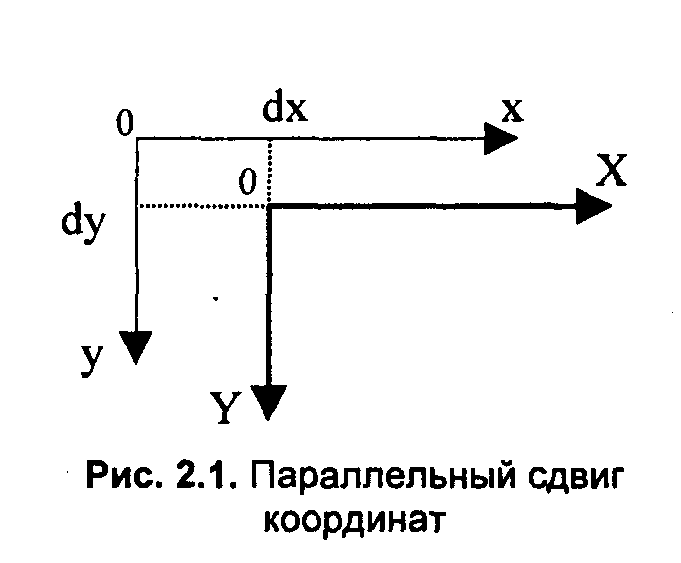
В матричной форме:
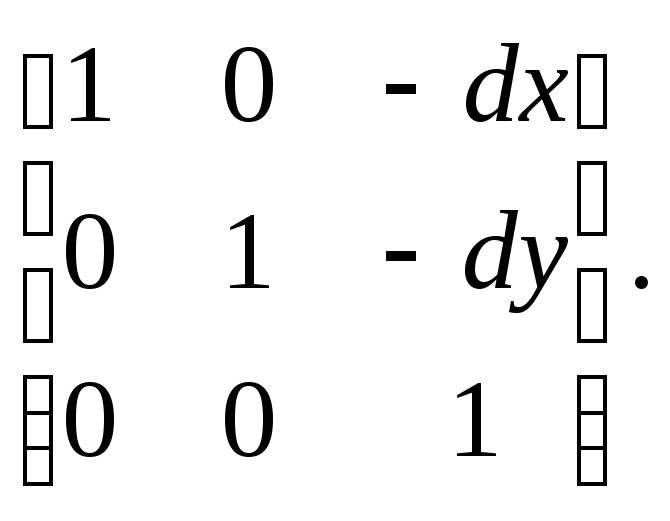
Рис. 2.1 Параллельный сдвиг
координат
Обратное преобразование:
Растяжение-сжатие осей координат (рис. 2.2).
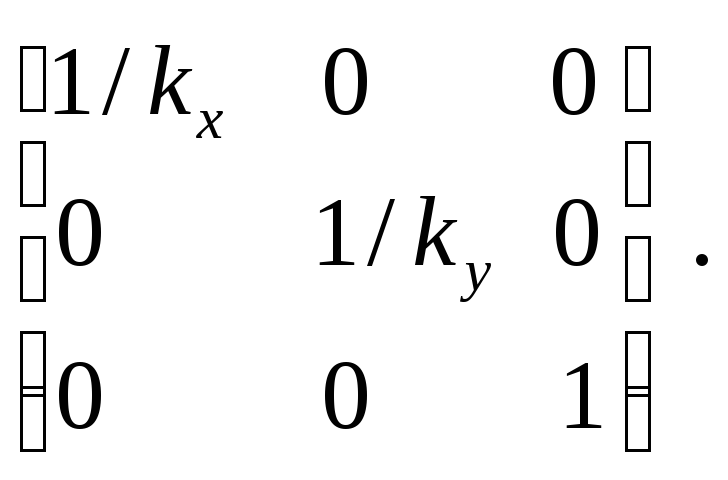Рис.
2.2.
Растяжение/сжатие
осей координат
Обратное преобразование:
Коэффициенты
и
могут быть отрицательными. Например,
соответствует зеркальному отражению
относительно осиу.
Поворот (рис. 2.3).
Рис. 2.3. Поворот
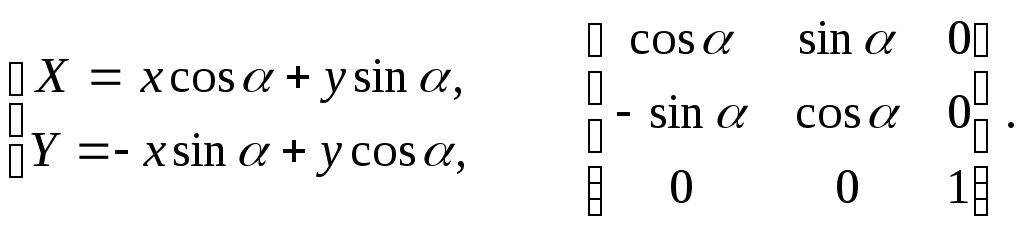
Обратное
преобразование соответствует повороту
системы
на угол (
).
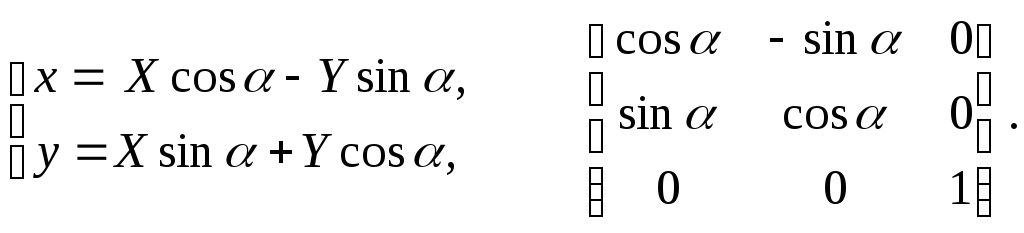
Свойства аффинного преобразования.
Любое аффинное преобразование может быть представлено как последовательность операций из числа указанных простейших: сдвиг, растяжение/сжатие и поворот.
Сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.
Аффинные преобразования объектов на плоскости
Аффинные преобразования объектов на плоскости описываются так:
где
— константы;
— координаты
до преобразования;
—
новые координаты точек объектов.
Рассмотрим частные случаи аффинного преобразования.
Сдвиг (рис. 2.7).
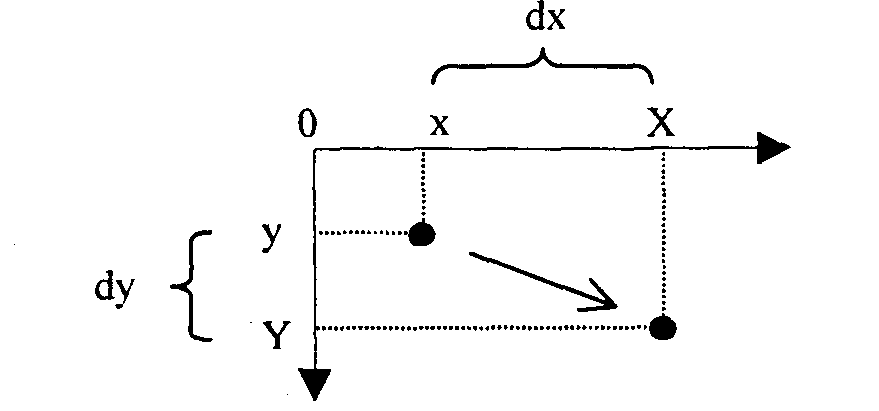
Рис. 2.7. Сдвиг
В матричной форме:
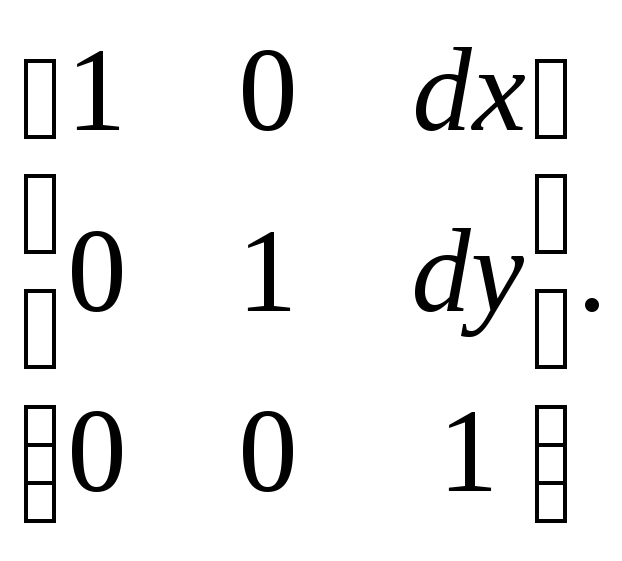
Обратное преобразование позволяет рассчитать старые координаты точек объектов по известным новым координатам:
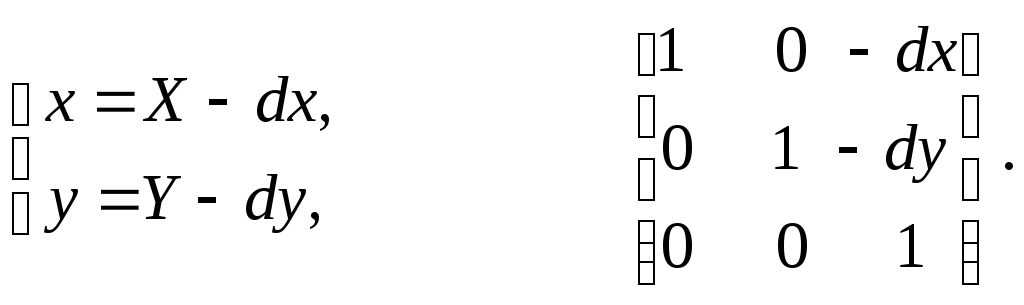
Растяжение-сжатие (рис. 2.8).
Необходимо отметить, что это, вероятно, не очень удачное название, так как для некоторых типов объектов размеры и форма не изменяются — например, для точечных объектов. По-другому это преобразование можно назвать масштабированием.
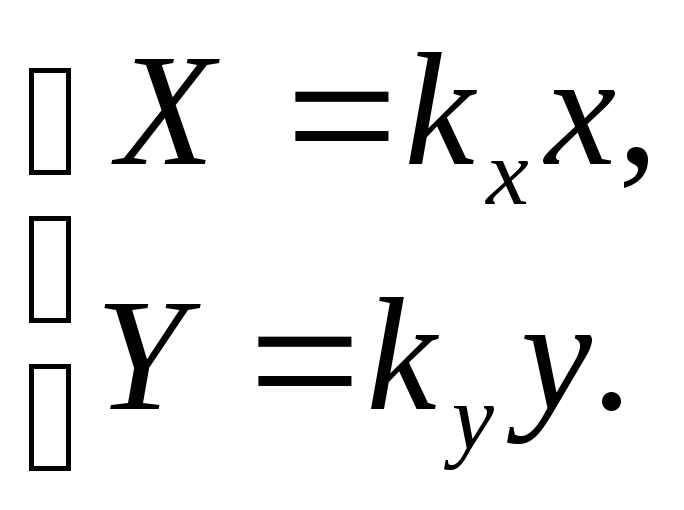
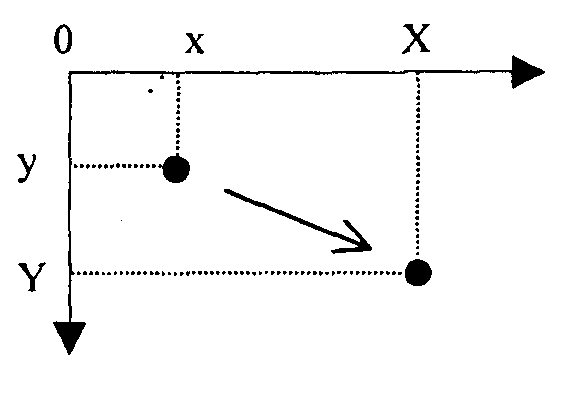
Рис. 2.8. Растяжение/сжатие
В матричной форме:
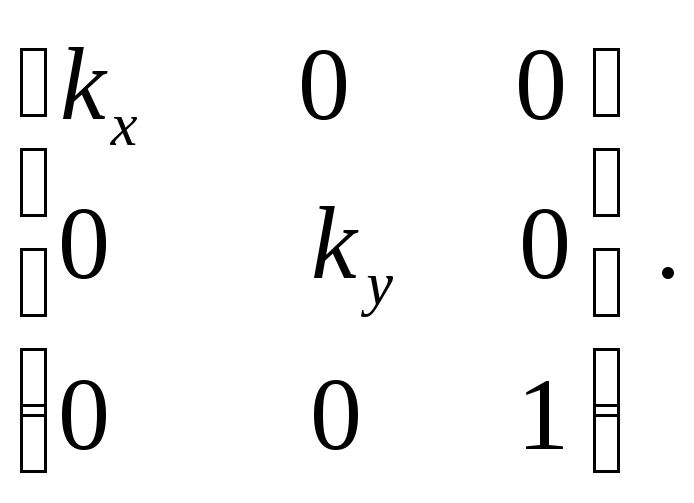
Обратное преобразование:
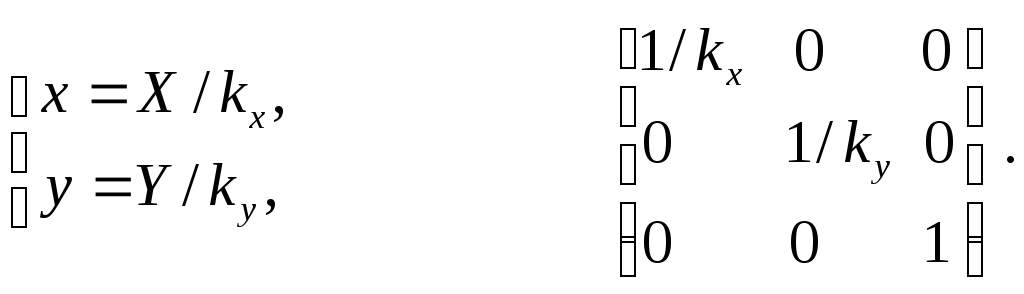
Поворот вокруг центра координат (0, 0) (рис. 2.9).
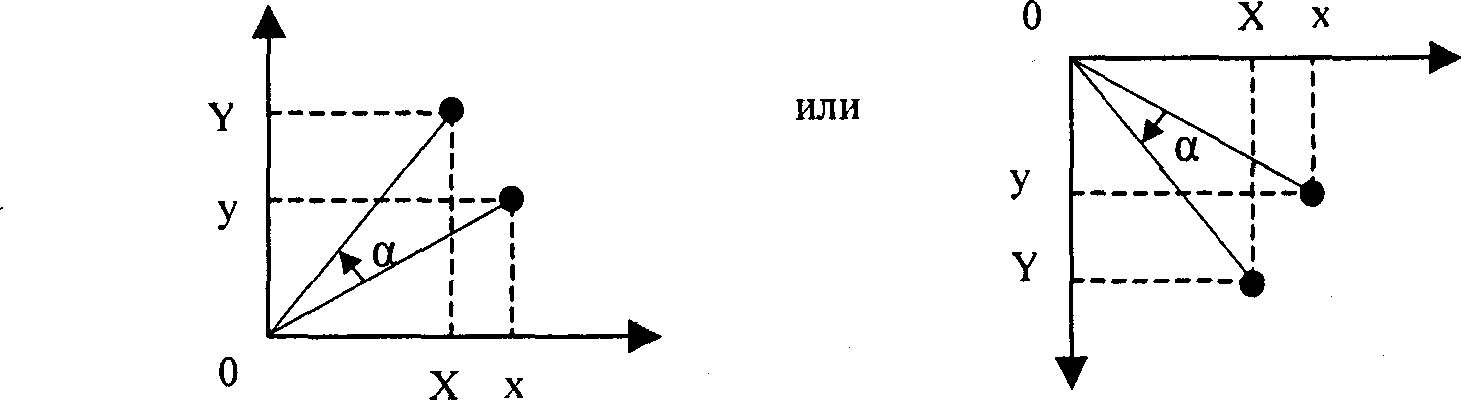
Рис. 2.9. Поворот объекта
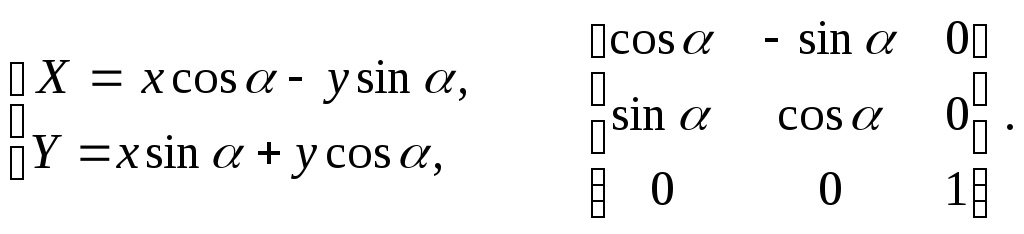
Формулы для
обратного преобразования можно получить,
если представить себе поворот точки
с координатами
на угол
(-
):
