
- •Тема: Аналитическая геометрия на плоскости и в пространстве Лекция № 7 “Прямая на плоскости. Основные задачи”
- •1. Общее уравнение прямой.
- •2. Виды уравнений прямой.
- •3. Основные задачи.
- •Лекция № 8 “Кривые второго порядка”
- •1. Окружность.
- •2. Эллипс.
- •3. Гипербола.
- •4. Парабола.
- •Лекция № 10 “Плоскость в пространстве”
- •1. Общее уравнение плоскости.
- •2. Другие уравнения плоскости.
- •3. Основные задачи.
- •Лекция № 11 “Прямая в пространстве”
- •1. Общее уравнение прямой.
- •2. Основные задачи.
Лекция № 11 “Прямая в пространстве”
1. Общее уравнение прямой.
Прямая в пространстве может быть задана как пересечение двух плоскостей:
 .
(1)
.
(1)
О1. Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
З1. Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей,
определяющих
прямую,
![]() и
и![]() были неколлинеарными, т.е. выполняется
одно из неравенств:
были неколлинеарными, т.е. выполняется
одно из неравенств:![]() или
или![]() .
.
Пусть прямая
проходит через точку
![]() параллельно вектору
параллельно вектору
![]() ,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:
,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:
![]() .
(2)
.
(2)
З2. Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример 1.
Как расположена прямая
![]() относительно координатных осей.
относительно координатных осей.
Согласно замечанию
2 эта прямая будет перпендикулярна осям
абсцисс и ординат (параллельна оси
аппликат) и будет проходить через точку
![]() .
.
Приравняв каждую
дробь уравнения (2) параметру
![]() ,
получимпараметрическое
уравнение прямой:
,
получимпараметрическое
уравнение прямой:

Пример 2.
Записать уравнение прямой
![]() в параметрическом виде.
в параметрическом виде.
Приравняем каждую
дробь к параметру
![]() :
: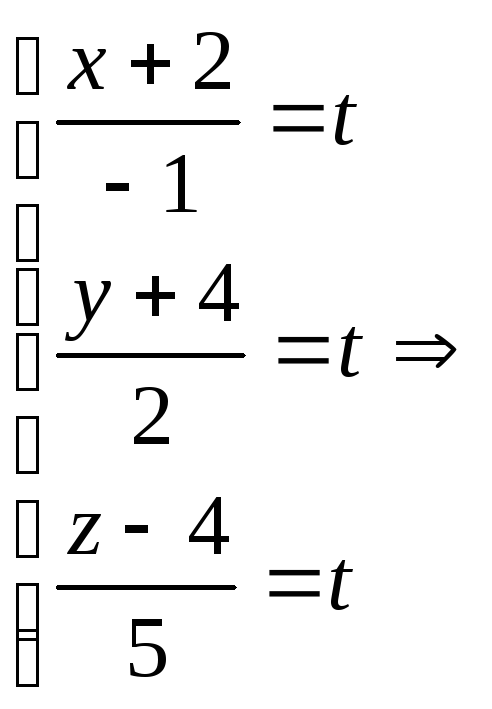
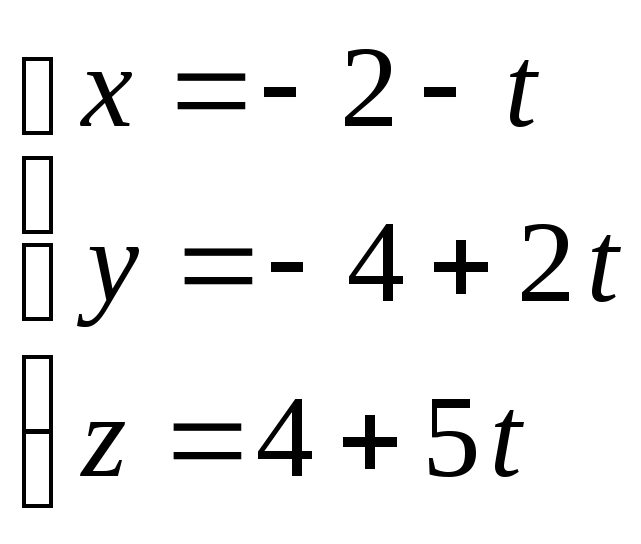 .
Если пря-
.
Если пря-
мая проходит через
две известные точки
![]() и
и![]() ,
то ее уравнение имеет вид (см.Лекцию
№ 7):
,
то ее уравнение имеет вид (см.Лекцию
№ 7):
![]()
![]() и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.
и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.
2. Основные задачи.
а) Переход
от общего уравнения прямой к каноническому.
Пусть прямая задана общим уравнением
 .
Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:
.
Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:
– находят
координаты любой точки, удовлетворяющие
приведенной системе, для чего одну из
переменных величин, например
![]() ,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;
,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;
– направляющий
вектор
![]() прямой находят как векторное произведение
нормальных векторов
прямой находят как векторное произведение
нормальных векторов
![]() и
и
![]() :
:
![]() ;
;
– зная точку, через которую проходит прямая, и направляющий вектор прямой записывают каноническое уравнение прямой.
Пример 3.
Записать уравнение прямой
 в каноническом и параметрическом виде.
в каноническом и параметрическом виде.
Положив
![]() ,
получим СЛАУ
,
получим СЛАУ Складывая уравнения, найдем
Складывая уравнения, найдем![]() .
Подставив это значение переменной
.
Подставив это значение переменной![]() во второе уравнение системы, по-лучим
во второе уравнение системы, по-лучим![]() .
Таким образом, прямая проходит через
точку
.
Таким образом, прямая проходит через
точку
![]() .
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:
.
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:
б)
Угол
между пересекающимися прямыми.
Угол
между двумя пересека-ющимися прямыми
определяется как угол между их
направляющими векторами.
Если прямые
![]() и
и![]() имеют направляющие вектора
имеют направляющие вектора
![]() и
и
![]() ,
,
соответственно, то угол между прямыми определяется по формуле:
![]() .
.
Сл1.
Если
прямые перпендикулярны (![]()
![]() ),
тоусловием
перпен-дикулярности
прямых является
равенство:
),
тоусловием
перпен-дикулярности
прямых является
равенство:
![]() .
.
Сл2.
Если прямые параллельны, то направляющие
вектора коллинеарны, следовательно,
условие
параллельности прямых:
![]() .
.
в)
Координаты
точки пересечения прямой и плоскости.
Пусть прямая
![]() задана общим уравнением
задана общим уравнением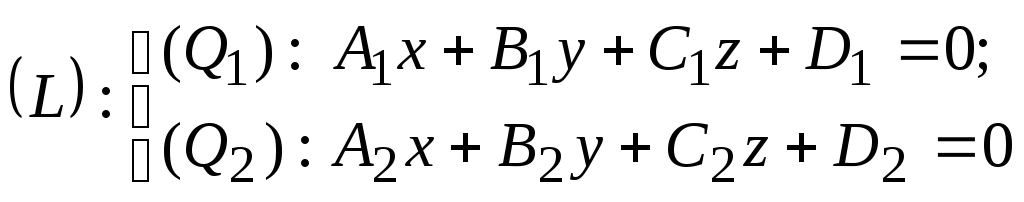 ,
а плоскость
,
а плоскость![]() уравнением
уравнением![]() .Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:
.Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:
 .
.
Если прямая
![]() задана
каноническим уравнением
задана
каноническим уравнением![]()
![]() ,
,
а плоскость
![]() уравнением
уравнением![]() ,
то поступают по следующей
,
то поступают по следующей
схеме:
– переходят
от канонического уравнения прямой к
параметрическому, т.е. записывают
уравнение прямой в виде
 ;
;
– полученные выражения подставляют в уравнение заданной плоскости
и
находят параметр
![]() :
:![]() .
.
Рассмотрим возможные случаи:
1) если
выполняются условия
 ,
то прямая не пересекает плоскость
(прямая параллельна плоскости);
,
то прямая не пересекает плоскость
(прямая параллельна плоскости);
2) при
условиях
 прямая лежит на плоскости;
прямая лежит на плоскости;
3) если
![]() ,
прямая пересекает плоскость в одной
точке.
,
прямая пересекает плоскость в одной
точке.
– вычисляют
координаты точки пересечения, подставив
найденное значение
![]() в параметрическое уравнение прямой
в параметрическое уравнение прямой
 .
.
г)
Угол
между прямой и плоскостью.
Пусть дана плоскость
![]() с нормальным вектором
с нормальным вектором![]() и пересекающая ее прямая
и пересекающая ее прямая![]() с направляющим вектором
с направляющим вектором
![]() (Рис.
53).
(Рис.
53).

![]()
![]()
![]()
![]()
![]()
![]() Рис.
53.
Угол между
прямой
Рис.
53.
Угол между
прямой
и плоскостью.
![]()
Угол
![]() является углом между прямой
является углом между прямой![]() и плоскостью
и плоскостью![]() .
Угол между нормальным вектором плоскости
и прямой обозначим через
.
Угол между нормальным вектором плоскости
и прямой обозначим через![]() .
Из рисунка видно, что
.
Из рисунка видно, что![]() .
Следовательно,
.
Следовательно,
![]()
![]() .
.
Сл1.
Если прямая
перпендикулярна плоскости (![]()
![]() ),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:
),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:
![]() .
.
Сл2.
Если прямая
параллельна плоскости (![]() ),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (
),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (![]() ),
следовательно,условие
параллельности прямой и плоскости:
),
следовательно,условие
параллельности прямой и плоскости:
![]() .
.
