2. Эллипс.

О3. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек и, называемыхфокусами эллипса, есть величина постоянная и равная .

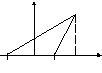
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы ибыли расположены на оси абсцисс симметрично относительно начала отсчета(Рис. 29). Пусть точка лежит на эллипсе, фокусы которого имеют координатыи.

Рис. 29. Вывод уравнения эллипса.

Расстояние между фокусами (фокусное расстояние) равно . Согласно определению эллипса имеем. Из треугольниковипо теореме Пифагора найдем

и ,

соответственно. Следовательно, согласно определению имеем

или .

Возведем обе части равенства в квадрат, получим

.

Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим . Раскроем разность квадратов. Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно

перейдет в уравнение . Вновь возведем обе части равенства в квадрат. Раскрывая все скобки в правой части уравнения, получим. Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим. Введем обозначение для разности, стоящей в скобках. Уравнение принимает вид. Разделив все члены уравнения на величину, получаемканоническое уравнение эллипса: . Если , то эллипс вытянут вдоль оси, при выполнении противоположного неравенства – вдоль оси(при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точкапринадлежит эллипсу, то ему принадлежат и точки,и, следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с координатными осями:

, т.е. точками пересечения эллипса с осью абсцисс будут точки и;

, т.е. точками пересечения эллипса с осью ординат будут точки и(Рис. 30).

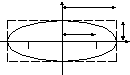
О4. Найденные точки называются вершинами эллипса.

Рис. 30. Вершины, фокусы и параметры

эллипса.

О5. Если , то параметрназывается большой, а параметр –малой полуосями эллипса.

О6. Эксцентриситетом эллипса называется отношение фокусного расстояния к большой полуоси эллипса .

Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству . Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси. Если, тои эллипс вырождается в окружность. Если, тои эллипс вырождается в отрезок.

Пример 1. Составить уравнение эллипса, если его большая полуось , а его эксцентриситет.

Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр :. Зная параметр, можно вычислить малую полуось эллипса. Следовательно, каноническое уравнение заданного эллипса имеет вид:.