Тема: Аналитическая геометрия на плоскости и в пространстве Лекция № 7 “Прямая на плоскости. Основные задачи”

1. Общее уравнение прямой.

Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами ипо этой плоскости порождает линию.

О1. Любое соотношение (имеющее смысл в области вещественных чисел), где некоторое выражение, связывающее переменные величиныи, называетсяуравнением с двумя неизвестными, которое определяет линию. Точки, принадлежащие линии, удовлетворяют приведенному соотношению, а точки вне линии – не удовлетворяют.

О2. Порядок линии определяется по высшему показателю степени переменных иили по сумме показателей степени в произведении этих величин.

Пример 1. а) – линия первого порядка; точкаудовлетворяет этому соотношению, а точка, например,– ему не удовлетворяет;

б) – линия восьмого порядка;

в) и– линии второго порядка.

Рассмотрим другое определение линии:

О2. Геометрическое место точек, координаты которых удовлетворяют уравнению , называется линией, а само уравнение – уравнением линии.

О3. Общим уравнением прямой называется уравнение первого порядка вида .

Рассмотрим частные случаи этого уравнения:

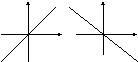
а) – прямая проходит начало системы координат(Рис. 20)

Рис. 20. Прямая, проходящая

через начало координат.

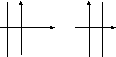
б) – прямая проходит параллельно оси ординат(Рис. 21)

Рис. 21. Прямая, проходящая параллельно

оси ординат .

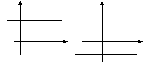
в) – прямая проходит параллельно оси абсцисс(Рис. 22)

Рис. 22. Прямая, проходящая

параллельно оси абсцисс .

2. Виды уравнений прямой.

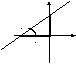
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой , в котором коэффициент. Разрешим общее уравнение прямой относительно переменной:. Обозначим черези, тогда уравнение примет вид, которое называетсяуравнением прямой с угловым коэффициентом. Выясним геометрический смысл параметров и. При, т.е. параметрпоказывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При, т.е. прямая отсекает на оси абсцисс отрезок(Рис. 23).

,

Рис. 23. Отрезки, отсекаемые прямой на

координатных осях.

Из рисунка видно, что , т.е.угловой коэффициент определяет тангенс угланаклона прямой к положительному направлению оси абсцисс .

2. Уравнение прямой в отрезках. Пусть в общем уравнении прямой параметр . Выполним следующие преобразования

; .

Обозначим через и, тогда последнее равенство перепишется в виде, которое называетсяуравнением прямой в отрезках. Выясним геометрический смысл величин и(Рис. 24). При , т.е. параметрпоказывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При, т.е. прямая отсекает на оси абсцисс отрезок. Это означает, что прямая проходит через две точкии.

Рис. 24. Отрезки, отсекаемые прямой на

координатных осях.

, ,

Пример 2. Построить прямую (самостоятельно).

3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой , которая проходит через две известные точкии. Так как точкиилежат на прямой, то их координаты удовлетворяют общему уравнению прямой, т.е. выполняются равенстваи. Вычтем первое из этих равенств из общего уравнения прямой и из второго равенства:

,

.

Пусть , тогда полученные равенства можно преобразовать к виду

, .

Отсюда находим, что или. Полученное уравнение называетсяуравнением прямой, проходящей через две заданные точки и.

Пример 3. Составить уравнение прямой, проходящей через точки и(самостоятельно).

4. Уравнение прямой, проходящей через заданную точку параллельно заданному вектору (каноническое уравнение прямой). Пусть прямая проходит через заданную точку параллельно вектору .

О4. Вектор называется направляющим вектором прямой.

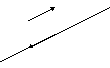
Возьмем на прямой произвольную точку и создадим вектор (Рис. 25).

Рис. 25. Прямая, проходящая через

данную точку параллельно направ-

ляющему вектору.

В силу того, что вектора и коллинеарны, то воспользуемся первым условием коллинеарности: отношения соответствующих проекций равны между собой .

О5. Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо кано-ническим уравнением прямой.

5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру , то получимпараметрическое уравнение прямой .
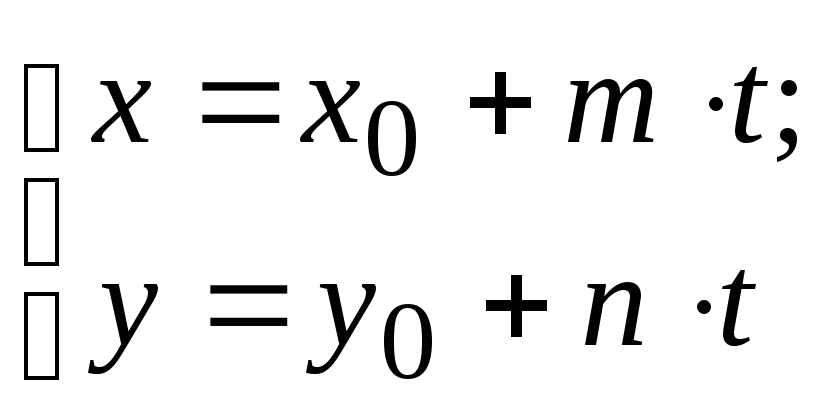