2.1.3. Пример затухающих колебаний

Рассмотрим случай, когда в подвеске имеется демпфирование (рис.2.10). Примем при расчетах массу m = 50000 кг, жесткость пружиныс = 110⁷ Н/м. Коэффициент сопротивления демпфера положим равным= 40000 Н/(м/с).

Вычисляем согласно (2.13) значения kи 2b:

k = 14,142,,

т. е. b= 0,4 иb < k, следовательно, в данном примере имеем случай 1 (малое сопротивление).

Частота затухающих колебаний

k^* = = 14,136 c^–1

меньше, чем частота собственных колебаний k. Период затухающих колебанийТ^*= 0,445 с, напротив, больше, чемТ = 0,444 с.

Рис. 2.10 Расчетная схема затухающих колебаний с демпфированием

Рис. 2.11 График затухающих колебаний

Декремент затухания (2.18) равен

0,915.

Зададим начальные условия движения: при t = 0 z₀ = 0,  =  0,1 м/с. Тогда, согласно (2.17) находим решение:

.

График затухающих колебаний показан на рис. 2.11.

2.1.4 Вынужденные колебания при отсутствии сопротивления

В задачах механики транспортных средств основной причиной возникновения вынужденных колебаний являются неровности пути. В машинных агрегатах и механизмах они возникают в результате неточной балансировки вращающихся частей машин (коленчатых валов, маховиков, турбинных дисков) либо при наличии периодически изменяющихся сил давления пара или газов в цилиндрах двигателя и т.д.

В теории колебаний возмущающей называется сила, приложенная к материальной точке и заданная как непрерывная функция времени. Простейшей является возмущающая сила, изменяющаяся по гармоническому закону. Ее проекция на направление движения имеет вид

Q_x = Q_o sin  t, (2.21)

где Q_o – наибольшая величина возмущающей силы (амплитуда силы);

 – частота возмущающей силы (частота возмущения).

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.12):

1. Восстанавливающая сила: .

2. Возмущающая сила вида (2.21).

Запишем дифференциальное уравнение движения точки:

,

Рис. 2.12 Схема вынужденных колебаний

Обозначая

, ,

получаем

(2.22)

– линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.

Его решение ищем в виде суммы

х = х₁ + х₂, (2.23)

где х₁ – общее решение однородного уравнения,

х₂ – частное решение неоднородного уравнения со специальной правой частью.

Общее решение однородного уравнения возьмем в виде (2.4):

. (2.24)

Частное решение неоднородного уравнения ищем в виде

x₂ = Сsint. (2.25)

Для определения С вычисляем вторую производную от x₂ по времени и подставляем x₂ и в (2.22). Приравнивая нулю коэффициент при sint, находим

.

Следовательно, частное решение (3.25) принимает вид

.

Согласно (2.23) получаем решение для случая, когда частота возмущения ω существенно отличается от частоты собственных колебаний k:

. (2.26)

Скорость точки получаем, вычисляя производную (2.26) по времени:

. (2.27)

Значения А и В найдем из начальных условий движения:

при t = 0 x = x₀, V = V₀.

Согласно (2.26) и (2.27) получаем

А = x₀, ,

Тогда (2.26) принимает вид

. (2.28)

Следовательно, движение представляет собой суперпозицию (наложение) собственных и вынужденных колебаний. Отметим, что при нулевых начальных условиях собственные колебания отсутствуют, а вынужденные колебания, не зависящие от начальных условий, состоят из двух гармоник: одна из них имеет частоту возмущающей силы , а другая – частоту собственных колебаний k.

В случае, если периоды и соизмеримы, движение будет периодическим, если же несоизмеримы – то апериодическим.

На рис. 2.13 показан график колебаний при Т_k = 0,444 с и Т_ = 1,25 с.

Перейдем к рассмотрению случая, когда частота возмущающей силы  близка к собственной частоте k:

.

Рис. 2.13 График вынужденных колебаний

В выражении (2.26) будем считать , но разность , и при нулевых начальных условиях получим представление решения в виде произведения двух гармоник:

. (2.29)

Первая гармоника изменяется медленно, т. к. ее период велик, период второй гармоники практически совпадает с периодом собственных колебаний:

.

Такое движение называется биением, его график показан на рис. 2.14.

Рис. 2.14 График колебаний с биением

В заключение изучим случай совпадения частоты возмущающей силы с частотой собственных колебаний: ω=k. Запишем согласно (2.28) выражение для возникающих вынужденных колебаний:

,

при ω=kполучаем неопределенность вида . Раскрывая неопределенность по правилу Лопиталя (переменной величиной являетсяω), находим:

= . (2.30)

Таким образом, при совпадении частот ωиkи отсутствии сопротивления происходит теоретически неограниченное возрастание амплитуды колебаний со временем (рис. 2.15). Это явление называетсярезонансом.

Рис. 2.15 График резонансных колебаний

В качестве примера рассмотрим возмущения вызванные неровностями пути. На рис. 2.16 показана механическая система, которая движется с постоянной скоростью v₀.

Тело массы m через подвеску, состоящую из пружины жесткости с, опирается на колесо K, массой которого пренебрегаем. Колесо движется по пути с неровностью h=h(x), которая и является источником колебаний подпрыгивания.

Рис. 2.16 Модель движущейся механической системы

Неровность пути h(x) возьмем, например, в виде гармонической функции:

, (2.31)

где x = v₀t – закон движения вдоль оси Ох;

h₀ – амплитуда неровности;

L_p – длина рельса.

Частота возникающей возмущающей силы равна

. (2.32)

На рис. 2.17 показан профиль неровности (2.31) при v₀ =20 м/с, h₀ = 0,01 м, L_p = 25 м.

Рис. 2.17 Профиль неровности пути

Пример вертикальных неровностей пути, полученный в результате путеизмерений на скорости v₀=20 м/с, показан на рис. 3.18.

Рис. 2.18 График неровностей пути (по данным путеизмерителя)

Коэффициент динамичности и АЧХ. При движении ПС частота возмущенияωпостоянно меняется (причиной этого в основном является изменение скорости движения). Поэтому необходимо определить зависимость амплитуды вынужденных колебаний от отношения частот :

,

где , – величина статической деформации пружины жесткостиспод действием силыQ₀.

Введем в рассмотрение коэффициент динамичности

, (2.33)

он показывает, во сколько раз амплитуда колебаний, происходящих под действием возмущения с частотой ω, превосходит статическую деформацию.

График зависимости коэффициента динамичности от отношения частот называется амплитудно-частотной характеристикой (АЧХ) колебаний. При отсутствии сопротивления она имеет вид, показанный на рис. 2.19.

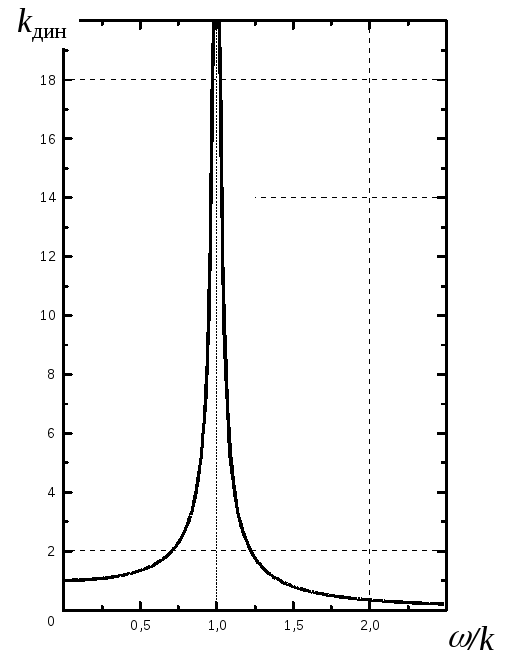
Рис. 2.19 Амплитудно-частотная характеристика (АЧХ) колебаний