2 Колебания механических систем в поле сил тяготения

Колебания механических систем в поле сил тяготения или плоскоколебательное движение механических систем рассмотрим на примере взаимодействия железнодорожного подвижного состава (ПС) и пути.

Колебания ПС возникают в силу следующих причин:

1. Колесные пары при своем движении по рельсам и стрелочным переводам совершают сложные пространственные перемещения, что вызывает колебания рам тележек, кузова и других элементов конструкции ПС.

2. Геометрическая форма рельса, его остаточный изгиб, неровности на поверхности катания, зазоры между рельсами и шпалами, шпалами и балластом, неровности в рельсовых стыках, крестовина на стрелочном переводе, пробоксовина на рельсе, вспучивание пути и т.п. вызывают соударения колес с рельсами. В результате этих соударений возникают некоторые ударные импульсы, что приводит к возникновению в стыке дополнительных динамических сил, приложенных к пути и ПС. Для ПС эта сила является источником колебаний, а для пути – причиной просадок шпал в балласте.

3. Просадки, указанные в п. 2, приводят к изменению продольного профиля пути: он становится гребнеобразным, что вынуждает колесо неравномерно перемещаться в пространстве. В результате колесо нагружается силами инерции, которые через буксовую подвеску передаются на раму тележки и другие элементы конструкции.

4. Поскольку траектория движения колес одной колесной пары по просевшим стыкам из-за различных остаточных просадок различна, наряду с вертикальными перемещениями колесная пара совершает угловые перемещения.

5. Колебания ПС могут возникать из-за неравномерного износа поверхности катания колеса или эксцентричного положения его на оси.

6. Колебания ПС могут возникать в результате его виляния при движении по рельсовой колее.

7. Колебания ПС вызываются также действием сил, возникающих при входе ПС в кривые участки пути и стрелочные кривые, от порывов ветра, аэродинамических толчков воздуха в боковую поверхность ПС при встрече поездов.

Перейдем к последовательному изучению колебаний линейных механических систем. Линейныминазываются системы, колебания которых описываются линейными дифференциальными уравнениями. В таких системах возможны два вида колебаний:свободные и вынужденные.

2.1 Свободные и вынужденные колебания

2.1.1 Свободные гармонические колебания материальной точки

Рассмотрим движение точки массы m по прямой, обозначенной как ось х (рис.2.1).

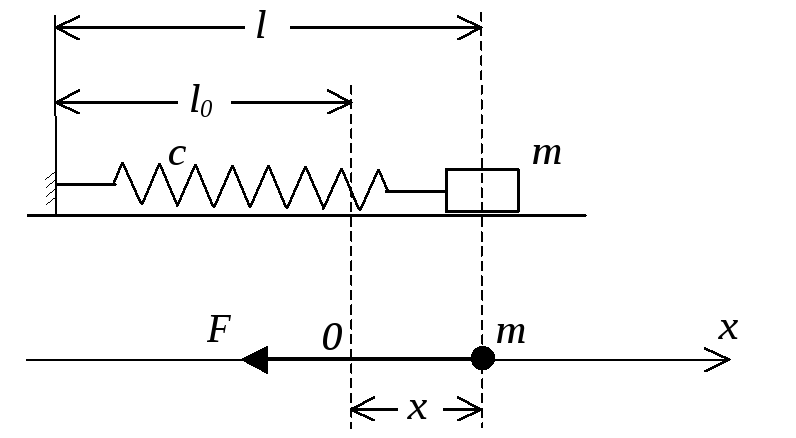
Рис. 2.1 Расчетная схема и силы действующие на массу

На точку действует только восстанавливающая сила (сила упругости пружины)

,

где с – коэффициент жёсткости пружины;

х – координата точки, равная деформации пружины l = l – l₀ (здесь l₀ – длина пружины в недеформированном состоянии, l – длина пружины в текущем состоянии).

Согласно второму закону Ньютона, запишем дифференциальное уравнение движения точки:

. (2.1)

Обозначая круговую частоту колебаний

, (2.2)

приводим дифференциальное уравнение движения к виду

, (2.3)

т. е. движение точки под действием восстанавливающей силы описывается линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

Составляем характеристическое уравнение и находим его корни: , . Поскольку корни чисто мнимые, общее решение уравнения (2.3) имеет вид

, (2.4)

где С₁,С₂– постоянные интегрирования, подлежащие определению из начальных условий движения.

Вместо С₁,С₂можно ввести другие постоянныеАиαследующим образом: ; .

Тогда решение (2.4) преобразуется к виду

,

окончательно

. (2.5)

Скорость равна первой производной координаты по времени:

. (2.5а)

Величина А называется амплитудой колебаний, – фазой колебаний, α – начальной фазой.

Амплитуда и начальная фаза выражаются через начальные условия движения (при t = 0, , ) следующим образом:

, . (2.6)

Движение материальной точки, задаваемое соотношениями 2.4), (2.5), называется свободными гармоническими колебаниями. График колебаний изображен на рис.2.2.

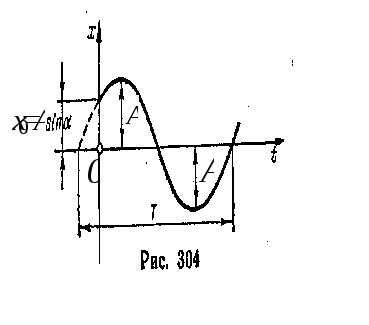
Рис. 2.2 Свободные гармонические колебания

Круговая частота k (2.2) этих колебаний называется собственной частотой механической системы, показанной на рис.2.1. Собственная частота зависит от параметров m и c, но не зависит от начальных условий движения.

Круговая частота колебаний k, измеряемая в с^–1 (то есть в радианах за секунду), и частота f, измеряемая в герцах и представляющая собой число полных колебаний за 1 секунду, связаны между собой следующим образом:

k = 2f . (2.7)

Период колебаний

(2.8)

измеряется в секундах.

Видим, что частота и период колебаний не зависят от начальных условий движения.

Рассмотрим для примера свободные гармонические колебания системы представляющей собой подрессоренное тело массы m (рис.2.3). Коэффициент жесткости пружины равенс, ее длина в недеформированном

состоянии равна l₀.

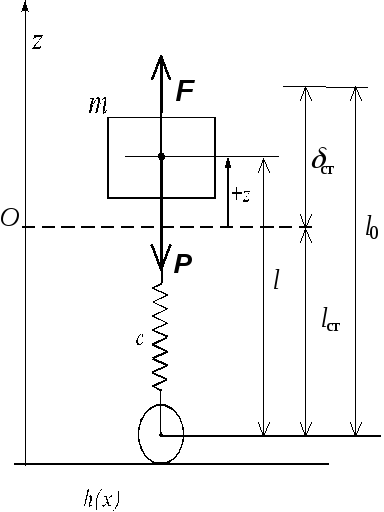
Рис. 2.3 Свободные гармонические колебания подрессоренной массы

Осадку пружины в положении равновесия обозначим _ст. Если исходить из равновесия действующих на тело силы тяжести и силы упругости , то в проекции на направленную вертикально вверх ось z

получим: – mg + c_ст = 0, откуда находим _ст = mg/c.

Уровень, соответствующий положению равновесия тела, обозначен на рис. 2.3 пунктирной линией. Начало отсчета 0 по оси z помещаем на этом уровне; если тело находится выше него, то z > 0, если ниже – то z < 0.

Примем при расчетах массу m = 50000 кг, жесткость пружиныс = 110⁷ Н/м.

Тогда круговая частота колебаний подрессоренной массы (2.2) будет равна k = 14,142 c^–1, что составляетf= 2,25 Гц. Период колебанийТ= 2/k= 0,444 с.

Зададим следующие начальные условия движения: при t = 0, z₀ = 0, V_o =  0,1 м/с, тогда согласно (2.6) находим:

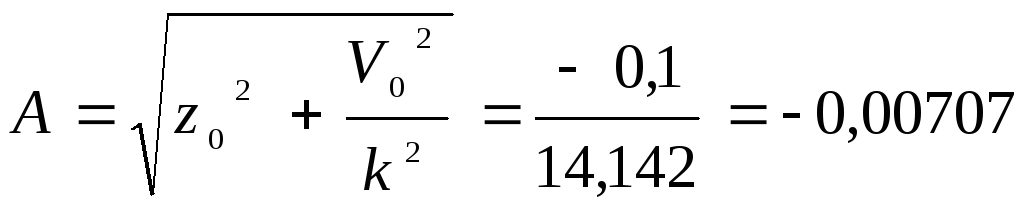м,

, т.е. α = 0.

Уравнение колебаний (2.5) приобретает вид

м,

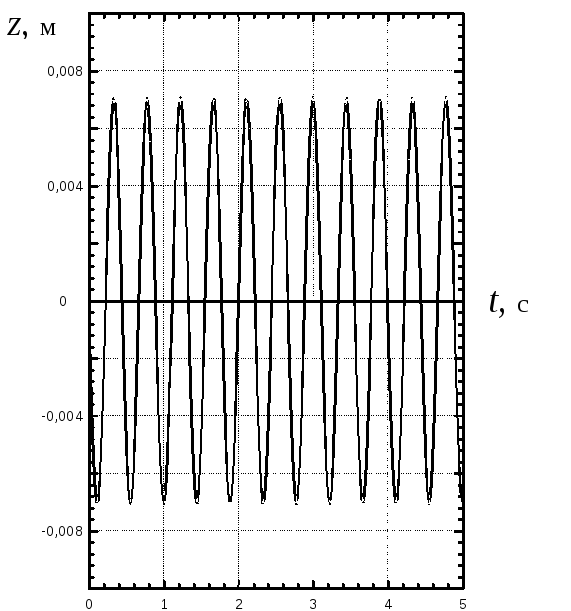график колебаний показан на рис. 2.4.

Рис. 2.4 График колебаний подрессоренной массы