Параллельное соединение пружин

При параллельном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.5), смещение тела равно деформации каждой из пружин:

. (2.9)

Рис. 2.5 Параллельное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем

,

окончательно

. (2.10)

Последовательное соединение пружин

При последовательном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда

,

,

откуда

Окончательно с учетом (2.11) получаем

. (2.12)

2. Влияние сопротивления на свободные колебания

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

1. Восстанавливающая сила (сила упругости пружины): .

2. Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .

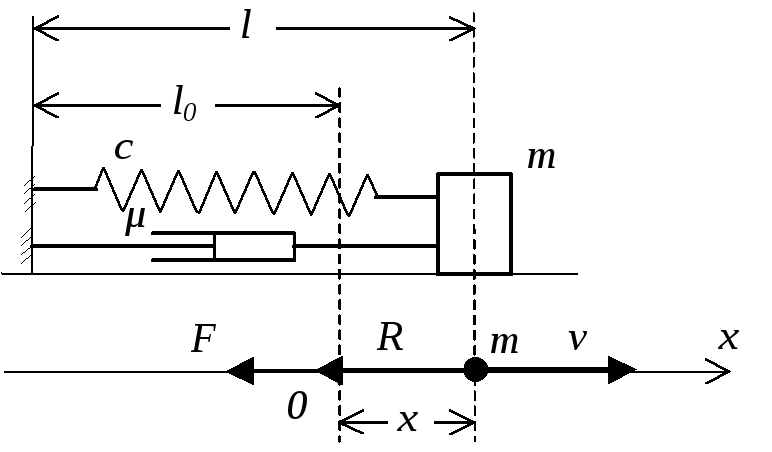
Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

обозначая

, , (2.13)

получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

Характеристическое уравнение имеет вид

, (2.15)

его корни равны

, (2.16)

где – дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.

1-й случай (малое сопротивление): b  k , D  0.

Обозначим , причем k*  k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

это затухающие колебания с частотой k^* и периодом (рис.3.8).

Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

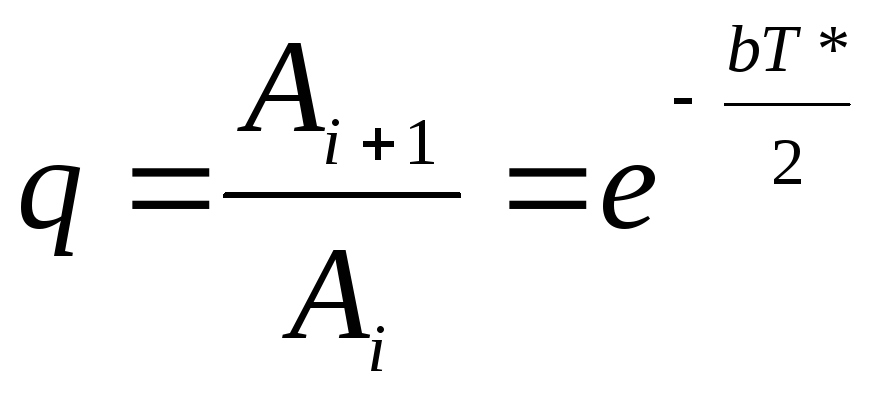< 1 (2.18)

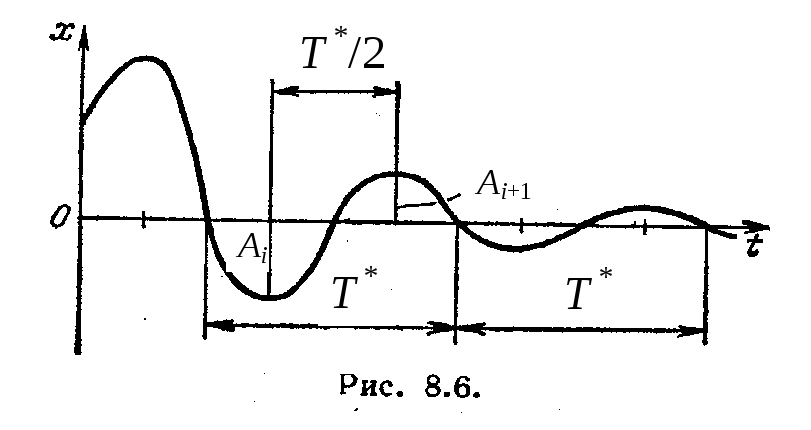
Рис. 2.8 Затухающие колебания

Часто используется также логарифмический декремент .

Таким образом, амплитуды образуют геометрическую прогрессию с показателем q, меньшим единицы.

Видим также, что наличие сопротивления приводит к уменьшению частоты колебаний (k^*  k) и к увеличению их периода (Т^* > Т).

2-й случай (граничный): b = k , D = 0.

Корни (2.16) характеристического уравнения получаются кратные, , и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т.е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b > k, D > 0.

В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

< 0, < 0,

общее решение

. (2.20)

Рис. 2.9 График затухающего апериодического движения

Здесь также получаем затухающие апериодическое движение, графики будут такие же, как и в случае b= k.