Формулы алгебры высказываний

Буквы, обозначающие высказывания, логические связки и скобки составляют алфавит языков логики высказываний: алгебры логики и исчисления высказываний.

Выражение, составленное из обозначений высказываний и связок, – логическая формула, если:

– любая переменная, обозначающая высказывание, – формула;

– если F₁ и F₂ – формулы, то выражения

также являются формулами;

– других формул, кроме построенных по правилам двух предыдущих пунктов, нет.

Пример. Представить логической формулой следующее сложное высказывание: С – « Если идет дождь, то крыши мокрые. Дождя нет, а крыши мокрые».

Решение.

Сложное высказывание C включает два простых высказывания: А – «Идет дождь», В – «Крыши мокрые». В первом предложении «Если идет дождь, то крыши мокрые» высказывания А и В соединены связкой «если…, то»: . Во втором предложении «Дождя нет, а крыши мокрые», союз «а» имеет смысл связки «и», кроме того, высказываниеА следует взять с отрицанием: . Для записи высказыванияС в виде формулы остается объединить представленные выше высказывания в одно связкой «и»: С= .

Подформулой формулы называется всякая ее часть, которая сама является формулой.

Формула называется выполнимой (опровержимой), если существует такой набор высказываний, который обращает эту формулу в истинное (ложное) высказывание.

Формула называется тождественно истинной, или тавтологией (тождественно ложной , или противоречием), если она обращается в истинное (ложное) высказывание при всех наборах значений переменных.

Пример. С помощью таблиц истинности установить, какими являются формулы и .

Решение.

Составим таблицы истинности для каждой формулы:

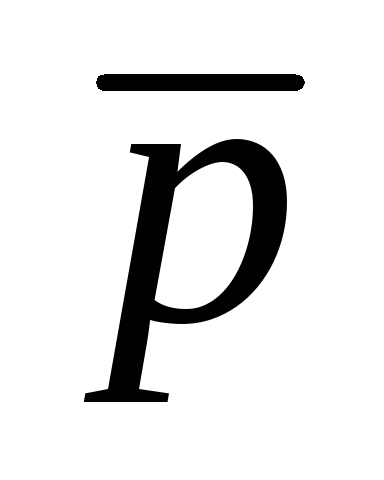
p	r		(pr)
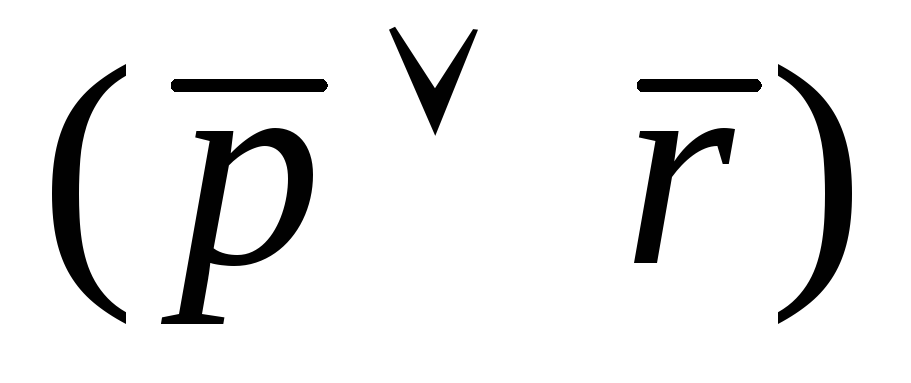
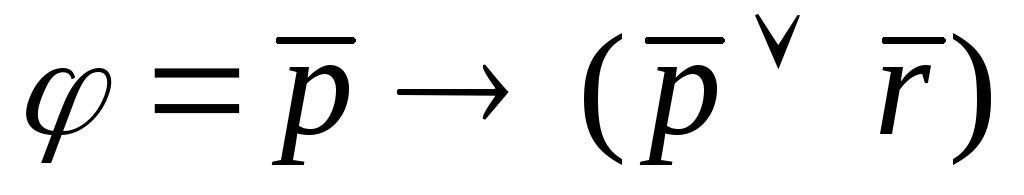
И	И	Л	И	И	Л	И
И	Л	Л	Л	И	И	И
Л	И	И	Л	Л	И	И
Л	Л	И	Л	Л	И	И

Итак, формула выполнима, а формула– тавтология.

Тавтологии играют важную роль в логике, на некоторых из них основаны способы логических умозаключений. С другой стороны, свойства логических операций также выражаются через тавтологии.

Теорема (свойства операции конъюнкции и дизъюнкции).

Следующие формулы являются тавтологиями:

1. законы идемпотентности:

2. законы коммутативности:

3. законы ассоциативности:

4. законы поглощения:

5. Законы де Моргана:

Доказательство. Докажем, что формулы идемпотентности являются тавтологиями.

X
И	И	И	И	И
Л	Л	Л	И	И

По последним двум столбцам видим, что формулы обращаются в истинное высказывание при всех наборах значений переменных, т.е. являются тавтологиями.

Формулы Х и Y называются равносильными, или эквивалентными (обозначение ), если при любых значениях переменных логические значения получающихся из формулХ и Y высказываний совпадают.

Например, по таблице истинности легко установить, что .

Замечание. Нужно различать символы «=» и «». Символ «» является символом логической операции формального языка (это необходимо и достаточно). Символ «=» не принадлежит алфавиту языка логики высказываний и говорит о равносильности формул с точки зрения их оценивания на истинность.