Элементы математической логики Лекция 5. Анализ и синтез контактных и электронных схем

5.1 Булевы функции.

5.2 Три важнейшие интерпретации булевых функций.

5.3. Примеры анализа и синтеза контактных и электронных схем.

5.3.1. Основные задачи теории релейно-контактных схем.

5.3.2. Анализ релейно-контактных схем.

5.3.3. Синтез релейно-контактных схем.

5.3.4. Схемы функциональных элементов.

5.4. Синтез логической схемы сумматора (претендентам на «5» баллов в диплом).

5.1 Булевы функции.

В анализе и синтезе контактных схем используются булевы переменные. Переменная называется булевой, если она может принимать только два значения, которые обозначают {0, 1}.

Булевой функцией называется двузначная функция от двузначных аргументов:

{0, 1}ⁿ→{0, 1}

Пример, в котором появляются булевы функции. Составным элементом нервной системы является нейрон. Это устройство предназначено для того, чтобы не пропускать слабые возбуждения и передавать достаточно регулярные и сильные.

Одна из моделей нейрона. Нейрон N имеет n входов, по которым в некоторый момент времени t могут поступать или не поступать возбуждения Если в момент t более h входов возбуждены, на выход нейрона поступает возбуждение, в противном случае оно не поступает. Обозначим входы нейрона x₁,…,x_n. Будем говорить, что вход x_i принимает значение 0 в момент t, если он не возбужден в этот момент, и значение 1, если x_i возбужден в момент t. Состояние выхода A_h(x₁,…,x_n) однозначно определяется соотношением входов и числом h. Будем считать

A_h(x₁,…,x_n) = 1, если среди значений x₁,…,x_n более h равняется 1;

A_h(x₁,…,x_n) = 0, если среди значений x₁,…,x_n не более h равняется 1

Если считать, что 0-«Л», а 1-«И», то булева функция становится истинностной функцией, а соответствующие логические операции 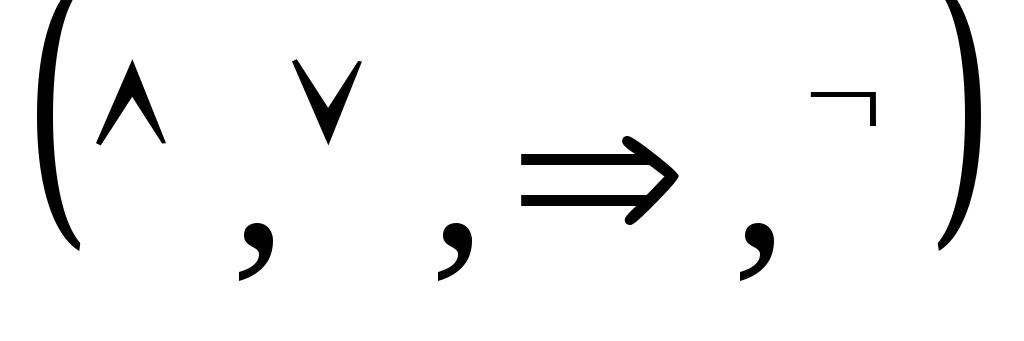справедливы для булевой функции. Для упрощения записей применяют обозначения: - отрицание,PQ – конъюнкция.

Основные булевы функции:

1. отрицание

2. конъюнкция

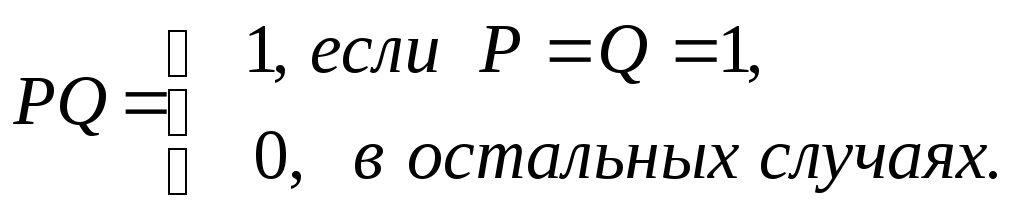
3. дизъюнкция

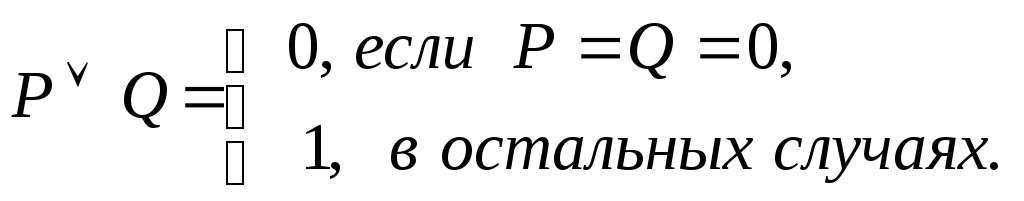
Отнесение булевых функций к основным оправдано тем, что этих трех функций достаточно для выражения любой булевой функции. Это следует из того, что система {¬,,} истинностных функций является полной. Истинностные функции не единственно возможная интерпретация булевых функций.

5.2 Три важнейшие интерпретации булевых функций.

Рассмотрим три важнейшие интерпретации булевых функций, которые представим в таблице.

Булева функция	Интерпретация булевых функций на языке
	алгебры высказываний	контактных схем	электронных схем
0 1	Л И		Сигнал низкого напряжения Сигнал высокого напряжения

5.3. Примеры анализа и синтеза контактных и электронных схем.

5.3.1. Основные задачи теории релейно-контактных схем

На возможность описания релейных схем с помощью аппарата математической логики впервые указал профессор Петербургского университета физик П. Эренфест, это было в 1910 г., а в 1936 г. этот метод применили В.И.Шестаков в СССР и Накашима в Японии. В 1938 г. в США К.Шеннон использовал булеву алгебру для синтеза и анализа релейных схем.

Подрелейно-контактной схемой понимают устройство из проводников и двухпозиционных контактов, через которое полюсы источника тока связаны с некоторым потребителем. Каждый контакт подключен к некоторому реле (переключателю) (рис. 5.1).

Реле состоит из обмотки 1, сердечника 2, якоря 3, замыкающих контактов , размыкающих контактов. Если реле срабатывает (по обмотке реле протекает ток), то якорь притягивается к сердечнику.

Рис. 5.1

При этом все подключенные к нему замыкающие контакты замкнуты, а размыкающие контакты разомкнуты, в противном случае – наоборот. На чертежах все замыкающие контакты, подключенные к реле x, обозначаются символом x, а размыкающие – символом .

Итак, каждый контакт имеет два устойчивых состояния: замкнутое и разомкнутое. Состояние каждого контакта можно рассматривать как логическую переменную х. При срабатывании реле x всем замыкающим контактам сопоставляется 1, размыкающим – 0. При отключении реле создается противоположная ситуация.

Всей схеме также ставится в соответствие логическая переменная y, которая равна 1, если схема проводит ток, и 0 в противном случае. Переменная y , соответствующая схеме, является булевой функцией от переменных , соответствующих реле. Эта функция называетсяфункцией проводимости схемы, а ее таблица – условиями работы схемы.

Две релейно-контактные схемы называются равносильными, если одна из них проводит ток тогда и только тогда, когда другая схема проводит ток, т.е. обе схемы обладают одинаковыми функциями проводимости. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов.

В теории релейно-контактных схем различают две главные задачи:

– задача анализа состоит в изучении характера работы данной схемы и ее упрощении;

– задача синтеза состоит в построении схемы по минимальной булевой функции, полученной из заданных условий работы схемы.