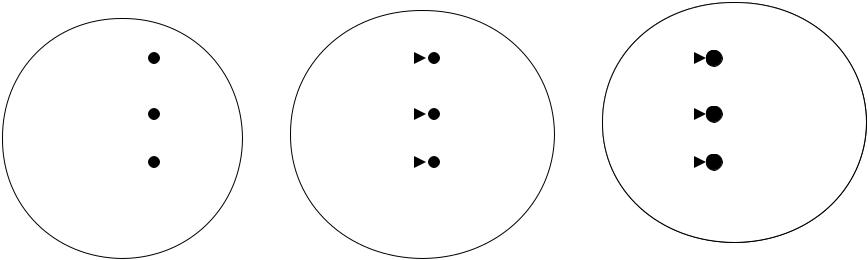
Доказательство логических следований
Умозаключения как форма мышления
Взяв за основу истинные суждения (посылки), делают выводы (умозаключения) о тех понятиях, которые фигурировали в суждениях. Связь между ними наглядно можно представить в виде схемы.
Реальный мир |
Язык |
Мышление |
|||||
А |
|
|
Аי |
|
Аיי |
||
|
|
|
|
|
|||
|
|
|
|
|
|||
Предметы |
Слова |
Понятия |
|||||
|
|
|
Вי |
|
|||
В |
|
|
|
|
Вיי |
||
|
|
|
|
||||
Знания о предметах |
Предложения |
Суждения |
|||||
|
Сי |
||||||
С |
|
|
|
Сיי |
|||
|
|
|
|
|
|||
|
Связи между |
|
|||||
Взаимосвязи |
Умозаключения |
||||||
предметов |
предложениями |
||||||
|
|
||||||
Для того чтобы из нескольких исходных суждений (посылок) получились умозаключения, надо знать правила, по которым они образуются. Истинные посылки, если соблюдены правила выводов (т.е. импликация истинна), всегда приводят к истинному заключению.
Схемы суждений
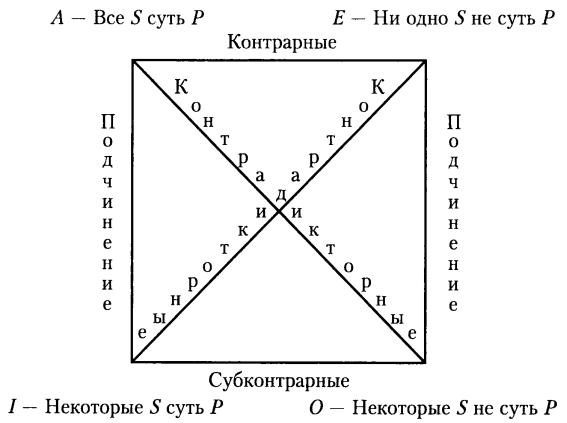
Доказательство логических следований
Непосредственные умозаключения по логическому квадрату
Изобразим классификацию суждений в виде логического квадрата. Контрадикторные суждения не могут быть одновременно истинными, и не могут быть одновременно ложными. Одно является отрицанием другого. Контрарные суждения могут быть одновременно ложными, но не могут быть одновременно истинными. Субконтрарные суждения могут быть одновременно истинными, но не могут быть одновременно ложными.
Аи → Jи, Еи → Ои
Аи → Ол Еи → Jл
Доказательство логических следований Непосредственные умозаключения
по логическому квадрату
Отношения между простыми суждениями можно изобразить на логическом квадрате или
в виде графа, в котором две верхние вершины А, E
– общие понятия (отношение противоположности), нижние О, J – частные понятия (отношение соподчинения), две правые О, E – отрицательные и две левые А, J – положительные понятия (отношение подчинения), а А,О и J,E – противоречивые понятия:
А = О, т.е. «не все S суть Р» «некоторые S не суть Р»
E=I, т.е. «неверно, что ни одно S не суть Р» «некоторые S суть Р»
.
Непосредственные умозаключения по логическому квадрату
Непосредственные умозаключения по логическому квадрату
Примеры формализации суждений
Спасибо за внимание!!!
Правила построения умозаключений по логическому квадрату: из истинности общего суждения следует истинность частного, подчинённого ему суждения (Аи → Jи, Еи → Ои), для противоречивых суждений справедлив
закон |
исключённого третьего (Аи → Ои , |
Еи→ Jи |
или Ал → Ои). |
Примеры.
А: «Все пьесы – драматургические произведения» (и), но О: «Некоторые пьесы не являются драматургическими произведениями» (л), Аи Ои , значит, Аи → Ол.
А: «Все местоимения - сказуемые» (л), но О: «Некоторые местоимения не являются сказуемыми» (и), Ал → Ои.
Е: «Ни одна окружность не является многоугольником» (и), но J: «Некоторые окружности являются многоугольниками» (л), Еи → Jл.
А: «Все союзы - сказуемые» (л), Е: «Ни один союз не является сказуемым» (и), Ал Eи .