1 2 3

Рис. 10. Нормальные кривые (1, 2, 3) при разных значениях параметра σ

(σ₁ < σ₂ < σ₃)

Любую нормальную кривую можно привести к стандартной (вычитанием μ из х_і и делением на σ). Стандартная кривая (рис. 11) имеет площадь, равную 1. Ее вершина, т.е. максимальное ордината y_max, соответствует началу прямоугольных координат, перенесенному в центр распределения, где

0,3

-3t -2t -t t 2t 3t

0,1

0,2

Рис. 11. Стандартная форма нормальной кривой (при σ = 1)

Вправо и влево от этого центра случайная величина Х может принимать любые значения, и величина каждого отклонения определяется функцией его нормированного отклоненияf(t).

Для того чтобы ордината выражала не вероятность, а абсолютные числовые значения случайной величины, т.е. выравнивающие частоты вариант эмпирических распределений, необходимо в формулу (45) внести поправку:

, (46)

Здесь λ – классовый интервал;

S_x – величина среднего квадратического отклонения эмпирического ряда распределения.

Сравнивая частоты эмпирического вариационного ряда с частотами по формуле (46), можно проверить, следуют ли эмпирическое распределение нормальному закону.

Параметры нормального распределения

Как было показано, нормальное распределение характеризуется двумя параметрами:

• средней величиной, или математическим ожиданием μ:

• дисперсией случайной величины Х:

Эмпирическая средняя стремится к математическому ожиданию случайной величины по мере увеличения числа испытаний: при небольшом числе испытаний средняя может значительно отклонятся от своего математического ожидания.

Основные свойства нормального распределения

Для нормального распределения характерно совпадение по абсолютной величине средней арифметической, медианы и моды. Равенство между этими показателями указывает на нормальность данного распределения.

Вероятность отклонения любой варианты в ту или иную сторону от средней μ на t, 2t и 3t, следующая:

Это означает, что 99,77 % от всех вариант нормально распределяющейся совокупности находится в пределах .

§ 7.7 Распределение Максвелла.

По нормальному закону распределяются многие биологические признаки, но не все: нередко встречаются и асимметричные распределения, которые, однако, не следуют закону Пуассона. Одним из таких распределений является распределение, описываемое формулой Максвелла:

Здесь – параметр распределения, определяемый через среднюю арифметическуюварьирующего признака;, гдех_i – числовые значения случайной величины Х; dx – разность между двумя смежными значениями переменной величины Х.

Признаком того, что эмпирическое распределение следует закону Максвелла, служит равенство между средним квадратическим отклонением и величиной 0,674а, т.е. S_x = 0,674 a.

§ 7.8 Измерение асимметрии и эксцесса.

Среди эмпирических распределений асимметрия и эксцесс встречаются довольно часто. Графически асимметрия выражается в виде скошенной вариационной кривой, вершина которой может находится левее или правее центра распределения. В первом случае асимметрия называется правосторонней или положительной, а во втором – левосторонней или отрицательной (по знаку числовой характеристики).

При правосторонней асимметрии ее пологая сторона находится правее (рис.14), а при левосторонней – левее центра распределения (рис.15).

Рис. 14. Положительная асимметричная кривая

Mo

Рис. 15 Отрицательная асимметричная кривая.

Mo

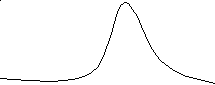
Наряду с асимметричными встречаются островершинные и плосковершинные распределения. Островершинность кривой распределения вызывается чрезвычайным накапливанием частот в центральных классах вариационного ряда, вследствие чего вершина вариационной кривой оказывается сильно поднятой вверх. В таких случаях говорят о положительном эксцессе распределения (рис. 16).

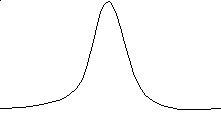
1

2

Рис. 16 Крутовершинная кривая – положительный эксцесс (1) в сравнении с нормальной кривой (2)

Кроме одновершинных встречаются и двух- и многовершинные, а также плосковершинные и двугорбые кривые, что свидетельствует о наличии у такого распределения отрицательного эксцесса (рис.17).

Величина асимметрии и эксцесса может быть различной, поэтому важно ее не только обнаружить, но измерить. Для измерения асимметрии и эксцесса используют центральные моменты распределения третьего и четвертого порядков:

(48)

1

2

Рис. 17. Плосковершинная кривая – отрицательный эксцесс (1) в сравнении с нормальной кривой (2)

При строго симметричных распределениях третьих степеней отклонений вариант от средней арифметической равна нулю и

При наличии скошенности распределения этот показатель будет иметь положительную (при правосторонней асимметрии) либо отрицательную величину (при левосторонней асимметрии), которая служит мерой асимметрии.

Показатель эксцесса, выражается формулой:

(49)

При отсутствии эксцесса . В случае положительного эксцесса этот показатель приобретает положительный знак и может иметь самую различную величину. При плосковершинности и двугорбости вариационной кривой коэффициентE_x имеет отрицательный знак; предельная величина отрицательного эксцесса равна "-2".