§ 7.3 Закон больших чисел.

Многочисленные опыты и наблюдения показали, что встречаемость ожидаемых событий приближаются к их вероятности по мере увеличения числа испытаний n.

Теоретическое обоснование закона больших чисел было дано Я. Бернулли (1713), а также П.Л. Чебышевым и другими математиками ХІХ столетия. Закон больших чисел утверждает, что частность событияА будет сколь угодно близкой к его вероятности p, если число испытаний неограниченно возрастает. В опытах с подбрасывания монеты было доказано, что частность события и его вероятность не совпадают.

Разница между ними уменьшается при увеличении числа испытаний. Можно взять сколь угодно малое число ε и сравнивать его с разницей между частностью и вероятностью события. Вероятность того, что эта разница превысит числа ε, будет стремиться к нулю при стремлении числа испытаний n к бесконечности, т.е.

§ 7.4 Биномиальное распределение.

Представим, что в отношении некоторого случайного события А производят n независимых испытаний при условии, что в каждом испытании вероятность p появления этого события постоянна. Будем учитывать только два исхода: появление события А либо противоположного ему события , тоже имеющего постоянную вероятностьq, причем .

При этих условиях, если событие А в n испытаниях появляется m раз, события будет встречаться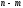раз. Вероятность любого исходанезависимо от того, в каком порядке эти события чередуются, выразится следующим уравнением Бернулли:

где 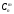– биномиальный коэффициент, определяемый по выражению:

Формула Бернулли позволяет находить вероятность того, что из n взятых наугад элементов окажется m ожидаемых.

Можно убедиться, что . Точно так же можно вычислить вероятность осуществленияm любых событий в n независимых испытаниях при условии постоянства вероятности появления события

Совокупность этих вероятностей – P_n(0), P_n(1), …, P_n(m) – называется биномиальным распределением. Можно показать, что

, (37)

Так, при n=2 возможны следующие исходы:

• результаты испытаний ;

• вероятность исходов p² pq qp q² или

При трех независимых испытаниях возможно исходов, вероятности которых распределяются следующим образом:

и т.д.

Следовательно, закон биномиального распределения выражается не только формулой Бернулли, но и формулой бинома Ньютона:

Так, например, при n = 10 возможно исхода, которые распределяются следующим образом:

Если этот ряд представить в виде графика, как показано на рис. 7, получается полином биномиального распределения, где ординаты соответствуют членам разложения бинома . Из рис. 7 видно, что биномиальная кривая строго симметрична относительно максимальной ординаты, являющейся центром биномиального распределения.

Рис. 7. Распределение вероятностей двучлена (1/2+1/2)¹⁰

Из приведенного примера также следует, что распределение вероятностей соответствует коэффициентам разложения бинома Ньютона, отнесенным к одному и тому же знаменателю, равному 2ⁿ. Биномиальные коэффициенты легко вычислить при помощи арифметического треугольника Паскаля, в котором каждая цифра находится суммированием двух цифр, стоящих над ней (табл. 22).

Сумма биномиальных коэффициентов для любой степени бинома, как это видно из табл. 22, равна 2ⁿ.

Таблиця 22

n	Биномиальные коэффициенты	2n
0	1	1
1	1 1	2
2	1 2 1	4
3	1 3 3 1	8
4	1 4 6 4 1	16
5	1 5 10 10 5 1	32
6	1 6 15 20 15 6 1	64
7	1 7 21 35 35 21 7 1	128
8	1 8 28 56 70 56 28 8 1	256
9	1 9 36 84 126 126 84 36 9 1	512
10	1 10 45 120 210 252 210 120 45 10 1	1024

Характер биномиального распределения не изменится от способа выражения исходов испытаний – в значениях вероятности или в абсолютных значениях частоты ожидаемого результата. В том и другом случае биномиальный закон выражает зависимость между частотой ожидаемого результата и числом независимых испытаний, проведенных в отношении случайного события А. Причем частота m появления ожидаемого события А в n независимых испытаний определяется его вероятностью p, которая остается постоянной в каждом отдельном испытании.

Для расчета теоретических (выравнивающих) частот вариационного ряда в формулу (37) вводят множитель:

, (39)

где p –вероятность ожидания события; ;.

Пример. Существует следующее распределение численности самок в 113 пометах лабораторных мышей:

Число самок в помете m	0	1	2	3	4	5	6	7	8
Число пометов с таки количеством самок, fi	0	1	10	17	46	28	8	3	0

В данном случае ожидаемое и противоположное события имеют одну и ту же вероятность . Число классов (без нулевых) равно семи. Сумма частот ряда, а. По треугольнику Паскаля (см .табл. 22) подбираем ряд биномиальных коэффициентовK, численно равный 1 6 15 20 15 6 1 для случая ; сумма членов рядаK равна 64. Подставляем известные величины в формулу (39):

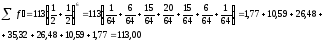
Округляя числа, получаем теоретически ожидаемые частоты ряда:

m	1	2	3	4	5	6	7
f/i	2	11	26	35	26	11	2

На моделях с известной вероятностью () ожидаемые частоты биномиального ряда легко рассчитываются по следующей формуле:

В моделях с неизвестной вероятностью значения p в формуле (39) приходится определять по средней величине полученных в опыте данных, т.е. исходить из статистической вероятности данного события. В таких случаях расчет теоретических (выравнивающих) частот биномиального ряда производят с помощью следующей формулы:

,

где N и K имеют те же значения, что и в предыдущих формулах, а p – статистическая вероятность события, определяемая отношением m/n, т.е. по средней взвешенной и.