§ 7.5 Распределение Пуассона. Параметры дискретных распределений.

Распределение Пуассона

Характер биномиальной кривой определяется двумя величинами: числом испытаний n и вероятностью p ожидаемого результата. При p =q биномиальная кривая строго симметрична и по мере увеличении числа испытаний приобретает все более плавный ход, приближаясь к своему пределу – нормальной кривой. Если , биномиальная кривая становится асимметричной и тем сильнее, чем больше разница междуp и q. Когда вероятность события очень мала и исчисляется сотыми и тысячными долями единицы, распределение частот таких редких событий в n независимых испытаний становится крайне асимметричными. Для описания такого рода распределения редких событий служит формула Пуассона:

где – наивероятнейшая частота ожидаемого события;m – частота ожидаемого события в n независимых испытаний.

Формула Пуассона позволяет определять вероятность для любых значений а от 0 до n. Чтобы формула Пуассона выражала не вероятность, а ожидаемые абсолютные частоты редких событий, ей придают следующий вид:

Здесь – теоретические ординаты кривой распределения Пуассона, или ожидаемое число случаев редкого события в каждом отдельно взятом классе испытании – 0,1,2, … и т.д.;n – число испытаний; – среднее число фактических наблюдений наблюдаемых случаев (взятое вместоа).

Распределение Пуассона – частный случай биномиального распределения. Оно, как и биномиальное распределение, приближается к нормальной кривой при возрастании числа (рис.9).

Рис. 9 График функции Пуассона для разных значений а

По закону Пуассона распределяются редкие случайные события, встречающиеся в микробиологии, радиобиологии и другие разделы современной биологии и экологии. Например, по закону Пуассона распределяются частоты спонтанных мутаций у кишечной палочки.

Параметры дискретных распределений

Биномиальное распределение характеризуется двумя параметрами:

• средним, или наивероятнейшим, числом μ ожидаемого результата и определяется по формуле: ;

• дисперсией частоты событияА в n независимых испытаниях:

Величина называют стандартным отклонением. В отличие от биномиального распределения редких событий, следующих закону Пуассона, характеризуются одним параметром – средней величиной (), так как для этого распределения характерно равенство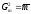. Кроме того, распределение Пуассона, как и другие асимметричные распределения, характеризуются очень высоким коэффициентом вариации.

§ 7.6 Нормальное распределение .

Случайные величины делят на дискретные и непрерывные. Случайная величина называется дискретной, если она может принимать только определенные фиксированные значения, которые обычно выражаются целыми числами. Если же случайная величина способна принимать любые числовые значения, она называется непрерывной. Очевидно, что счетные признаки относятся к дискретным случайным величинам, тогда как признаки мерные, варьирующиеся непрерывно, являются величинами непрерывными.

Закон распределения случайных величин

Функция f(x), связывающая значения х_і переменной случайной величины х с их вероятностями P_i, называется законом распределения этой величины. Закон распределения случайной величины можно задать таблично, выразить графически в виде кривой вероятности и описать соответствующей формулой.

Закон распределения дискретной случайной величины может, например, выражаться в виде биномиальной кривой и описывается формулой Бернулли, которая позволяет находить вероятные значения этой величины в серии независимых испытаний. В отношении же непрерывной случайной величины речь может идти лишь о тех значениях, которые она способна принять с той или иной вероятностью в интервале от и до.

Выдающиеся математики – А. Муавр (1733), И.Г. Ламберт (1765), П. Лаплас (1795) и К. Гаусс (1821) – установили, что очень часто вероятность P любого значения х_і непрерывно распространяющейся случайной величины х находится в интервале от х до х+dx и выражается формулой:

, (44)

где dx – малая величина, определяющая ширину интервала;

σ – стандартное рассеяние значений х_і случайной величины Х вокруг среднего μ;

μ – математическое ожидание.

Как видно из формулы (44), закон нормального распределения выражает функциональную зависимость между вероятностью P(x) и нормированным отклонением . Он утверждает, что вероятность отклонения любой вариантых_і от центра распределения μ, где , определяется функцией нормального отклоненияt. графически эта функция выражается в виде кривой вероятности, названной нормальной кривой.

Форма и положение этой кривой определяются только двумя параметрами – μ и σ. При изменении величины μ форма нормальной кривой не меняется, лишь график ее смещается вправо или влево. Изменение же величины σ влечет за собой изменение только ширины кривой:

• при уменьшении σ кривая делается более узкой за счет меньшего рассеяния вариант вокруг средней;

• при увеличении σ кривая расширяется.

Во всех случаях, однако нормальная кривая остается строго симметрична относительно центра распределения, сохраняя правильную колокообразную форму (рис.10).

Нормальная кривая с параметрами μ = 0 и σ = 1 называется нормальной или стандартизованной кривой. Она описывается следующей формулой:

, (45)