
§ 11.3 Анализ двухфакторных комплексов
Ортогональные комплексы. При образовании равномерных и пропорциональных комплексов, как и вообще при образовании многофакторных комплексов, необходимо, чтобы регулируемые факторы были независимы друг от друга. Нельзя подвергать дисперсионному анализу корреляционно связанные признаки.
Общие схемы дисперсионного анализа двухфакторных ортогональных комплексов в принципе не отличаются от описанных выше схем однофакторного дисперсионного комплекса. Анализ двухфакторных комплексов не меняет, а лишь несколько усложняет общие схемы, поскольку наряду с действием каждого фактора в отдельности приходится учитывать и их совместное действие на результативный признак. Так, для общая девиата определяется по формуле
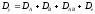
Если учитывать не два, а три регулируемых фактора A, B и C, то наряду с их индивидуальным действием возможно влияние не признак трех попарных сочетаний (АB, AC, BC), их совместное действие (АВС), а также влияние неорганизованных (случайных) факторов. Таким образом, общий компонент варьирования будет содержать восемь элементов:

При большем числе учитываемых факторов число их возможных сочетаний будет еще больше. В изучении влияния на результативный признак всех учитываемых факторов и их возможных комбинаций и заключается основная задача дисперсионного анализа. При этом не всегда необходимо учитывать все возможные сочетания организованных факторов. Этот вопрос исследователь решает в зависимости от цели исследования и принятой полноты дисперсионного анализа.
Дисперсионный анализ двухфакторных ортогональных комплексов проводят по следующей примерной схеме.
Рассчитывают девиаты: общую для всего комплекса Dy, межгрупповую Dx и остаточную De. Для этого служат формулы (11.5), (11.6) и (11.7), причем
 .
.Затем определяют факториальные девиаты:
 ; (11.23)
; (11.23)
 ; (11.24)
; (11.24)
Анализ двухфакторных пропорциональных комплексов тоже начинается с определения девиат (общей, межгрупповой и остаточной) по указанным выше формулам (11.5), (11.6) и (11.7), причем при определении Dx формула (11.7) выглядит так:
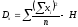 .
.
Факториальные девиаты определяют по следующим формулам:
 ; (11.25)
; (11.25)
 ; (11.26)
; (11.26)
Девиату совместного действия факторов в обоих случаях определяют по формуле
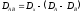 . (11.27)
. (11.27)
Как
и в предыдущих случаях, в этих формулах
повторяется величина
 ,
где xi
– варианты, входящие в состав дисперсионного
комплекса;
,
где xi
– варианты, входящие в состав дисперсионного
комплекса;
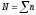 – общая численность вариант, или объем
комплекса;a
– число градаций фактора А;
b
– число градаций фактора B;
n
– количество вариант в отдельных
градациях комплекса;
– общая численность вариант, или объем
комплекса;a
– число градаций фактора А;
b
– число градаций фактора B;
n
– количество вариант в отдельных
градациях комплекса;
 – общая численность вариант в каждой
градации фактораА;
– общая численность вариант в каждой
градации фактораА;
 –общая численность вариант в каждой
градации фактораВ;
–общая численность вариант в каждой
градации фактораВ;
 – сумма вариант в градациях фактораА;
– сумма вариант в градациях фактораА;
 – сумма вариант в градациях фактораВ.
– сумма вариант в градациях фактораВ.
Определив значения девиат, переходят к установлению чисел степеней свободы, которые равны:
для общей дисперсии
 ;
;
для межгрупповой дисперсии, характеризующей влияние обоих факторов А и В на результативный признак Х
 ;
;
для внутри групповой, или остаточной, дисперсии
 ;
;
для факториальной дисперсии А
 ;
;
для факториальной дисперсии В
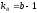 ;
;
для дисперсии совместного действия факторов А и В
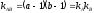
При
этом, как и предыдущих случаях, числа
степеней свободы должны находиться в
таких же количественных соотношениях,
как и соответствующие девиаты, т.е.
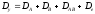 и соответственно
и соответственно .
Равенству
.
Равенству должно соответствовать равенство
должно соответствовать равенство ,
а равенству
,
а равенству – равенство
– равенство .
Эти равенства могут служить для проверки
правильности расчета девиат и чисел
степеней свободы.
.
Эти равенства могут служить для проверки
правильности расчета девиат и чисел
степеней свободы.
Отнесением девиат к соответствующим числам степеней свободы определяют значения дисперсий, а по их отношениям к величине остаточной дисперсии устанавливают дисперсионные отношения F, которые сравнивают с критическими точками Fst для соответствующих чисел степеней свободы и принимаемого уровня значимости. Нулевую гипотезу отвергают, если
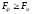 .
.
Заключительным этапом дисперсионного анализа является сведение результатов в таблицу, которая содержит следующие показатели (табл. 11.2).
Таблица 11.2
|
Вариация |
Числа степеней свободы |
Девиаты D |
Дисперсии S2 |
Дисперсионное отношение Fф |
|
По фактору А |
|
DA |
|
|
|
По фактору В |
|
DB |
|
|
|
Совместно АВ |
|
DAB |
|
|
|
Остаточная |
|
De |
|
– |
|
Общая |
|
Dy |
– |
– |
Эта таблица одновременно служит и схемой двухфакторного анализа. Обычно к ней добавляют еще два столбца, в которых приводят критические точки дисперсионного отношения Fst для 5%-ного и 1%-ного уровней значимости и соответствующих чисел степеней свободы, что облегчает выводы относительно проверки нулевой гипотезы.
Неортогональные
комплексы.
Для двухфакторных ортогональных
комплексов характерно равенство
 .
В неортогональных комплексах, т.е. в
таких, в градациях которых содержатся
неодинаковые и непропорциональные
числа вариант, это равенство нарушается,
т.е.
.
В неортогональных комплексах, т.е. в
таких, в градациях которых содержатся
неодинаковые и непропорциональные
числа вариант, это равенство нарушается,
т.е. ,
а следовательно, и
,
а следовательно, и .
Сохраняется лишь равенство
.
Сохраняется лишь равенство .
Поэтому общие девиаты рассчитывают по
тем же формулам, которые используют при
анализе равномерных и пропорциональных
комплексов.
.
Поэтому общие девиаты рассчитывают по
тем же формулам, которые используют при
анализе равномерных и пропорциональных
комплексов.
Факториальные
девиаты (DA,
DB
и DAB)
рассчитывают в два этапа. Сначала находят
значения некорректированных девиат,
обозначаемыми здесь символами
 ,
, и
и .
Сумма этих девиат равна некорректированной
общей девиате
.
Сумма этих девиат равна некорректированной
общей девиате .
Корректируя неисправленные девиаты,
получают девиаты исправленные, т.е. не
смещенные относительно равенства
.
Корректируя неисправленные девиаты,
получают девиаты исправленные, т.е. не
смещенные относительно равенства .
Коррекцию девиат производят умножением
их на поправочный коэффициент
.
Коррекцию девиат производят умножением
их на поправочный коэффициент .
Дальнейший ход анализа проводят по
обычной для двухфакторных комплексов
схеме, описанной выше.
.
Дальнейший ход анализа проводят по
обычной для двухфакторных комплексов
схеме, описанной выше.
Неисправленные девиаты определяют по следующим рабочим формулам:
 ; (11.28)
; (11.28)
 ; (11.29)
; (11.29)
 ; (11.30)
; (11.30)
 . (11.31)
. (11.31)
В этих формулах
 ,
,
 и
и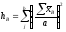 ,
,
где
 – групповые средние;
– групповые средние; – сумма групповых средних для каждой
из градаций фактораА;
– сумма групповых средних для каждой
из градаций фактораА;
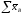 – сумма групповых средних для каждой
из градаций фактораВ;
а
– число градаций фактора А; b
– число градаций фактора В
(в группах А);
n
– численность вариант в отдельных
градациях комплекса;
– сумма групповых средних для каждой
из градаций фактораВ;
а
– число градаций фактора А; b
– число градаций фактора В
(в группах А);
n
– численность вариант в отдельных
градациях комплекса;
 – общая численность вариант, или объем
комплекса.
– общая численность вариант, или объем
комплекса.
Оценка силы влияния факторов. Силу влияния того или фактора или их совместного действия на результативный признак определяют с помощью следующих показателей:
 ; (11.32)
; (11.32)
 ;
(11.33)
;
(11.33)
 , (11.34)
, (11.34)
где
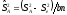 ,
,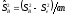 и
и – факториальные дисперсии, определяемые
по значениям межгрупповых (“неисправленных”)
и остаточной дисперсии с учетом
числа групп
a
в градациях фактора А
и числа групп b
в градациях фактора В,
а также численности вариант в группах
n.
Если комплекс неравномерный или
пропорциональный, величину n
определяют по формуле
– факториальные дисперсии, определяемые
по значениям межгрупповых (“неисправленных”)
и остаточной дисперсии с учетом
числа групп
a
в градациях фактора А
и числа групп b
в градациях фактора В,
а также численности вариант в группах
n.
Если комплекс неравномерный или
пропорциональный, величину n
определяют по формуле
 . (11.35)
. (11.35)
Знаменателем
в формулах (11.32), (11.33) и (11.34) служит величина
 .
Причем, если влияние одного из регулируемых
факторов или их совместное действие на
результативный признак не установлено,
т.е. статистически недостоверно, то этот
компонент из знаменателя исключают.
.
Причем, если влияние одного из регулируемых
факторов или их совместное действие на
результативный признак не установлено,
т.е. статистически недостоверно, то этот
компонент из знаменателя исключают.
