§ 11.2 Анализ однофакторных комплексов

Равночисленные комплексы. Дисперсионный анализ однофакторных равномерных комплексов удобно проводить по следующему алгоритму.

1. Первичные данные, подлежащие дисперсионному анализу, группируют в виде комбинационной таблицы, в которой градации организованного (регулируемого) фактора А обычно располагают по горизонтали в верхней части таблицы, а числовые значения признака Х, т.е. варианты х размещают соответственно по градациям фактора А.

2. Сгруппировав исходные данные, приступают к расчету вспомогательных величин ,и.

3. Затем переходят к расчету девиат:

• общая девиата (11.5)

• факториальная девиата (11.6)

• Остаточная девиата (11.7)

Здесь в формулах (11.5) – (11.7) 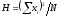, гдеx_i – варианты, входящие в состав комплекса; – общее число наблюдений, или объем комплекса;n – численность вариант x_i в каждой из градаций дисперсионного комплекса; а – число градаций фактора А.

4. Закончив расчет девиат, переходят к определению чисел свободы k, которые равны:

• для общего варьирования

• для факториального варьирования

• для остаточной вариации

Для контроля правильности расчета как девиат, так и чисел степеней свободы применяют следующее соотношение

5. Далее рассчитывают выборочные дисперсии:

• общая для всего комплекса

• межгрупповая, или факториальная

• внутригрупповая, или остаточная

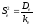
6. Наконец определяют дисперсионное отношение (при), по которому судят о действии фактора А на результативный признак. Так как фактически полученное значение дисперсионного отношения является величиной случайной, то его необходимо сравнить с табличным (стандартным) значением критерия ФишераF_st для принятого уровня значимости α и чисел степеней свободы k_A и k_e. При этом число степеней свободы для большей дисперсии находят в верхней строке, а для меньшей – в первом столбце таблицы Фишера.

Нулевую таблицу отвергают и эффективность действия фактора А на результативный признак Х признают статистически достоверной, если 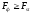; в противном случае отвергать нулевую гипотезу нельзя.

Обычно результаты дисперсионного анализа сводят в таблицу, общий вид которой представлен в табл. 11.1.

Таблица 11.1

Вариация	Числа степеней свободы	Девиаты D	Дисперсии S2	Дисперсионное отношение Fф
Факториальная		DA
Остаточная		De		–
Общая		Dy		–

Неравночисленные комплексы. Дисперсионный анализ однофакторных неравномерных комплексов, т.е. комплексов, в градациях которых содержатся разные числа вариант х_i, принципиально не отличается от анализа равномерных комплексов. Однако в связи с тем, что групповые средние неравномерных комплексов имеют разный статистический вес n_j, факториальную девиату следует вычислить по формуле

. (11.8)

Применение корреляционных таблиц. Довольно часто, особенно в выборках большого объема, отдельные варианты неоднократно повторяются, что позволяет распределять такие выборки в вариационный ряд или в ряд ранжированных значений признака. В подобных случаях удобной формой группировки исходных данных, подвергаемых дисперсионному анализу, будет корреляционная решетка, образуемая сочетанием строк и столбцов, число которых равно числу групп или классов сопряженных рядов. Классы располагаются в верхней строке и в первом (слева) столбце корреляционной таблицы; общие частоты, обозначаемые символом f_xy, распределяются по ячейкам решетки.

Классы, или значения признаков, помещаемые в верхней строке таблицы, располагаются обычно слева направо в возрастающем порядке, а в первом столбце таблицы – в убывающем порядке, т.е. сверху вниз. При этом промежутки между классами могут быть равно- и неравновеликими. При наличии неравновеликих классовых промежутков девиаты рассчитываются способом произведений по следующим формулам:

; (11.9)

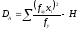, (11.10)

где ;f_x – частоты ряда Х; f_y – частоты Y; х_i – значения классовых вариант ряда Х.

Остаточную девиату определяют по формуле (11.7).

Если межклассовые промежутки рядов X и Y одинаковы, девиаты проще определять по следующим формулам:

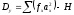; (11.11)

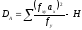, (11.12)

где ;a_x – отклонения классов от условного нуля; остальные символы те же, что и в формулах (11.9) и (11.10).

Ранговый анализ. Равночисленные (по объему) комплексы. Правильное применение дисперсионного анализа основано на предположении о нормальном распределении совокупностей, из которых извлечены выборки, входящие в дисперсионный комплекс. Если это условие, не выполняется или о характере распределения нет сведений, то применяют непараметрические методы анализа. Этот метод не требует, чтобы исходные данные были представлены абсолютными величинами; здесь допустимо использование относительных величин.

Метод основан на сравнении сумм рангов в градациях дисперсионного комплекса. Исходные данные ранжируют, т.е. располагают (в пределах градаций) в ряд по возрастающим значениям признака. Затем каждому значению признака присваивают порядковый номер, его ранг.

При наличии равномерных дисперсионных комплексов ранговый анализ проводят с помощью критерия Фридмана по формуле

, (11.13)

где – сумма рангов в каждой градации;n – численность вариант в каждой градации; а – число градаций. Полученное значение χ²_R сравнивают с критическим значением этого критерия по специальным таблицам в случаях, когда иилии. При больших значенияха и n и можно сравниватьχ²_Rф с критическими значениями χ²_st для принятого уровня значимости α и числа степеней свободы . Нулевая гипотеза, или предположение о том, что суммы рангов в градациях равны, а их различия случайны, отвергается, если.

Неравночисленные комплексы. Если в градациях дисперсионного комплекса число вариант не одинаково (неортогональный комплекс), то при обработке собранных данных следует использовать непараметрический критерий Краскелла-Уоллиса

, (11.14)

где – общее число наблюдений, или объем комплекса;n_i – численность вариант x_i в каждой из градаций дисперсионного комплекса; R_i – ранги вариант, ранжированных в общем порядке, т.е. не по отдельным градациям, а путем расположения всех вариант комплекса в один общий ряд.

Условием для непринятия нулевой гипотезы на принятом уровне значимости α будет . Приили, поэтому величинуH_ф можно сравнивать с табличным значением χ²_st.

Нулевую гипотезу отвергают, если , для принятого уровня значимостиα и числа степеней свободы .

Оценка силы влияния факторов. Метод Плохинского. После тог как достоверно установлено действие регулируемого фактора, можно измерить силу его влияния на результативный признак. Последнюю определяют ак долю межгрупповой вариации в общем варьировании результативного признака. Для измерения силы влияния предложено несколько методов. Наибольшее признание получили Плохинского (1966, 1970) и Снедекора (1961). Метод Плохинского базируется на равенстве девиат , которое осуществляется в любом дисперсионном комплексе. Показатель силы влияния, обозначаемый символомh²_x, строят следующим образом: все члены указанного равенства делят на D_y, что дает выражение

Отсюда вычисляют показатель силы влияния:

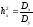или . (11.15)

Критерием достоверности этого показателя служит его отношение к своей ошибке, которую определяют по следующей приближенной формуле:

, (11.16)

где а – число градаций регулируемого фактора; N – объем дисперсионного комплекса. Нулевую гипотезу отвергают, если для принятого уровня значимостиα и чисел степеней свободы (для верхней строки таблицы) и(для первого столбца той же таблицы).

Метод Снедекора. В отличие от метода Плохинского этот метод основан на применении не девиат, а дисперсий, причем показатель силы влияния строят с учетом действия на признак не только регулируемых, но и нерегулируемых в опыте факторов, оценкой которых служит внутригрупповая дисперсия, т.е.

, (11.17)

где – исправленная межгрупповая дисперсия. S²_x и S²_e – соответственно межгрупповая (факториальная) и внутригрупповая (остаточная) дисперсии.

Если комплекс неравномерный, величину n определяют по формуле

, (11.18)

где a – число градаций регулируемого фактора; n_i – численность вариант x_i в отдельных градациях фактора; – общее число наблюдений.

Достоверность оценок силы влияния, определяемых по методу Снедекора, устанавливают посредством F-критерия Фишера, т.е. . ВеличинуF-критерия сравнивают с критическим значением этого показателю для принятого уровня значимости α и чисел степеней свободы k_x и k_e, причем последние определяют так же, как и при оценке критерия Плохинского.

Сравнение групповых средних дисперсионного комплекса. После того как достоверно установлено влияние регулируемого фактора или факторов на результативный признак, при необходимости прибегают к сравнению групповых средних друг с другом или с какой-либо другой величиной, например с контролем, стандартом, установленной нормой и т.п.

Разность между средними величинами, как описано выше, оценивают по t-критерию Стьюдента, т.е. по отношению указанной разности к ее ошибке. Этот способ, однако, неприменим к сравнительной оценке средних в дисперсионном комплексе, так как наряду с межгрупповой дисперсией на величине ошибки разности S_d между групповыми средними комплекса сказывается и влияние внутригрупповой дисперсии S²_e, величина которой зависит и от численности вариант x_i в группах, и от количества групп а, входящих в данный комплекс. Эти обстоятельства ограничивают применение критериев Стьюдента и Фишера. Поэтому в качестве ошибки разности между групповыми средними дисперсионного комплекса принят следующий показатель

, (11.19)

Для оценки разности между групповыми средними дисперсионного комплекса применяют специальные методы, созданные на базе критериев Стьюдента и Фишера. Из наиболее подходящими считают методы множественных сравнений, разработанные Дж. Тьюки ((1949) и Г. Шеффе (1953).

Метод Тьюки. Этот метод применяют для проверки нулевой гипотезы при сравнении групповых средних иравновеликих групп, т.е. при. Критерием оценки служит отношение разности сравниваемых средних к своей ошибке:

. (11.20)

Величину t_Q сравнивают с критической точкой Q_st для k_e и 5%-ного уровня значимости с учетом числа групп или градаций a регулируемого фактора А. Нулевую гипотезу отвергают, если или.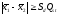

Метод Шеффе. В отличие от метода Тьюки этот метод множественных сравнений одинаково применим и к равно-, и к неравновеликим по составу группам. Критерием достоверности различий, наблюдаемых между групповыми средними дисперсионного комплекса, служат следующие отношения:

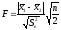(при ) (11.21)

(при 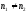) (11.22)

Нулевую гипотезу отвергают, если , гдеа – число градаций фактора А; F_st определяют по специальным таблицам Фишера для принятого уровня значимости и числа степеней свободы и, гдеN – объем дисперсионного комплекса.

Рассмотренный метод Шеффе выгодно отличается от метода Тьюки, поскольку последний применим к оценке групповых средних дисперсионного комплекса, вычисленных на разных объемах групп. Однако при сравнении средних иравновеликих групп предпочтение следует отдавать методу Тьюки.