
- •Квантовая механика и некоторые задачи фтт
- •Литература
- •Пункты программы, незнание которых влечёт оценку «2» на дифф. Зачёте.
- •Замечания.
- •Примерный план семинарских занятий.
- •Ч. Киттель. Введение в физику твердого тела. (Наука, 1978).
- •Пункты программы, незнание которых влечёт оценку «2» на экзамене.
- •Замечания.
- •Приём заданий прекращается 30 мая!
Примерный план семинарских занятий.
-
Основные термодинамические соотношения. Применение к идеальному газу с заданной теплоёмкостью
 и к газу Ван-дер-Ваальса.
и к газу Ван-дер-Ваальса. -
Микроканоническое распределение на примере осциллятора, частиц со спином ½ .
-
Каноническое распределение. Применение к осциллятору, газу дипольных молекул. Система с двумя уровнями при большой кратности вырождения верхнего уровня.
-
Химическое равновесие. Вычисление констант равновесия реакций.
-
Идеальный вырожденный ферми-газ. Эффекты внешнего поля (на примере однородного поля тяжести и осцилляторного потенциала).
-
Полупроводники (собственные и с примесями различных типов).
-
Термодинамические функции газа фотонов; уравнение адиабаты. Бозе-газ сохраняющихся частиц. Изотермы в широком интервале температур. Бозе-коденсация во внешнем поле (на примере однородного поля тяжести).
-
Простейшие трехмерные кубические кристаллические решетки и обратные к ним.
-
Фононы. Флуктуации положения атомов в кристаллической решетке (в модели Дебая).
-
Стационарные термодинамические флуктуации.
-
Корреляция флуктуаций во времени. Уравнение Ланжевена. Примеры вычисления для конкретных систем (частица в среде с трением, осциллятор с трением, электрические цепи с емкостью, индуктивностью и сопротивлением.)
-
Фазовые переходы первого рода. Применение уравнения Клапейрона-Клаузиуса. Критический радиус капли в насыщенном паре.
-
Фазовый переход второго рода на примере упорядочения бинарного сплава (приближение среднего поля).
-
Электропроводность в магнитном поле. Вычисление с помощью уравнения Больцмана в
 приближении.
приближении.
ЗАДАНИЕ № 1 (срок сдачи к первой контрольной неделе)
-
Вычислить в квазиклассическом приближении плотность энергетических состояний для частицы со спином
 в следующих ситуациях. (а) свободная
частица в яме с непроницаемыми стенками
в 1,2,3 пространственных измерениях (б)
частица в поле анизотропного гармонического
осциллятора
в следующих ситуациях. (а) свободная
частица в яме с непроницаемыми стенками
в 1,2,3 пространственных измерениях (б)
частица в поле анизотропного гармонического
осциллятора
 (в) частица с электрическим зарядом
(в) частица с электрическим зарядом
 в однородном электрическом поле
напряженности
в однородном электрическом поле
напряженности
 ,
помещенной в объем
,
помещенной в объем
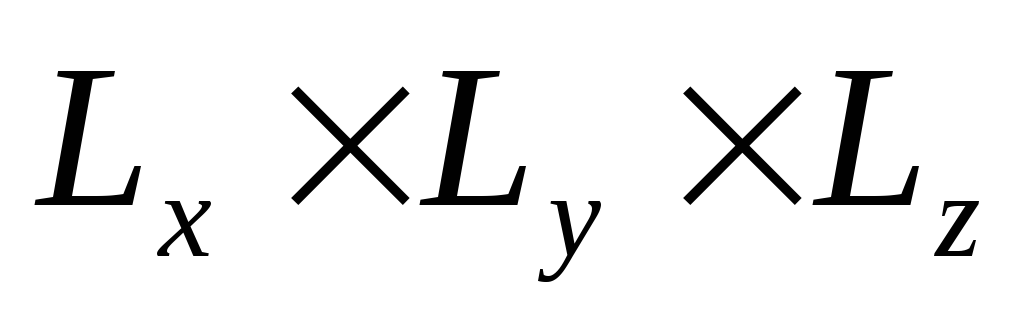 .
(9 баллов).
.
(9 баллов).
-
Плоский конденсатор с площадью пластин
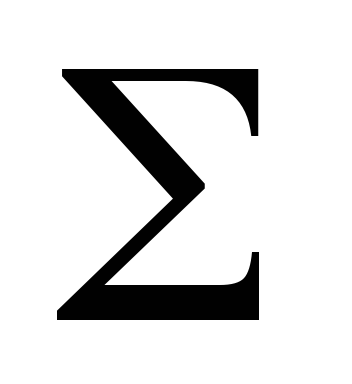 и расстоянием между ними
и расстоянием между ними
 заполнен газом нейтральных двухатомных
молекул, обладающих электрическим
дипольным моментом
заполнен газом нейтральных двухатомных
молекул, обладающих электрическим
дипольным моментом
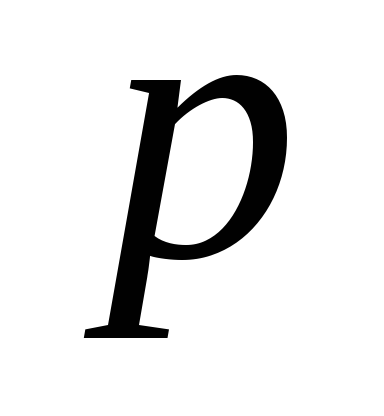 .
Число молекул
.
Число молекул
 ,
температура
,
температура
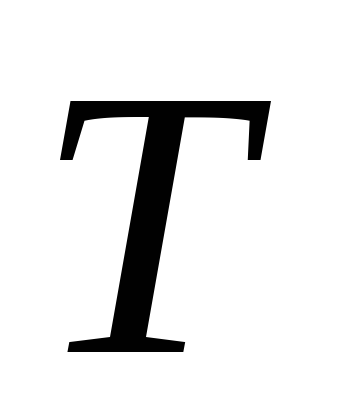 .
Сколько тепла выделится при изотермической
зарядке конденсатора до разности
потенциалов
.
Сколько тепла выделится при изотермической
зарядке конденсатора до разности
потенциалов
 ?
Найти изменение температуры газа,
если при включении электрического поля
газ был теплоизолирован. Считать, что
?
Найти изменение температуры газа,
если при включении электрического поля
газ был теплоизолирован. Считать, что
 <<1
(5 баллов).
<<1
(5 баллов).
-
Газ молекул при температуре
 находится в сосуде, ограниченном
стенками. Вычислить долю молекул,
достигающих стенки, энергия которых
превышает
находится в сосуде, ограниченном
стенками. Вычислить долю молекул,
достигающих стенки, энергия которых
превышает
 (4 балла).
(4 балла).
ЗАДАНИЕ №2 (срок сдачи 15 апреля)
-
Сильно вырожденный идеальный газ из
 нейтронов помещён в прямоугольный
сосуд с площадью основания
нейтронов помещён в прямоугольный
сосуд с площадью основания
 ,
находящийся в однородном поле тяжести.
Вычислить теплоёмкость системы и
распределение нейтронов по высоте.
Вещество сосуда непроницаемо для
нейтронов, а температура равна
,
находящийся в однородном поле тяжести.
Вычислить теплоёмкость системы и
распределение нейтронов по высоте.
Вещество сосуда непроницаемо для
нейтронов, а температура равна
 .
(5 баллов)
.
(5 баллов)
-
Электронно-дырочный спектр однослойного графена такой же, как у беспримесного полупроводника с нулевой щелью и с линейным законом дисперсии
 ,
где верхний (нижний) знак относится к
электронам
,
где верхний (нижний) знак относится к
электронам
 (дыркам
(дыркам
 ),
),
 см/с – скорость Ферми. Найти зависимость
концентрации электронов и дырок при
наложении однородного электрического
поля напряженности
см/с – скорость Ферми. Найти зависимость
концентрации электронов и дырок при
наложении однородного электрического
поля напряженности
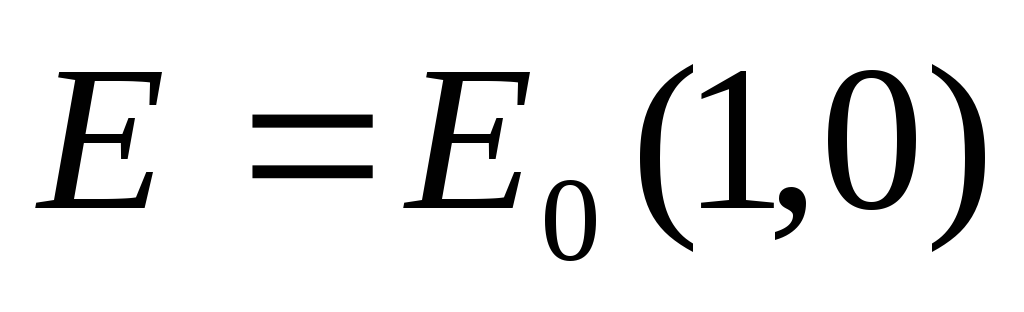 .
Образец имеет геометрические размеры
.
Образец имеет геометрические размеры
 .
(8 баллов).
.
(8 баллов).
-
3.
 атомов
атомов
 находятся в ловушке, действие которой
можно представить потенциалом
анизотропного гармонического осциллятора
находятся в ловушке, действие которой
можно представить потенциалом
анизотропного гармонического осциллятора
 .
Поперечная и продольная частоты равны
.
Поперечная и продольная частоты равны
 Гц,
Гц,
 Гц.
Спин ядра атома
Гц.
Спин ядра атома
 равен 3/2 . Показать, что этот атом является
бозоном. Вычислить температуру
бозе-эйнштейновской конденсации
равен 3/2 . Показать, что этот атом является
бозоном. Вычислить температуру
бозе-эйнштейновской конденсации
 для каждого из возможных значений
полного момента атома
для каждого из возможных значений
полного момента атома
 .
Найти теплоемкость системы ниже этой
точки и выяснить характер ее особенности
в зависимости от температуры в
окрестности
.
Найти теплоемкость системы ниже этой
точки и выяснить характер ее особенности
в зависимости от температуры в
окрестности
 .
Взаимодействием атомов между собой
пренебречь (8 баллов).
.
Взаимодействием атомов между собой
пренебречь (8 баллов).
ЗАДАНИЕ № 3 (срок сдачи 30 мая)
-
Рассчитать геометрический структурный фактор
 для гранецентрированной кубической и
объемно-центрированной кубической
структур. Зная, что при дифракции на
кристалле рентгеновских лучей с длиной
волны 1.542 ангстрема наблюдались
брэгговские углы
для гранецентрированной кубической и
объемно-центрированной кубической
структур. Зная, что при дифракции на
кристалле рентгеновских лучей с длиной
волны 1.542 ангстрема наблюдались
брэгговские углы
 и
и
 ,
определить соответствующие индексы
Миллера. Какой из двух указанных
кубических решеток принадлежит
исследуемый кристалл? Найти из
экспериментальных данных размер
элементарной ячейки (6 баллов).
,
определить соответствующие индексы
Миллера. Какой из двух указанных
кубических решеток принадлежит
исследуемый кристалл? Найти из
экспериментальных данных размер
элементарной ячейки (6 баллов).
-
Представим, что нанотехнолог изготовил молекулярное устройство, которое способно работать при температуре
 ,
причем постоянство температуры должно
поддерживаться на уровне
,
причем постоянство температуры должно
поддерживаться на уровне
 .
Сколько осцилляторов с угловой частотой
.
Сколько осцилляторов с угловой частотой
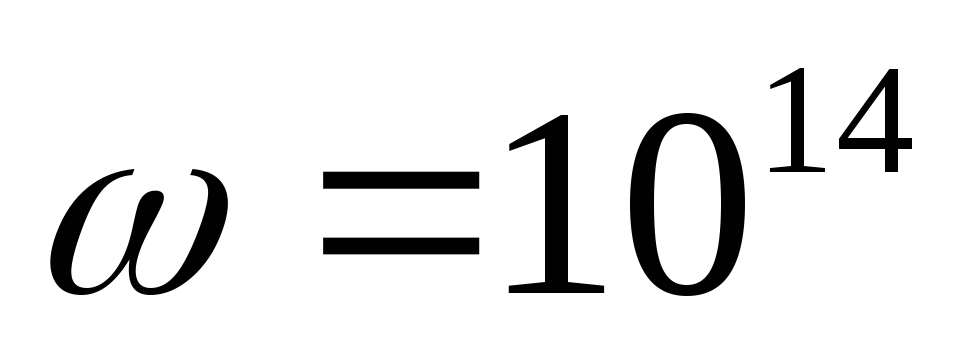 с
с потребовалось бы для изготовления
термостата, поддерживающего стабильность
температуры на таком уровне, при
потребовалось бы для изготовления
термостата, поддерживающего стабильность
температуры на таком уровне, при
 100,
200, 300 K? (2 балла).
100,
200, 300 K? (2 балла).
-
Заряженная частица движется в газе, испытывая действие однородного магнитного поля напряженности
 ,
направленного вдоль оси
,
направленного вдоль оси
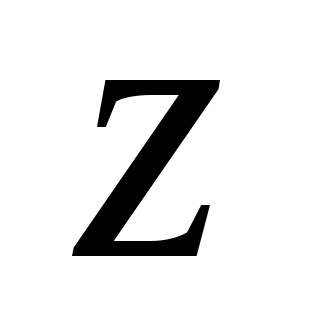 .
Сила трения, действующая на частицу со
стороны газа, пропорциональна скорости:
.
Сила трения, действующая на частицу со
стороны газа, пропорциональна скорости: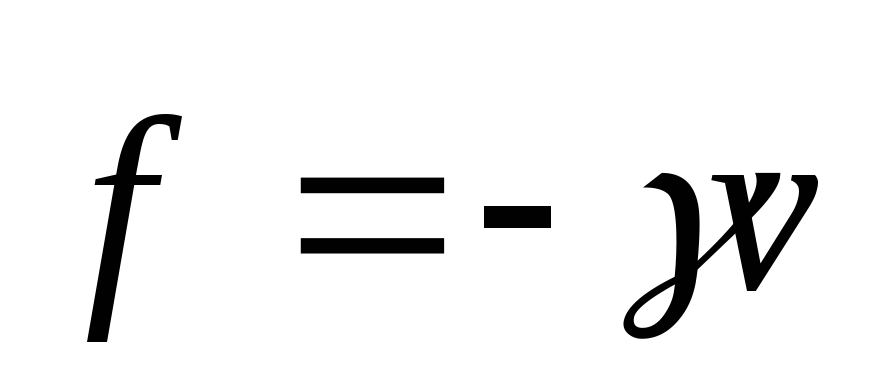 .
Температура среды
.
Температура среды
 .
Вычислить спектральные плотности
величин
.
Вычислить спектральные плотности
величин
 ,
,
 ,
,
 .
Найти коэффициенты диффузии
.
Найти коэффициенты диффузии
 и
и
 частицы
вдоль трех декартовых координат.
Вычислить корреляционную функцию
частицы
вдоль трех декартовых координат.
Вычислить корреляционную функцию
 .
(8 баллов).
.
(8 баллов).
Итого 55 баллов.
Литература.
