Литература

1. Л.Д. Ландау, Е.М. Лифшиц. Квантовая механика.

2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике, вып. 8 и 9.

3. В. Гейзенберг. Физические принципы квантовой теории. Изд. РХД, 2002 г.

4. И.И. Гольдман, В.Д. Кривченков. Сборник задач по квантовой механике.

5. В.М. Галицкий, Б.М. Карнаков, В.И. Коган. Задачи по квантовой механике.

6. Д.И. Блохинцев. Основы квантовой механики.

7. А.С. Давыдов. Квантовая механика.

8. Ч. Киттель. Введение в физику твердого тела. (Наука, 1978).

9. В.Г. Сербо, И.Б. Хриплович. Конспект лекций по квантовой механике. (РИЦ НГУ, 2010).

10. И.Ф. Гинзбург. Введение в физику твердого тела. (Издательство «Лань», 2007).

11. Г. Л. Коткин, В. А Ткаченко, О. А. Ткаченко. Компьютерный практикум

по квантовой механике. Новосибирск: Изд-во НГУ, 1996.

12. Дж. Прескилл. Квантовая информация и квантовые вычисления. Изд. РХД, (2008,2012).

13. А.А. Кожевников. Графен и квантовые вычисления: Дополнительные главы к курсу «Введение в физику твердого тела». РИЦ НГУ (2011).

ЗАДАНИЕ № 1 (срок сдачи к первой контрольной неделе)

1. Один из способов измерения энергии ультрарелятивистских электронов в накопителях состоит в том, что лазерный фотон рассеивается на электроне в направлении назад. Измеряется частота рассеянного фотона . Выразить энергию электрона через 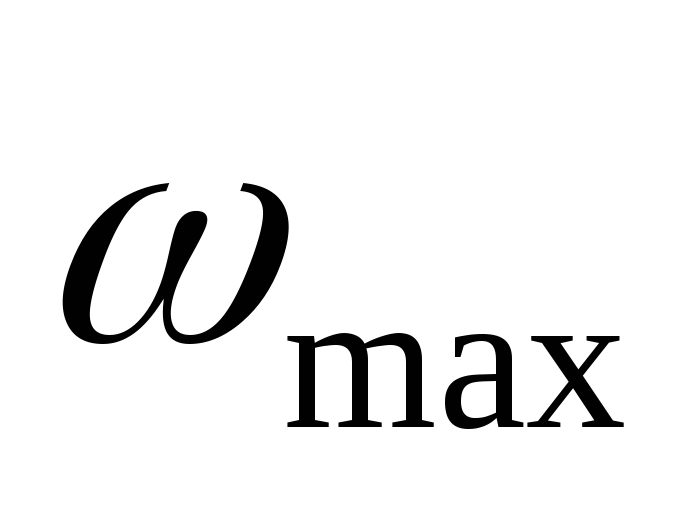. В каком частотном диапазоне окажется рассеянный фотон, если энергия электрона равна 1 ГэВ? (3 балла).

2. В опытах с конденсатами Бозе-Эйнштейна частицы первоначально находились в основном состоянии в ловушке, поле которой имеет вид поля анизотропного осциллятора . В некоторый момент времени поле выключили. Найти импульсное распределение частиц. Вычислить с его помощью отношения , . Взаимодействием частиц друг с другом пренебречь (3 балла).

3. Найти энергии и волновые функции стационарных состояний частицы в поле U(x) = -G [δ(x-a) + δ (x) + δ(x+a)]. При каких значениях a число уровней уменьшается до двух, до одного в таком поле? В предельном случае >>1 получить явные выражения для уровней энергии. Численно оценить параметр , предполагая, что частица является электроном, -функция моделирует яму глубиной 13.6 эВ, шириной 1 A, расстояние между ямами A (6 баллов).

ЗАДАНИЕ №2 (срок сдачи 25 ноября)

1. Выписать оператор Гамильтона для бесспиновой заряженной частицы в магнитном поле с векторным потенциалом. Используя уравнения Гейзенберга, найти операторы скорости и . Вычислить коммутатор. Найти соотношение неопределенностей для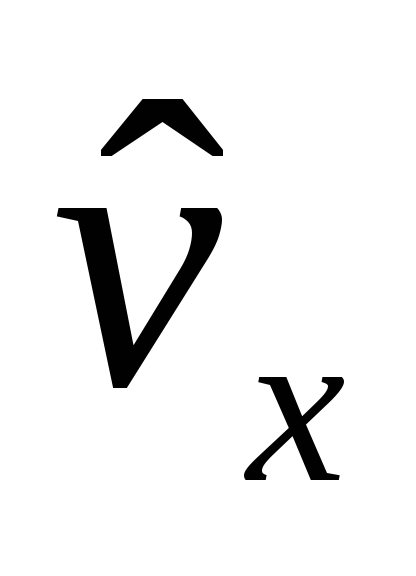 и (6 баллов).

2. Найти уровни энергии и нормированные волновые функции стационарных состояний частицы в одномерном поле с потенциальной энергией в квазиклассическом приближении (4 балла).

3. Найти энергию 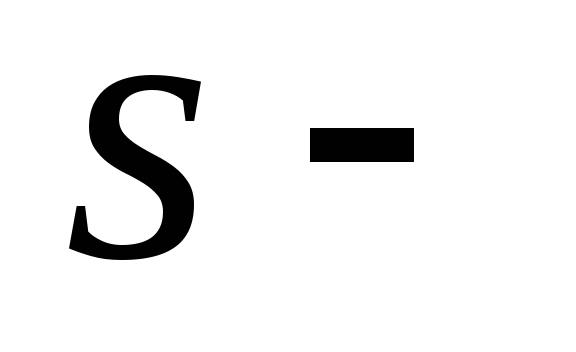волнового уровня частицы с массой поле 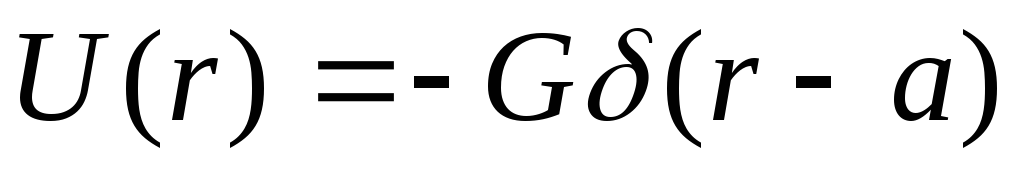предполагая, что , . Вычислить отношение вероятностей в этом состоянии (4 балла).

4. Квантовая система состоит из двух частиц со спином ½, взаимодействующих по закону 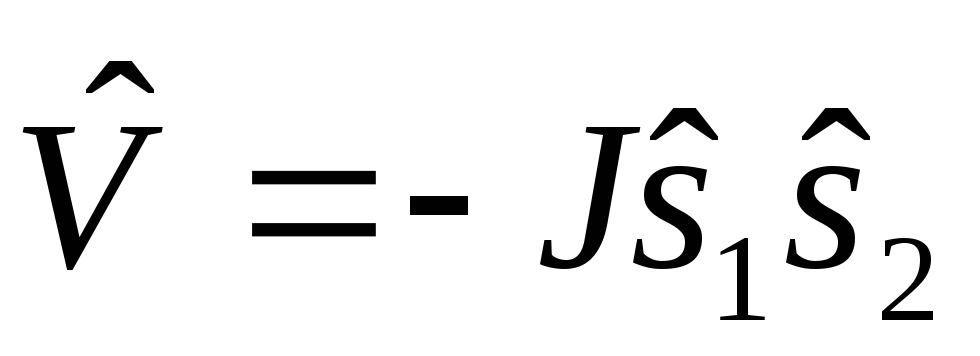. Найти уровни энергии системы во внешнем постоянном однородном магнитном поле B = (0,0,B). Выписать соответствующие выражения для спиновых волновых функций в базисе . Гиромагнитные отношения равны и 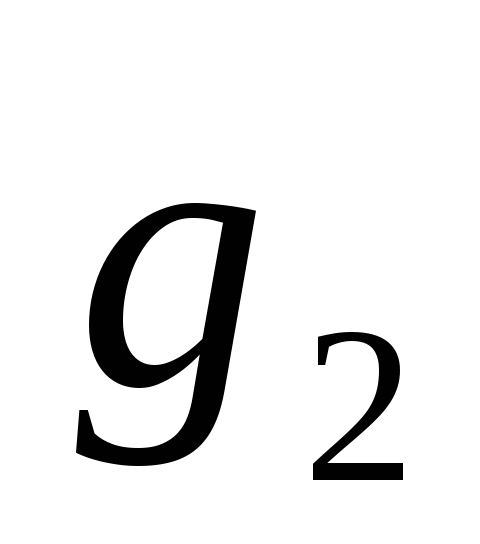. Поступательным движением пренебречь (5 баллов).

ЗАДАНИЕ № 3(срок сдачи 25 декабря).

1. Два тождественных фермиона со спином ½ находятся в одномерной потенциальной яме ширины с бесконечными стенками. Взаимодействие между ними вначале отсутствует. Выписать полные (т.е. включающие спиновую и координатную часть) волновые функции системы, отвечающие четырём низшим энергетическим уровням. Вычислить в первом порядке теории возмущений поправки к этим уровням энергии за счёт возмущения вида (6 баллов).

2. Заряженная частица находится на уровне с главным квантовым числом изотропного гармонического осциллятора. Вычислить время жизни частицы на этом уровне, обусловленное однофотонным переходом. Ответ довести до числа в предположении, что масса частицы равна массе атома рубидия, а частота осциллятора Гц. Найти угловое распределение испущенных квантов при излучении из состояний , (0,1,0) и (0,0,1) соответственно. (8 баллов)

3. Быстрые электроны рассеиваются ядром с зарядом . Найти дифференциальное сечение упругого рассеяния для случая, когда заряд ядра (a) равномерно распределен по шару радиуса и (b) равномерно распределен по поверхности сферы радиуса (6 баллов).

4. Имеется кубитов , …. Построить из них кубитовое состояние «шредингеровского кота» , последовательно применяя основные однокубитовые и двухкубитовые вентили (4 балла).

Итого 55 баллов.