
- •Глава 10. Линейные преобразования (операторы).
- •§ 1. Определение линейного преобразования.
- •§ 2. Операции над линейными преобразованиями.
- •§ 3. Преобразование матрицы линейного оператора при переходе к новому базису.
- •§ 4. Область значений и ядро линейного преобразования векторного пространства.
- •§ 5. Характеристические корни, собственные значения и собственные
- •§ 4. Приведение матрицы линейного преобразования к диагональному виду.
- •§ 7. Обобщающие примеры по теме: «Линейные преобразования»
§ 7. Обобщающие примеры по теме: «Линейные преобразования»
Набор обобщающих примеров соответствует требованиям «Семестрового плана» при изучении темы: «Линейные преобразования». Эти примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих примерах.
☺ ☻ ☺
Пример
1–1442:
Пусть задан вектор![]() =(x1,x2,x3)
линейного пространства
=(x1,x2,x3)
линейного пространства![]() .
Записано преобразование пространства:
.
Записано преобразование пространства:![]() =(x1,
x2+1,
x3+2).
Выяснить, является ли оно линейным. Если
преобразование линейное, найти его
матрицу в том же базисе, в котором заданы
векторы
=(x1,
x2+1,
x3+2).
Выяснить, является ли оно линейным. Если
преобразование линейное, найти его
матрицу в том же базисе, в котором заданы
векторы![]() и
и![]() .
.
Решение:
1). Запишем базис
пространства:
![]() =(1,0,0),
=(1,0,0),
![]() =(0,1,0),
=(0,1,0),![]() =(0,0,1).
Это значит, что произвольный вектор
линейного пространства может быть
записан в виде:
=(0,0,1).
Это значит, что произвольный вектор
линейного пространства может быть
записан в виде:![]() =x1
=x1![]() +x2
+x2![]() +x3
+x3![]() .
.
2). Пусть заданы
два произвольных вектора
![]() и
и ![]() ,
принадлежащие
,
принадлежащие ![]() .
В соответствии с определением операций
суммы векторов:
.
В соответствии с определением операций
суммы векторов:![]() =
=![]() +
+![]() =(x1+y1,x2+y2,x3+y3)
и
=(x1+y1,x2+y2,x3+y3)
и![]() =(
=(![]() x1,
x1,![]() x2,
x2,![]() x3).
x3).
3). Запишем
векторы-образы для векторов, участвующих
в доказательстве линейности
![]() :
:
![]() =
(y1,
y2+1,
y3+2)
и
=
(y1,
y2+1,
y3+2)
и ![]() =(
=(![]() x1,
x1,![]() x2+1,
x2+1,
![]() x3+2);
x3+2);
![]() =
=![]() =
(
=
(![]() +
+![]() ,
,![]() +
y2+1,
x3+y3+2).
+
y2+1,
x3+y3+2).
4). Из представленных
записей следует: требование
![]()
![]()
![]() +
+![]() - выполняется, требование
- выполняется, требование![]()
![]()
![]() - выполняется
→ преобразование
- выполняется
→ преобразование
![]() - не является линейным.
- не является линейным.
Ответ:
![]() не является линейным преобразованием.
не является линейным преобразованием.
Пример
2–1445:
Пусть имеем совокупность векторов
![]() :
:![]() =(2,3,5),
=(2,3,5),![]() =(0,1,2),
=(0,1,2),![]() =(1,0,0),
и совокупность векторов
=(1,0,0),
и совокупность векторов![]() :
:![]() =(1,1,1),
=(1,1,1),![]() =(1,1,-1),
=(1,1,-1),![]() =(2,1,2).
Доказать, что существует единственное
линейное преобразование, переводящее
совокупность векторов
=(2,1,2).
Доказать, что существует единственное
линейное преобразование, переводящее
совокупность векторов![]() в совокупность
в совокупность![]() .
Найти матрицу этого преобразования в
той же базе, в которой заданы все векторы.
.
Найти матрицу этого преобразования в
той же базе, в которой заданы все векторы.
Решение:
Замечание:
обозначим базу, в которой записаны все
векторы, и в которой должно определиться
искомое линейное преобразование, как
совокупность векторов: i=(![]() ,
,
![]() ,
,
![]() ).
).
Общая схема решения задачи:
R1
– имеем выражения:![]() =
=![]() ·
·![]() ,
,![]() =
=![]() ·
·![]() ;
;![]() ,
,![]() ,
,![]() - матрицы-столбцы.
- матрицы-столбцы.
R2
–ищем
матрицу перехода от совокупности
векторов
![]() к совокупности векторов
к совокупности векторов![]() ,
определяемую выражением:
,
определяемую выражением:![]() =
=![]() ·
·![]() ;
это выражение по форме соответствует
определению линейного преобразования
;
это выражение по форме соответствует
определению линейного преобразования![]() ,
задаваемого матрицей
,
задаваемого матрицей![]() в базе
в базе![]() .
.
R3
– в задании указано, что
матрица преобразования![]() ,
должна быть определена в базе
,
должна быть определена в базе![]() ;
это значит, что нужно матрицу
;
это значит, что нужно матрицу![]() подвергнуть трансформированию матрицей
подвергнуть трансформированию матрицей![]() перехода от базы
перехода от базы![]() к базе
к базе![]() ,
то есть:
,
то есть:![]() =
=![]() ·
·![]() .
.
R4
–определяем алгоритм
расчётов:![]() =
=![]() ·
·![]() →
→![]() =
=![]() ,
где:
,
где:![]() =
=![]() и
и![]() =
=![]() .
.
1). Из координат
векторов составим матрицы:
![]() =
= и
и![]() =
= .
Определители матриц: |
.
Определители матриц: |![]() |≠0
и|
|≠0
и|![]() |≠0
→ матрицы
|≠0
→ матрицы![]() и
и![]() невырожденные →
матрица
невырожденные →
матрица ![]() не вырожденной,
являясь произведением невырожденных
матриц.
не вырожденной,
являясь произведением невырожденных
матриц.
2). Так как совокупности
векторов
![]() и
и![]() могут использоваться в качестве баз
рассматриваемого векторного пространства
могут использоваться в качестве баз
рассматриваемого векторного пространства![]() ,
то матрица перехода от базы к базе -
невырожденная.
Это обеспечивает единственность
представления матрицы линейного
преобразования.
,
то матрица перехода от базы к базе -
невырожденная.
Это обеспечивает единственность
представления матрицы линейного
преобразования.
3). В главе 9 показано,
что матрицу перехода от базы
![]() к базе
к базе![]() для варианта-1, необходимо вычислять,
применяя выражение:
для варианта-1, необходимо вычислять,
применяя выражение:![]() =
=![]() ·
·![]() .
.
4).
Используем выражение
![]() =
=![]()
![]() .
Так как в нашем случае d
= 1, то
.
Так как в нашем случае d
= 1, то
![]() =
=![]() .
.
5)
Вычисляем матрицу
![]() =
=
 ,
где
,
где
![]() =
=![]() – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу
![]() матрицы
матрицы
![]() .
.
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
| |||||||||
|
|
|
1 |
2 |
|
|
|
0 |
|
2 |
|
|
|
0 |
1 |
|
|
| ||||||||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
0;
=
0;![]() =
=
![]()
![]() =
2;
=
2;![]() =
=![]()
![]() =
–1;
=
–1;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
5 |
|
|
|
|
2 |
|
5 |
|
|
|
|
2 |
3 |
|
|
|
| |||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
| ||||||||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
0;
=
0;![]() =
=
![]()
![]() =
–5;
=
–5;![]() =
=![]()
![]() =
3;
=
3;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
5 |
|
|
|
|
2 |
|
5 |
|
|
|
|
2 |
3 |
|
|
|
| |||||||||
|
|
|
1 |
2 |
|
|
|
0 |
|
2 |
|
|
|
0 |
1 |
|
|
| ||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
1;
=
1;![]() =
=
![]()
![]() =
–4;
=
–4;![]() =
=![]()
![]() =
2;
=
2;
6). Учитывая
результаты вычислений, можем записать:
![]() =
=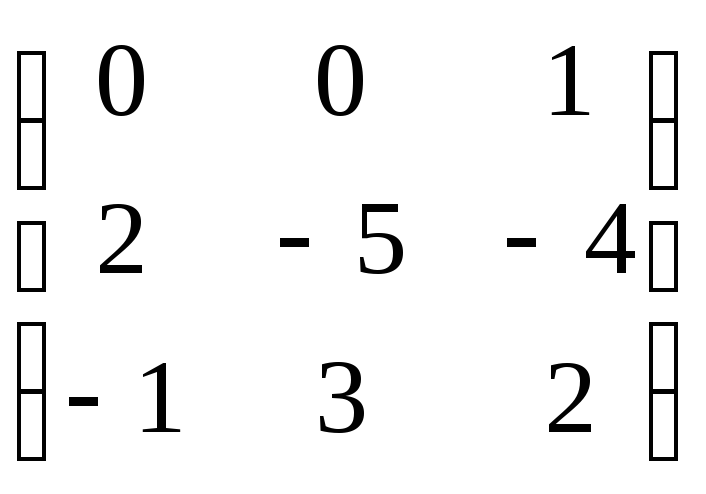 .
.
7). Вычисляем
произведение матриц:
![]() =
=![]() ·
·![]() =
= ·
· =BT,
применяя вычислительный шаблон для
произведения матриц 3-го порядка:
=BT,
применяя вычислительный шаблон для
произведения матриц 3-го порядка:
|
Столбец
|
0 |
2 |
-1 |
Столбец
|
Столбец
|
0 |
-5 |
3 |
Столбец
|
Столбец
|
1 |
-4 |
2 |
Столбец
|
|
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
-2 |
|
1 |
1 |
1 |
-1 |
|
|
1 |
1 |
-1 |
3 |
|
1 |
1 |
-1 |
-8 |
|
1 |
1 |
-1 |
-5 |
|
|
2 |
1 |
2 |
0 |
|
2 |
1 |
2 |
1 |
|
2 |
1 |
2 |
2 |
Из таблицы выписываем
матрицу:
![]() =
= -
это и есть матрица линейного преобразования
-
это и есть матрица линейного преобразования
![]() для рассматриваемого варианта для
рассматриваемого варианта:
для рассматриваемого варианта для
рассматриваемого варианта:![]() =
=![]() ·
·![]() ,
или в матричной форме:
,
или в матричной форме:
![]() =
=![]() ·
·![]() ,
или
,
или
 =
= ·
· .
.
8). Вычисляем
произведение матриц:
![]() =
=![]() =
=![]() , применяя
вычислительный шаблон для произведения
матриц 3-го порядка:
, применяя
вычислительный шаблон для произведения
матриц 3-го порядка: ![]() =
= ·
· ·
·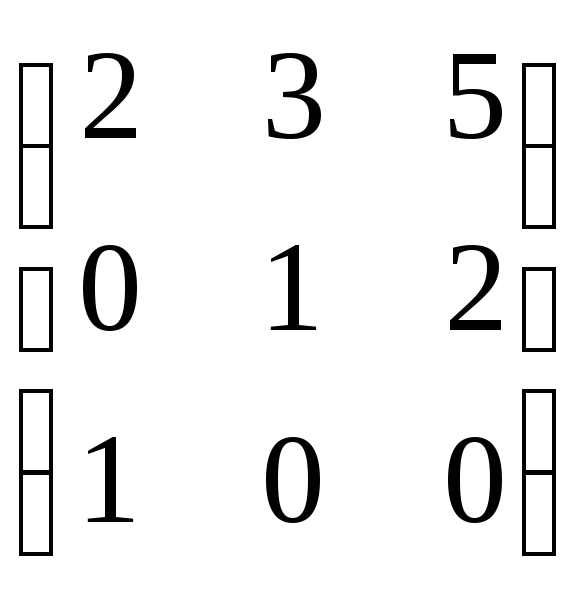 =(GC)A.
=(GC)A.
Применяем шаблон для вычисления произведения матриц: GC =T:
|
Столбец
|
1 |
3 |
0 |
Столбец
|
Столбец
|
-2 |
-8 |
1 |
Столбец
|
Столбец
|
-1 |
-5 |
2 |
Столбец
|
|
|
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
2 |
|
|
2 |
-5 |
-4 |
-13 |
|
2 |
-5 |
-4 |
32 |
|
2 |
-5 |
-4 |
15 |
|
|
-1 |
3 |
2 |
8 |
|
-1 |
3 |
2 |
-20 |
|
-1 |
3 |
2 |
-10 |
Применяем шаблон для вычисления произведения матриц: D=TA:
|
Столбец
|
2 |
0 |
1 |
Столбец
|
Столбец
|
3 |
1 |
0 |
Столбец
|
Столбец
|
5 |
2 |
0 |
Столбец
|
|
|
0 |
1 |
2 |
2 |
|
0 |
1 |
2 |
1 |
|
0 |
1 |
2 |
2 |
|
|
-13 |
32 |
15 |
-11 |
|
-13 |
32 |
15 |
-7 |
|
-13 |
32 |
15 |
-1 |
|
|
8 |
-20 |
-10 |
6 |
|
8 |
-20 |
-10 |
4 |
|
8 |
-20 |
-10 |
0 |
Из
таблицы видим матрицу D,
и записываем ответ ![]() =
= .
.
Ответ:линейное
преобразование
![]() матрица:
матрица:![]() =
= задаёт в базе
задаёт в базе![]() =
(
=
(![]() ,
,
![]() ,
,
![]() ).
).
Замечание:
использование в выражениях баз
матриц-строк приводит к матрице линейного
преобразования
![]() ,
то есть транспонированной.
,
то есть транспонированной.
Пример
3–1454:
В базе:a=(![]() ,
,![]() ,
,![]() )
определено линейное преобразование
)
определено линейное преобразование
![]() пространства
пространства ![]() ,
его матрица
,
его матрица ![]() задана в базеa,
при условии, что база представлена в
виде матрицы-столбца. Задана новая база:b=(
задана в базеa,
при условии, что база представлена в
виде матрицы-столбца. Задана новая база:b=(![]() ,
,![]() ,
,![]() ).Найти матрицу
).Найти матрицу ![]() преобразования
преобразования
![]() в базе:b.
Причём:
в базе:b.
Причём: ![]() =(8,-6,7),
=(8,-6,7),![]() =(-16,7,-13),
=(-16,7,-13),![]() =(9,-3,7);
=(9,-3,7);![]() =(1,-2,1),
=(1,-2,1),![]() =(3,-1,2),
=(3,-1,2), ![]() =(2,1,2).
Матрица
=(2,1,2).
Матрица ![]() в базеaимеет вид:
в базеaимеет вид: .
.
Решение:
1). Воспользуемся
формулой: b=![]() ·a,
где b=
·a,
где b=![]() =
=![]() ·
·![]() .
Найдём матрицу
.
Найдём матрицу![]() ,
используя записями:a=
,
используя записями:a=![]() ·
·![]() иb=
иb=![]() ·
·![]() ,
где
,
где![]() ,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем:
,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем:
![]() =
= ,
,![]() =
= .
.
2). Убеждаемся, что
матрица
![]() –
невырожденная: |
–
невырожденная: |![]() |=5.
|=5.
3). Для рассматриваемого
случая, когда
![]() ,
a,
b-матрицы-столбцы,
была получена формула для вычисления
матрицы перехода от базыaк базеb:
,
a,
b-матрицы-столбцы,
была получена формула для вычисления
матрицы перехода от базыaк базеb:
![]() =
=![]() ·
·![]() .
.
4). Вычислим
обратную матрицу
![]() ,
используя общую формулу для вычисления
обратной матрицы:
,
используя общую формулу для вычисления
обратной матрицы:
![]() =
=![]()
![]() ,
где
,
где
![]() =
1. Так как
=
1. Так как
![]() ,
то матрица
,
то матрица
![]() существует.
существует.
Вычисляем
матрицу
![]() =
=
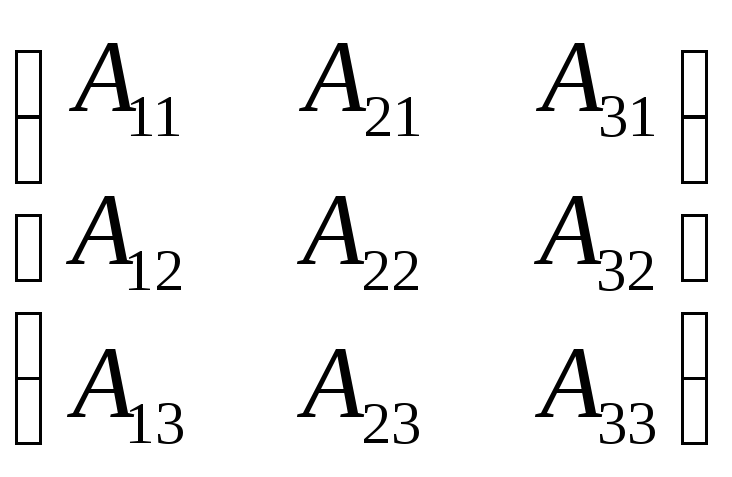 ,
где
,
где
![]() =
=![]() – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу
![]() матрицы
матрицы
![]() .
.
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
| |||||||||
|
|
|
7 |
-13 |
|
|
|
-16 |
|
-13 |
|
|
|
-16 |
7 |
|
|
| ||||||||||||
|
|
|
-3 |
7 |
|
|
|
|
|
|
|
9 |
|
7 |
|
|
|
|
|
|
|
9 |
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
10;
=
10;![]() =
=
![]()
![]() =
–5;
=
–5;![]() =
=![]()
![]() =
–15;
=
–15;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
-6 |
7 |
|
|
|
|
8 |
|
7 |
|
|
|
|
8 |
-6 |
|
|
|
| |||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
| ||||||||||||
|
|
|
-3 |
7 |
|
|
|
|
|
|
|
9 |
|
7 |
|
|
|
|
|
|
|
9 |
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
21;
=
21;![]() =
=
![]()
![]() =
–7;
=
–7;![]() =
=![]()
![]() =
–30;
=
–30;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
-6 |
7 |
|
|
|
|
8 |
|
7 |
|
|
|
|
8 |
-6 |
|
|
|
| |||||||||
|
|
|
7 |
-13 |
|
|
|
-16 |
|
-13 |
|
|
|
-16 |
7 |
|
|
| ||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
29;
=
29;![]() =
=
![]()
![]() =
–8;
=
–8;![]() =
=![]()
![]() =
–40;
=
–40;
Учитывая
результаты вычислений, можем записать:
![]() =
=![]()
 .
.
5). Вычислим
произведение матриц:
![]() =
=![]() ·
·![]() =
=![]()
 ·
· =
=![]() DB,
применяя вычислительный шаблон:
DB,
применяя вычислительный шаблон:
|
Столбец
|
10 |
-5 |
-15 |
Столбец
|
Столбец
|
21 |
-7 |
-30 |
Столбец
|
Столбец
|
29 |
-8 |
-40 |
Столбец
|
|
|
1 |
-2 |
1 |
5 |
|
1 |
-2 |
1 |
5 |
|
1 |
-2 |
1 |
5 |
|
|
3 |
-1 |
2 |
5 |
|
3 |
-1 |
2 |
10 |
|
3 |
-1 |
2 |
15 |
|
|
2 |
1 |
2 |
-15 |
|
2 |
1 |
2 |
-25 |
|
2 |
1 |
2 |
-30 |
Из
таблицы видим ответ:
![]() =
= .
.
6). Для рассматриваемого
случая:
![]() =
=![]() .
Найдём матрицу
.
Найдём матрицу
![]() =
=![]()
![]() ,
при
,
при![]() =1.
=1.
7)
Вычисляем матрицу
![]() =
=
 ,
где
,
где
![]() =
=![]() – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу
![]() матрицы
матрицы
![]() .
.
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
| |||||||||
|
|
|
2 |
3 |
|
|
|
1 |
|
3 |
|
|
|
1 |
2 |
|
|
| ||||||||||||
|
|
|
-5 |
-6 |
|
|
|
|
|
|
|
-3 |
|
-6 |
|
|
|
|
|
|
|
-3 |
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
3;
=
3;![]() =
=
![]()
![]() =
–3;
=
–3;![]() =
=![]()
![]() =
1;
=
1;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
|
|
|
| |||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
| ||||||||||||
|
|
|
-5 |
-6 |
|
|
|
|
|
|
|
-3 |
|
-6 |
|
|
|
|
|
|
|
-3 |
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
1;
=
1;![]() =
=
![]()
![]() =
–3;
=
–3;![]() =
=![]()
![]() =
2;
=
2;
*Выделим миноры:![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() ;
;![]() к элементу
к элементу![]() :
:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
|
|
|
| |||||||||
|
|
|
2 |
3 |
|
|
|
1 |
|
3 |
|
|
|
1 |
2 |
|
|
| ||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислим
алгебраические дополнения
![]() ,
,![]() ,
,![]() выделенныхминоров:
выделенныхминоров:
![]() =
=![]()
![]() =
1;
=
1;![]() =
=
![]()
![]() =
–2;
=
–2;![]() =
=![]()
![]() =
1;
=
1;
8). Учитывая
результаты вычислений, можем записать:
![]() =
= .
.
9). Вычислим:
![]() =
=![]() =
= ·
· ·
· =
(CD)N.
=
(CD)N.
Применяем шаблон для вычисления произведения матриц: CD=T:
|
Столбец
|
1 |
-18 |
15 |
Столбец
|
Столбец
|
-1 |
-22 |
20 |
Столбец
|
Столбец
|
1 |
-25 |
22 |
Столбец
|
|
|
1 |
1 |
1 |
-2 |
|
1 |
1 |
1 |
-3 |
|
1 |
1 |
1 |
-2 |
|
|
1 |
2 |
3 |
10 |
|
1 |
2 |
3 |
15 |
|
1 |
2 |
3 |
17 |
|
|
-3 |
-5 |
-6 |
-3 |
|
-3 |
-5 |
-6 |
-7 |
|
-3 |
-5 |
-6 |
-10 |
Применяем шаблон для вычисления произведения матриц: F=TN:
|
Столбец
|
3 |
-3 |
1 |
Столбец
|
Столбец
|
1 |
-3 |
2 |
Столбец
|
Столбец
|
1 |
-2 |
1 |
Столбец
|
|
|
-2 |
-3 |
-2 |
1 |
|
-2 |
-3 |
-2 |
3 |
|
-2 |
-3 |
-2 |
2 |
|
|
10 |
15 |
17 |
2 |
|
10 |
15 |
17 |
-1 |
|
10 |
15 |
17 |
-3 |
|
|
-3 |
-7 |
-10 |
2 |
|
-3 |
-7 |
-10 |
-2 |
|
-3 |
-7 |
-10 |
1 |
Из
таблицы видим матрицу F,
и записываем ответ
![]() =
= .
.
Ответ:матрицапреобразования
![]() в базе
в базе
![]() :
:![]() =
= .
.
Пример
4–1457:
Пусть преобразование
![]() в базе
в базе![]() :
(a1,a2)
задано матрицей
:
(a1,a2)
задано матрицей
![]() =
=![]() .
Преобразование
.
Преобразование
![]() в базе
в базе
![]() :(b1,b2)
задано матрицей
:(b1,b2)
задано матрицей
![]() =
=![]() .
Известно, что:
.
Известно, что:
![]() =(1,2),
=(1,2),
![]() =(2,3);
=(2,3);
![]() =(3,1),
=(3,1),
![]() =(4,2).
Найти матрицу преобразования:
=(4,2).
Найти матрицу преобразования:
![]() +
+![]() в базе
в базе
![]() .
.
Решение:
Замечание:
обозначим
базу, в которой записаны векторы
![]() ,
,![]() ,
как совокупность векторов:
,
как совокупность векторов:
![]() =
(i1,
=
(i1,
![]() ).
Все базы:
).
Все базы:
![]() ,
,![]() ,
,![]() записываем в виде матриц-столбцов.
записываем в виде матриц-столбцов.
1). Воспользуемся
формулой: b=![]() ·a,
где b=
·a,
где b=![]() =
=![]() ·
·![]() .
Найдём матрицу
.
Найдём матрицу![]() ,
используя записями:a=
,
используя записями:a=![]() ·
·![]() иb=
иb=![]() ·
·![]() ,
где
,
где![]() ,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем:
,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем: ![]() =
=![]() ,
,
![]() =
=![]() .
Так как |
.
Так как |![]() |=–1,
то матрица
|=–1,
то матрица![]() невырожденная и существует обратная
матрица
невырожденная и существует обратная
матрица![]() .
.
2). Вычислим матрицу
![]() =
=![]()
![]() ,
при
,
при![]() =–1.
Так как
=–1.
Так как
![]() =
=![]() ,
то
,
то![]() =
=![]() .
После этого можно вычислить матрицу
.
После этого можно вычислить матрицу![]() =
=![]() ·
·![]() .
Для обеспечения надёжности вычислений
воспользуемся шаблоном умножения матриц
2-го порядкаC
=
.
Для обеспечения надёжности вычислений
воспользуемся шаблоном умножения матриц
2-го порядкаC
=![]()
![]() =BT:
=BT:
|
Столбец
|
-3 |
2 |
Столбец
|
Столбец
|
2 |
-1 |
Столбец
|
|
|
3 |
1 |
-7 |
|
3 |
1 |
5 |
|
|
4 |
2 |
-8 |
|
4 |
2 |
6 |
из таблицы читаем
матрицу
![]() =
=![]() .
.
3). Запишем матрицу
преобразования
![]() в базе
в базе
![]() :
:![]() =
=![]() .
Найдём матрицу
.
Найдём матрицу
![]() =
=![]()
![]() ,
при
,
при![]() =–2,
=–2,
![]() =
=![]() получаем:
получаем:
![]() =
=![]()
![]() .
.
4). Вычислим
матрицу: ![]() =
=![]() =
=![]()
![]()
![]()
![]() =
=![]() CDN=
CDN=![]() TN,
используя вычислительный шаблон для
произведения матриц:
TN,
используя вычислительный шаблон для
произведения матриц:
|
Столбец
|
3 |
5 |
Столбец
|
Столбец
|
4 |
3 |
Столбец
|
|
|
-7 |
5 |
4 |
|
-7 |
5 |
-13 |
|
|
-8 |
6 |
6 |
|
-8 |
6 |
-14 |
|
Столбец
|
-6 |
-8 |
Столбец
|
Столбец
|
5 |
7 |
Столбец
|
|
|
4 |
-13 |
80 |
|
4 |
-13 |
-71 |
|
|
6 |
-14 |
76 |
|
6 |
-14 |
-68 |
из таблицы читаем
матрицу
![]() =
=![]()
![]() .
.
5). Матрица
преобразования:
![]() +
+![]() в базе
в базе
![]() :
:![]() =
=![]() +
+![]() =
=![]() +
+ =
=![]() .
.
Ответ: Матрица
преобразования:
![]() +
+![]() в базе
в базе
![]() :
:![]() =
=![]() .
.
Замечание:
полученный
числовой результат отличается от ответа,
представленного в задачнике: у нас
матрица
![]() ,
в задачнике – транспонированная матрица
,
в задачнике – транспонированная матрица
![]() .
.
Пример
5–1466:Найти собственные
векторы линейного преобразования
![]() ,
заданного в некотором базисе
матрицей:
,
заданного в некотором базисе
матрицей:
 .
.
Решение:
1). Составляем характеристический многочлен и находим его корни, используя свойства определителя и правила нахождения корней многочлена:
![]() =
=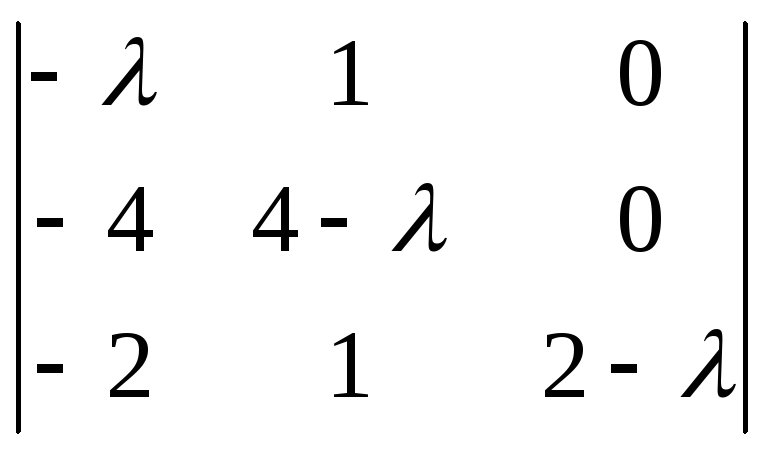 =
(2–
=
(2–![]() )
)
![]() =–
=–![]() ,
откуда корни:
,
откуда корни: ![]() =
=![]() =
=![]() =2.
=2.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:
 (A)
(A)
3).
Для собственного значения ![]() =
2 система (A)
принимает вид:
=
2 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 1). Назначаем свободными
неизвестными: ![]() =2
=2![]() ,
,
![]() =
=![]() ,
тогда
,
тогда ![]() =
=![]() ,
получаем собственный вектор:
,
получаем собственный вектор: ![]() =
(
=
(![]() ,2
,2![]() ,
,![]() )=
)=![]() (1,2,0)+
(1,2,0)+
![]() (0,0,1).
(0,0,1).
Ответ:
собственные значения: ![]() =
=![]() =
=![]() =
2; собственные векторы:
=
2; собственные векторы: ![]() =(
=(![]() ,2
,2![]() ,
,![]() ),
где
),
где ![]() ,
,![]()
0.
0.
Пример
6–1473:Найти собственные
векторы линейного преобразования
![]() ,
заданного в некоторой базе матрицей:
,
заданного в некоторой базе матрицей:
 .
.
Решение:
1). Составляем характеристический многочлен и находим его корни, используя свойства определителя и правила нахождения корней многочлена:
![]() =
= =(1–
=(1–![]() )
)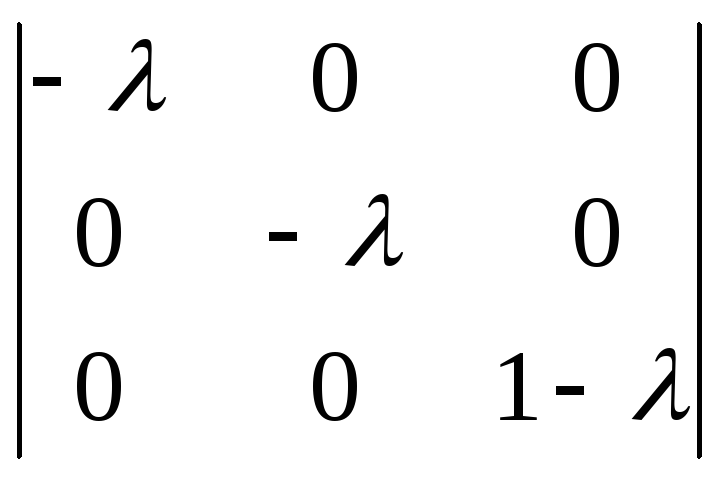 =–
=–![]() ,
,
откуда
корни многочлена ![]() :
:
![]() =
=![]() =0,
=0,
![]() =
=![]() =1.
=1.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:
 (A)
(A)
3).
Для собственного значения ![]() =
0 система (A)
принимает вид:
=
0 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более трёх
(в нашем случае 2). Назначаем свободными
неизвестными:
![]() =
=![]() ,
,![]() =
=![]() ,
,
![]() =
=![]() =0.
Найдём фундаментальную систему решений
для полученной системы:
=0.
Найдём фундаментальную систему решений
для полученной системы:
-
x1
x4
x2
x3
α1
0
0
1
0
α2
0
0
0
1
Векторы-решения
![]() и
и![]() есть ФСР для
есть ФСР для![]() =
0, тогда любойсобственный
вектор линейного преобразования можно
представить в виде:
=
0, тогда любойсобственный
вектор линейного преобразования можно
представить в виде: ![]() =
=![]() +
+![]() =
=![]() (0,1,0,0)
+
(0,1,0,0)
+![]() (0,0,1,0),
где
(0,0,1,0),
где ![]() ,
,![]() - произвольные постоянные.
- произвольные постоянные.
4).
Для собственного значения ![]() =1
система (A)
принимает вид:
=1
система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более трёх
(в нашем случае 3). Назначаем свободными
неизвестными:
![]() =
=![]()
![]() =
=![]() ,
,
![]() =
=![]() =0.
Найдём фундаментальную систему решений
для полученной системы:
=0.
Найдём фундаментальную систему решений
для полученной системы:
-
x2
x3
x1
x4
α3
0
1
1
0
α4
0
0
0
1
Векторы-решения
![]() и
и![]() есть ФСР для
есть ФСР для![]() =1,
тогда любой собственный вектор линейного
преобразования можно представить в
виде:
=1,
тогда любой собственный вектор линейного
преобразования можно представить в
виде:![]() =
=![]() +
+![]() =
=![]() (1,0,1,0)+
(1,0,1,0)+![]() (0,0,0,1),
где
(0,0,0,1),
где![]() ,
,![]() - произвольные постоянные.
- произвольные постоянные.
.
Ответ:
собственные значения:
![]() =
=![]() =0,
=0,
![]() =
=![]() =
1; собственные векторы:
=
1; собственные векторы:
![]() =
=![]() (0,1,0,0)
+
(0,1,0,0)
+![]() (0,0,1,0),
где
(0,0,1,0),
где
![]() ,
,![]() - не равны нулю одновременно,
- не равны нулю одновременно,
![]() =
=![]() (1,0,1,0)+
(1,0,1,0)+![]() (0,0,0,1),
где
(0,0,0,1),
где
![]() ,
,![]() - не равны нулю одновременно.
- не равны нулю одновременно.
Пример
7–1479:Линейное
преобразование
![]() ,
заданного матрицей:
,
заданного матрицей:
 в некотором базисе пространства
в некотором базисе пространства
![]() .Можно ли привести матрицу преобразования
.Можно ли привести матрицу преобразования
![]() к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
Решение:
1). Составляем характеристический многочлен и находим его корни, используя свойства определителя и правила нахождения корней многочлена:
![]() =
= =
(1)
=
(
=
(1)
=
(![]() –2)
–2) =
(2)
=–
(
=
(2)
=–
(![]() –2)
(
–2)
(![]() –1)
(
–1)
(![]() +4),
+4),
откуда
корни многочлена ![]() :
:
![]() =1,
=1,
![]() =2,
=2,
![]() =–4.
=–4.
Выполнены
операции:
(1):
[R3]–[R2]
и выносим за скобку определителя
множитель: (![]() –2);
меняем одновременно знаки в [C1]
и [C3].
–2);
меняем одновременно знаки в [C1]
и [C3].
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:
 (A)
(A)
3).
Для собственного значения ![]() =
1 система (A)
принимает вид:
=
1 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 2). Назначаем свободной
неизвестной: ![]() =
=![]() ,
из системы имеем:
,
из системы имеем: ![]() =
=![]() ,
,
![]() =
=![]() ,
тогда получаем
собственный вектор, приняв
,
тогда получаем
собственный вектор, приняв ![]() =1:
=1:
![]() =
(1,1,1).
=
(1,1,1).
4).
Для собственного значения ![]() =
2 система (A)
принимает вид:
=
2 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 1). Назначаем свободной
неизвестной: ![]() =
=![]() ,
,
![]() =3
=3![]() ,
из системы имеем:
,
из системы имеем: ![]() =
=![]() –
–![]() ,
тогда получаем
собственный вектор, приняв
,
тогда получаем
собственный вектор, приняв ![]() =1,
=1,
![]() =0:
=0:
![]() =
(1,1,0).
=
(1,1,0).
5).
Для собственного значения ![]() =–4
система (A)
принимает вид:
=–4
система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 2). Назначаем свободной
неизвестной: ![]() =
=![]() ,
из системы имеем:
,
из системы имеем: ![]() =
=![]() ,
3
,
3![]() =2
=2![]() ,
тогда получаем
собственный вектор, приняв
,
тогда получаем
собственный вектор, приняв ![]() =3:
=3:
![]() =
(–2,3,3).
=
(–2,3,3).
Ответ:
собственные значения:
![]() =1,
=1,![]() =2,
=2,![]() =–4;
собственные векторы:
=–4;
собственные векторы:
![]() =
(1,1,1),
=
(1,1,1),
![]() =
(1,1,0),
=
(1,1,0),
![]() =
(–2,3,3). Диагональная матрица:
=
(–2,3,3). Диагональная матрица:
 .
.
Пример
8–1482:Линейное
преобразование
![]() ,
заданного матрицей:
,
заданного матрицей:
 в некотором базисе пространства
в некотором базисе пространства![]() .Можно ли привести матрицу преобразования
.Можно ли привести матрицу преобразования
![]() к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
Решение:
1). Составляем характеристический многочлен и находим его корни, используя свойства определителя и правила нахождения корней многочлена:
![]() =
= =
(1)
=
=
(1)
= =
(2)
→
=
(2)
→
![]() =(4–
=(4–![]() )·
)· –1·
–1· =
(3)
→
=
(3)
→
![]() =(4–
=(4–![]() )·
)· –
– =
=![]() +
+![]() = (4) →
= (4) →
Выполнены
операции:
(1):
[R2]–[R4]·5;
[R3]–[R4]·6.
(2):
применяем разложение определителя по
первому столбцу. (3):
в первом слагаемом: [R2]+[R4]·2;
во втором слагаемом [R3]+[R1]·2;
(4):
далее вычислим отдельно ![]() и
и ![]() .
.
![]() =
(1)
=
(
=
(1)
=
(![]() –4)·
–4)· =
(2)
=(
=
(2)
=(![]() –4)·
–4)· =
(3)
→
=
(3)
→
![]() =
(
=
(![]() –4)·
(
–4)·
(![]() –1)·
–1)· =
(4)
=(
=
(4)
=(![]() –4)·
(
–4)·
(![]() –1)·
–1)· =
(5)
→
=
(5)
→
![]() =
(
=
(![]() –4)·
(
–4)·
(![]() –1)·
–1)·![]() =
(6)
=(
=
(6)
=(![]() –4)·(
–4)·(![]() –1)·
–1)·![]() =
(7)
→
=
(7)
→
Выполнены
операции:
(1):
выносим (–1) из первого столбца. (2):
[R1]+[R3]·2–[R2].
(3):
выносим (![]() –1)
из первой строки. (4):
[R3]–[R1]·3;
(5):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель. (7):
до вычисления
–1)
из первой строки. (4):
[R3]–[R1]·3;
(5):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель. (7):
до вычисления ![]() раскрывать скобки нецелесообразно.
раскрывать скобки нецелесообразно.
![]() =
(1)
=
=
(1)
= =(2)
=(
=(2)
=(![]() –1)·
–1)·
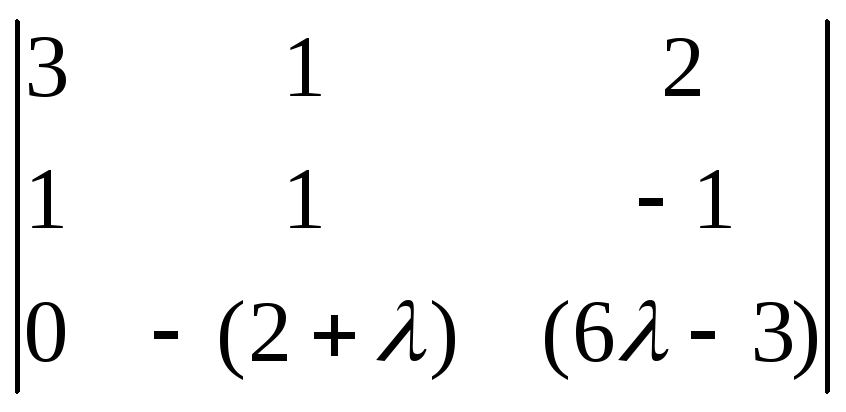 =
(3) →
=
(3) →
![]() =
(
=
(![]() –1)·
–1)·
 =(4)
=(
=(4)
=(![]() –1)·
–1)·![]() =
(
=
(![]() –1)·
(–7
–1)·
(–7![]() +16)
.
+16)
.
Выполнены
операции:
(1):
выносим (–1) из первого столбца;
[R2]+[R1]·2–[R3].
(2):
выносим (![]() –1)
из второй строки. (3):
[R1]–[R2]·3;
(4):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель.
–1)
из второй строки. (3):
[R1]–[R2]·3;
(4):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель.
Теперь
нетрудно получить: ![]() =(
=(![]() –1)·
–1)·![]() =
=
![]() ,
откуда следуют характеристические
корни:
,
откуда следуют характеристические
корни: ![]() =
=![]() =1,
=1,
![]() =
=![]() =2.
=2.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:
 (A)
(A)
3).
Для собственного значения ![]() =
1 система (A)
принимает вид:
=
1 система (A)
принимает вид:
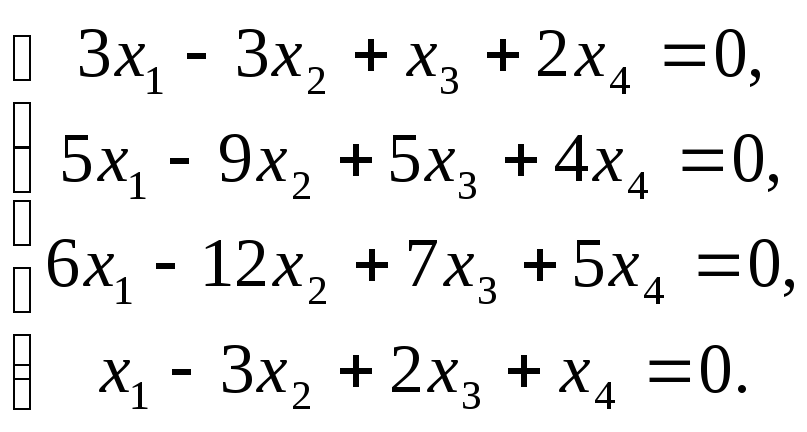 или
или
 (B)
(B)
Так
как определитель системы равен нулю,
то независимых уравнений не более трёх.
Ранг системы уравнений (B)
равен двум. Это значит, что ФСР этой
системы уравнений содержит два независимых
решения, то есть система (B)
даст нам два независимых собственных
вектора линейного преобразования:
![]() ,
,
![]() .
.
4).
Для собственного значения ![]() =
2 система (A)
принимает вид:
=
2 система (A)
принимает вид:
 (C)
(C)
Ранг
системы уравнений (C)
равен трём. Это значит, что ФСР этой
системы уравнений содержит одно
независимое решения, то есть система
(С) даст нам один собственный вектор
линейного преобразования: ![]() .
.
5).
В соответствии с теоремой 10.4 совокупность
векторов ![]() ,
,
![]() ,
,
![]() независима, но её недостаточно, чтобы
построить базу линейного пространства
независима, но её недостаточно, чтобы
построить базу линейного пространства
![]() .
Это значит: матрица заданного линейного
преобразования к диагональному виду
не приводится.
.
Это значит: матрица заданного линейного
преобразования к диагональному виду
не приводится.
Ответ: матрица к диагональному виду не приводится.
☻
Вопросы для самопроверки:
Что такое линейное преобразование пространства?
Как определяется матрица линейного оператора?
Как изменяется матрица линейного преобразования (оператора) при переходе от одного базиса к другому?
Что такое произведение линейных преобразований?
Что такое характеристическая матрица линейного преобразования?
Что такое характеристический многочлен линейного преобразования?
Что называется собственным вектором линейного преобразования, действующего в линейном пространстве R над числовым полем: K?
Что такое собственное значение линейного преобразования, действующего в линейном пространстве R над числовым полем: K?
Каким может быть максимальное число собственных значений у линейного оператора, действующего в линейном пространстве размерности n?
Зависят ли собственные значения линейного преобразования от выбора базиса в линейном пространстве, в котором действует это преобразование?
Всякий ли линейный оператор, действующий в линейном пространстве R над числовым полем K, имеет хотя бы одно собственное значение?
Как найти собственные значения линейного оператора?
Как найти собственные векторы линейного преобразования?
< * * * * * >
