239

ЛА: Глава 10

Глава 10. Линейные преобразования (операторы).

При рассмотрении - мерных векторных пространств мы использовали векторные выражения, в которых с векторами производилось некоторое воздействие:

▫ переход от системы векторов к системе векторов : =·, где - матрица перехода от базиса к базису ;

▫ преобразование строки координат b=(,,...,) вектора базе в строку координат b' =(,,...,) этого же вектора в базе : ·=, или в виде: =·.

Эти воздействия производятся на векторы пространства не явно, как бы косвенно. Например, координаты вектора изменились, потому что изменилась база пространства .

В настоящей главе рассмотрим такое преобразование линейного пространства, когда все векторы подвергаются одному и тому же преобразованию, причём так, что для любого вектора - мерного векторного пространства можно записать:

→ ;

→ ,

при этом , получаемый после преобразования вектор называется образом вектора , который называют прообразом. Для удобства записи вместо обозначения будем использовать , хотя первое было бы привычнее, по аналогии с обозначением функции в математическом анализе.

§ 1. Определение линейного преобразования.

Пусть имеем - мерное линейное векторное пространствои все его векторы подвергаются некоторому преобразованию. Мы будем рассматривать только линейные преобразования.

Определение: (10.1)

преобразование линейного векторного пространства называется линейным преобразованием этого пространства, если для любых векторов : 1) =, 2) =, для любого числа из некоторого поля.

Из определения следует: линейное преобразование переводит любую линейную комбинацию данных векторов в линейную комбинацию (с теми же коэффициентами) образов этих векторов:

(·+·+ …+·) = ·+·+…+·.

Рассмотрим основные свойства линейного преобразования линейного векторного пространства , вытекающие из определения линейного преобразования:

1⁰. Линейное преобразование оставляет неподвижным нулевой вектор: 0 = 0. Действительно, 0 =(0·)=0·= 0, по правилу умножения вектора на число.

2⁰. Образом вектора, противоположного заданному вектору , служит вектор, противоположный для образа этого вектора , то есть: =–. Достаточно учесть, что: –=(–1) и воспользоваться свойством 2) преобразования .

3⁰. Линейное преобразование , оставляющее неподвижным всякий вектор , а именно: = - называют тождественным.

4⁰. Линейное преобразование , отображающее всякий вектор , в нулевой вектор, а именно: =0 - называют нулевым.

Пусть в линейном векторном пространстве выделена база e=(e₁,e₂,…,e_n). Всякий вектор этого пространства можно представить в виде выражения: =(b₁,b₂,…,)·=·, где числа: b₁, b₂,…, - координаты вектора в базе . Заметим также, что в выражении: =· используется матрица-столбец базы .

Так как линейное преобразование , по определению, формирует вектор , принадлежащий исходному пространству , то его можно представить в базе e в виде:

=(,,...,)·=·. (1)

Для вычисления координат вектора-образа: воспользуемся определением и свойствами линейного преобразования :

====· (2)

5⁰. Выражение (2) является обобщением (доказанным!) требования: =, где , используемое в требовании, всего лишь число. Теперь мы видим, что перестановочны также символы и - строка координат вектора в базе : =·, где вектор есть матрица-столбец.

Так как , - векторы пространства , то каждый из них можно записать координатами в базе :

==·=·. (3)

Учитывая все полученные выражения, можно записать результат применения линейного преобразования к вектору :

= =·=·· → =·. (4)

Замечание: рассмотрен вариант решения задачи для случая, когда система векторов базыизображается в виде матрицы-столбца. Аналогично задача решается для базы, изображаемой в виде матрицы-строки.

Говорят, что матрица задает линейное преобразование! В таком случае в векторном пространстве установлено взаимно однозначное соответствие между всеми квадратными матрицами порядка и линейными преобразованиями пространства! Выражение матрицы конкретного линейного преобразования зависит от выбора базы, в которой записывается матрица преобразования. Это следует из доказательства выражения (3). Далее эта зависимость будет определена.

Полезно рассмотреть простые примеры, иллюстрирующие применение линейного преобразования векторного пространства .

☺☺

Пример 10–01:Пусть на плоскости задана система координат и определено линейное пространство геометрических векторов. При неподвижной системе координат плоскость поворачивается относительно точкиOна угол . Является ли этот поворот линейным преобразованием в пространстве?

Решение:

1). Учитывая, что геометрические векторы свободные, будем считать, что вектор имеет начало в точкеO. Преобразование переводит вектор в вектор, принадлежащий.

2). Пусть заданы два произвольных вектора и, принадлежащие. В соответствии с определением операций суммы геометрических векторов и умножения вектора на число построим вектор: =+и вектор =·.

3). Вектор диагональ параллелограмма, построенного на векторах и. Преобразование есть поворот диагонали параллелограмма на уголотносительно точкиO.Преобразование, применённое к векторам и , поворачивает каждый из них на тот же угол . В таком случае требование =+выполняется.

4). Геометрически очевидно также, результат не зависит от того, что будет меняться порядок операций: сначала вектор умножить на число, потом повернуть получившийся вектор на угол , или наоборот. В таком случае требование= выполняется.

5). Заданное преобразование плоскости является линейным преобразованием пространства .

Ответ: является.

Пример 10–02: Показать, что умножение квадратных матриц 2-го порядка слева на данную матрицуявляется линейным преобразованием пространства всех матриц 2-го порядка.

Решение:

1). Запишем произвольный вектор пространства: == x₁+x₂+x₃+x₄, и определим преобразование : то есть произведение:=·.

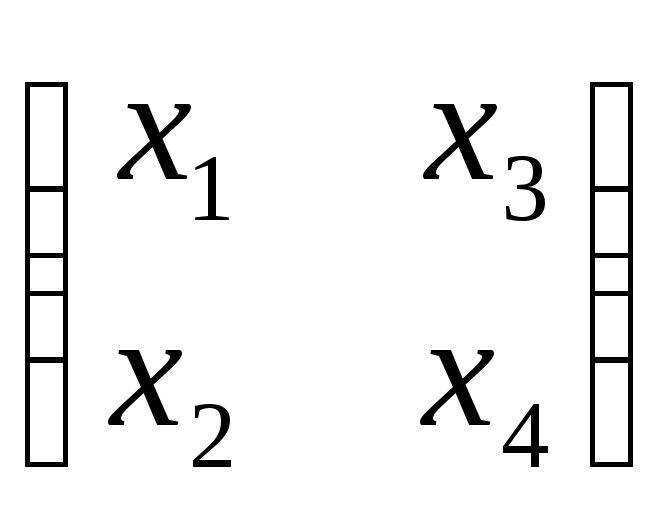2). Используя линейные свойства матриц, запишем: =·, и=·. Это значит, что требование линейного преобразования: = выполняется.

3). Пусть задан также вектор: =, и записано:=·.

4). Запишем сумму векторов: ==+и линейное преобразование суммы векторов:=·. Учитывая линейные свойства матриц, получаем: требование линейного преобразования:=также выполняется.

5). Вывод: заданное преобразование - линейное.

Ответ: является линейным преобразованием.

Пример 10–03: Пусть задан вектор=(x₁,x₂,x₃) линейного пространства. Записано преобразование пространства:=(x₂+x₃,2x₁+x₃,3x₁–x₂+x₃). Выяснить, является ли оно линейным. Если преобразование линейное, найти его матрицу в том же базисе, в котором заданы векторыи.

Решение:

1). Запишем базис пространства: =(1,0,0), =(0,1,0),=(0,0,1). Это значит, что произвольный вектор линейного пространства может быть записан в виде:=x₁+x₂+x₃.

2). Пусть заданы два произвольных вектора и , принадлежащие . В соответствии с определением операций суммы векторов:=+=(x₁+y₁,x₂+y₂,x₃+y₃) и=(x₁,x₂,x₃).

3). Запишем векторы-образы для векторов, участвующих в доказательстве линейности :

= (+y₃, 2+y₃, 3y₁–+y₃) и =(x₂+x₃,2x₁+x₃,3x₁–x₂+x₃);

== (+x₃++y₃, 2+x₃+2+y₃, 3x₁–++3y₁–+y₃).

4). Из представленных записей следует: требование =выполняется, требование= выполняется → преобразование - линейное.

5). Матрицу линейного преобразования легко получаем (видим!), если изобразить шаблон выражения =·:

= (x₂+x₃,2x₁+x₃,3x₁–x₂+x₃)= (x₁,x₂,x₃) ·.

Ответ: является линейным преобразованием с матрицей:.

Пример 10–04: Пусть задан вектор=(x₁,x₂,x₃) линейного пространства. Записано преобразование пространства:=(x₁–x₂+x₃, x₃, x₂). Выяснить, является ли оно линейным. Если преобразование линейное, найти его матрицу в том же базисе, в котором заданы векторыи.

Решение:

1). Запишем базис пространства: =(1,0,0), =(0,1,0),=(0,0,1). Это значит, что произвольный вектор линейного пространства может быть записан в виде:=x₁+x₂+x₃.

2). Пусть заданы два произвольных вектора и , принадлежащие . В соответствии с определением операций суммы векторов:=+=(x₁+y₁,x₂+y₂,x₃+y₃) и=(x₁,x₂,x₃).

3). Запишем векторы-образы для векторов, участвующих в доказательстве линейности :

= (y₁–y₂+y₃, y₃, y₂) и =((x₁–x₂+x₃), x₃, x₂);

== (+y₁–(+y₂)++y₃, +y₃, +y₂).

4). Из представленных записей следует: требование = выполняется, требование= выполняется → преобразование - линейное.

5). Матрицу линейного преобразования легко получаем (видим!), если изобразить шаблон выражения =·:

= (x₁–x₂+x₃, x₃, x₂)= (x₁,x₂,x₃) ·.

Ответ: является линейным преобразованием с матрицей:.

Пример 10–05: Показать, что дифференцирование является линейным преобразованием пространства всех многочленом степени от одного неизвестного с вещественными коэффициентами. Найти матрицу этого преобразования в базе:

а) 1, x;x²; ... , ;

б) 1, x-c; ; ... , гдеc - вещественное число.

Решение:

Общая часть для обоих заданий:

1). Запишем в базе а)многочлен:=, его координаты – коэффициенты при переменной. Аналогично=.Сумма многочленов:k=+=; произведение многочлена на вещественное число:= .

2). Обозначим: -оператор дифференцирования. Используя теоремы математического анализа, замечаем, что оператор является линейным по отношению к векторам-многочленам, записанным в базе а).

3). Пусть многочлен записан в виде: =, его координаты в базе б) – вещественные числа. Вопрос о линейностине вызывает затруднений.

Задание а): используем базу а).

4). Запишем производную для многочлена: =по независимой переменнойx, используя правила дифференцирования:

== ,

координаты в базе а) вектора :m'=(,, ..., , 0).

5). Матрицу линейного преобразования легко получаем (видим!), если изобразить шаблон выражения =·:

=(,, ..., , 0)= () ·.

Задание б): используем базу б).

6). Запишем производную для многочлена: =по независимой переменнойx, используя правила дифференцирования:

== ,

координаты в базе а) вектора :m'=(,, ..., , 0).

7). Матрицу линейного преобразования легко получаем (видим!), если изобразить шаблон выражения =·:

=(,, ..., , 0)= () ·.

Ответ:- линейное преобразование как для базы, заданной в записи а), так и в записи б) с матрицей: для случая а):C₁. для случая б):C₂.

Пример 10–06: Пусть совокупность векторов:e=(,,) есть база трехмерного линейного пространства. В этой базе задан вектор =(5+–2)=(5,1,-2). Пустьлинейное преобразование задается матрицей:=в базе , которая используется в виде матрицы-столбца. Найти образ .

Решение:

1). Воспользуемся формулой (4) для вектора : ==·.

2). В нашем случае получаем: = (5,1,–2) ·=(–9, 4, –6).

Ответ: =(–9, 4, –6).

☻