ШУМ И ЕГО АНАЛИЗ

В электронных схемах во всех компонентах напряжение и ток всегда сопровождаются шумовыми напряжением и током, которые называют просто шумом. Общим признаком всех шумов (не путать с квазишумовыми сигналами) является, во-первых, невозможность предсказания появления какой-либо конкретной его величины в конкретный момент времени, т.е. егослучайностьи, во-вторых,равенство нулю его средней величины.

Основные определения

Несмотря на равенство нулю средней величины шума, физически он существует, и квадратвеличины шума не равен нулю. Определяютсреднеквадратичную величину (MeanRootSquare) шума (Noise):

- для шумового напряжения (4.1)

- для шумового тока (4.2)

здесь Т – интервал времени усреднения. Чем больше интервал времени Т, тем точнее величины и. Очевидно, что квадраты величин в (4.1) и (4.2) естьмощность, рассеиваемая в резисторе 1 Ом, если к нему приложены среднеквадратичное напряжениеили постоянное, численно равное ему, а также если через резистор 1 Ом течет среднеквадратичный токили постоянный, численно равный ему.

Отношение сигнала к шуму (SignaltoNoiseRatio) определяется так:

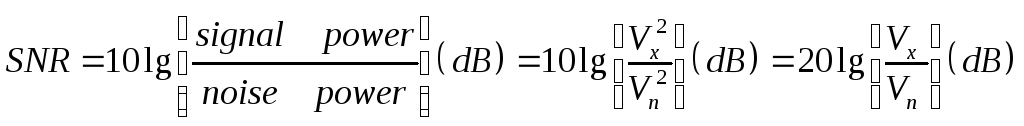. (4.3)

Здесь - мощность сигнала,- мощность шума.

Хотя децибелы (дБ)по определению относятся котношению двух величин, оказалось полезным введение определение величины мощности вдБдляабсолютных значений сигнала. Условно принято, что мощность, равная 1 мВт называется 1дБм (1dBm). Например, мощность в 1 мкВт обозначается как – 30 (дВм). В случае обозначения в (дВм)напряжений, определяют 1 дБм (dBm) как напряжения (среднеквадратичные или постоянные) на ряде резисторов (600 Ом, 75 Ом и 50 Ом), при которых рассеиваются одинаковые мощности в 1 мВт.

Cуммирование шумов

Рассмотрим случай соединенных последовательно источников шумового напряжения и соединенных параллельно источников шумового тока (Рис. 4.1).

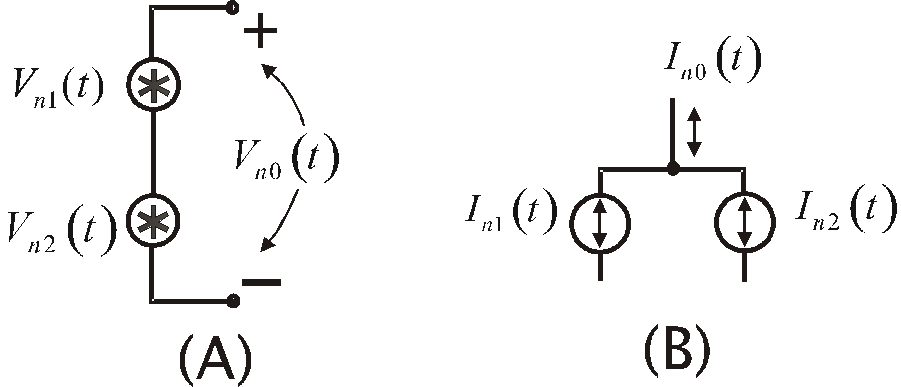
Рис.4.1. Комбинирование двух шумовых источников:

(а) напряжения и (в) тока.

Определим как(4.4)

Тогда

(4.5)

Первые два члена в правой части (4.5) – мощности шумов обоих источников. Последний член выражает корреляцию между источниками шума. Принято определять корреляцию С следующим образом:

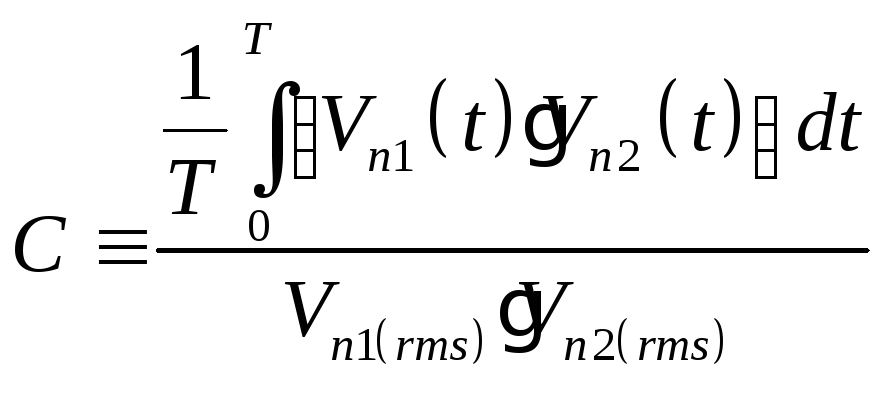(4.6)

С учетом этого определения (4.5) можно записать:

(4.7)

Коэффициент корреляции С удовлетворяет неравенству . Если, то два сигнала полностью коррелированы, если же, то сигналы некоррелированы. Промежуточные значения С означают частичную корреляцию. Итак, в случае двух некоррелированных сигналов

, (4.8)

в случае же полностью коррелированных сигналов (например, двух синусоидальных сигналов с одинаковыми частотами и с фазами 0 или 180 градусов)

(4.9)

В усилительных электронных схемах конкретная величина шума в большинстве случаев много меньше установленных или ожидаемых величин тока или напряжения, поэтому можно считать, что шумовые напряжения и токи не влияют на характеристики компонентов, зависящие от тока и/или напряжения (например, крутизна транзистора), и шумовые напряжения двух последовательно включенных приборов (или шумовые токи двух параллельно включенных приборов ) взаимно не коррелируют.

Анализ шума в частотной области

Ввиду случайности и непредсказуемости значений шумового сигнала, его мощность (или) непрерывно распределена в частотной области. Ввидунепрерывного распределения, в бесконечно малой полосе частот мощность шума равнанулю!Когда говорят о конкретной спектральной плотности шума на какой – то частоте, то по умолчанию имеют в виду мощность шума в частотной полосе 1 Гц, и упомянутая частота находится в середине этой полосы. Полная мощность шума получается интегрированием плотности шума по всему спектру частот:

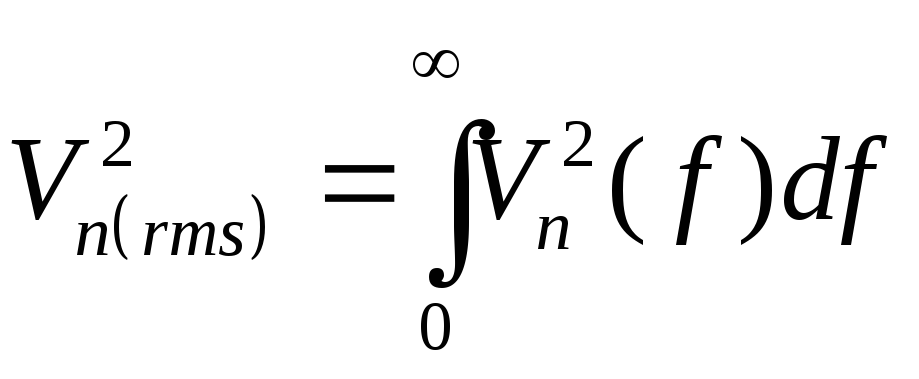(4.10)

Рассмотрим прохождение шумового сигнала через фильтр с передаточной функцией. Спектральная плотностьмощности шума равна:

(4.11)

Полная мощность шума равна

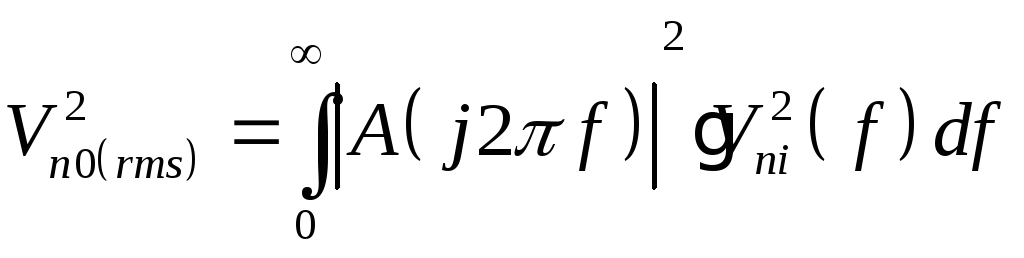(4.12)

Среднеквадратичное значение плотности шума равно

(4.13)

Поскольку среднеквадратичное значение шума определяется обычным для линейного фильтра образом, посредством модуля передаточной функции, а не через ее квадрат, удобнее пользоваться среднеквадратичным значением, а не мощностью шума.

Предположим теперь, что шум системы является суммойшумовых сигналов, и каждый шумовой сигналпроходит через фильтр. Тогда

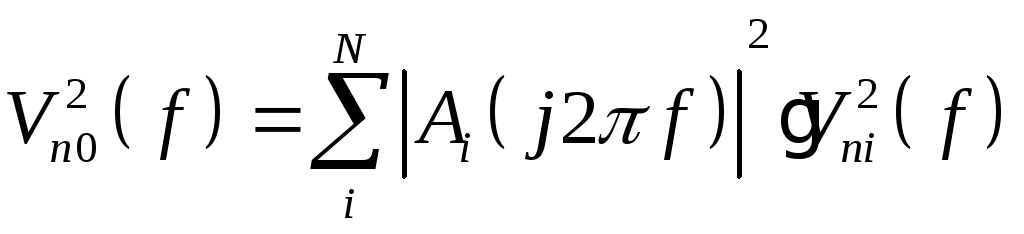(4.14)

Если шумовые сигналы взаимно не коррелированы, то на выходе фильтров они также не коррелированы.