
1 семестр_1 / ЛА / Модуль 1 / МП12_Николаев_Олег_lab01
.docxОтчет к упражнению 1:
1) ввести (x+1)*(x-1)
Получил сообщение:
>> (x+1)*(x-1)
??? Undefined function or variable 'x'.
2) ввести:
>> syms x
>> f=(x+1)*(x-1)
>> collect(f)
Получил сообщение:
>> syms x
>> f=(x+1)*(x-1)
f =
(x+1)*(x-1)
>> collect(f)
ans =
-1+x^2
Ввести >> f=collect(f)
Получил сообщение:
>> f=collect(f)
f =
-1+x^2
Вывод: команда collect упростила выражение f (раскрыла скобки).
3) присвоить x какое-нибудь число:
>> x=2
x =
2
4) снова вызвать f:
>> f
f =
-1+x^2
5) снова вызвать f=(x+1)*(x-1):
>> f=(x+1)*(x-1)
f =
3
Вывод: в f присвоилось значение выражения (2+1)*(2-1)
Отчет к упражнению 2: Работа с массивами.
1) создадим матрицу B размером 1x2:
>> B=[1 2;3 4]
B =
1 2
3 4
2) вызовем элементы В(2) и В(1,2):
>> B(2)
ans =
3
>> B(1,2)
ans =
2
Отчет к упражнению 3:
1) вектор-строку a вектора а={1,2,3,4,5} с помощью
a) ввода чисел c пробелами:
>> a=[1 2 3 4 5]
a =
1 2 3 4 5
b) ввода чисел с запятыми;
>> a=[1,2,3,4,5]
a =
1 2 3 4 5
c) стандартной функцией horzcat()
>> a=horzcat(1,2,3,4,5)
a =
1 2 3 4 5
d) двоеточия «:» с шагом можно задать те же числа от 1 до 6 с шагом 1
>> a=1:1:6
a =
1 2 3 4 5 6
2)Задать вектор-столбец b ={1, 1.9, 2.8, 3.7}
a) с помощью точки запятой «;» ;
>> b=[1;1.9;2.8;3.7]
b =
1.0000
1.9000
2.8000
3.7000
b) транспонировав вектор-строку a, с помощью символа «'» - одинарная кавычка (буква э в латинском регистре)
>> a=[1,1.9,2.8,3.7];b=a'
b =
1.0000
1.9000
2.8000
3.7000
с) проделайте то же действие с вектором b
>> b=b'
b =
1.0000 1.9000 2.8000 3.7000
d) задайте вектор b стандартной функцией vertcat()
>> b=vertcat(1,1.9,2.8,3.7)
b =
1.0000
1.9000
2.8000
3.7000
e) с помощью двоеточия с шагом и транспонирования
>> b=1:0.9:3.7
b =
1.0000 1.9000 2.8000 3.7000
>> b=b'
b =
1.0000
1.9000
2.8000
3.7000
Отчет к упражнению 4:
1) Построить последовательно три прямые
(0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0) .
>> grid on
>> line([0,2],[0,1])

>> line([0,-2],[0,-1])

>> line([-2,0],[4,0])

Отчет к упражнению 5:
1) Построить последовательно
прямые (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
>> grid on
>>line([0,2],[0,1])
>> line([0,2],[2,0])

>> line([0,3],[2,0])

Отчет к упражнению 6:
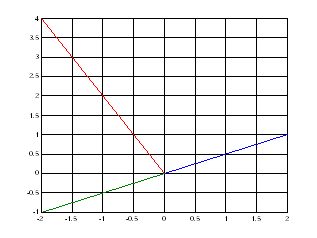
1) И теперь построим сразу все три прямые прямые
(0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0) .
>> grid on;line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])
Отчет к упражнению 7:
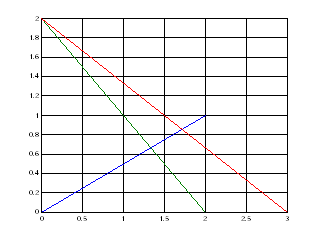
1) Постройте три прямые (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) с помощью одной команды line.
>> grid on;line([0,0,0;2,2,3],[0,2,2;1,0,0])
Отчет к упражнению 8:
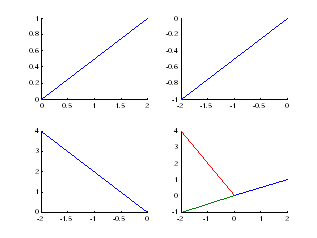
1) Создать графическое окно для четырех координатных плоскостей. В первых трех построить по одной прямой, в четвертой все три прямые.
Прямые (0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0)
>> subplot(2,2,1)

>> line([0;2],[0;1])

>> subplot(2,2,2)

>> line([0;-2],[0;-1])

>> subplot(2,2,3)
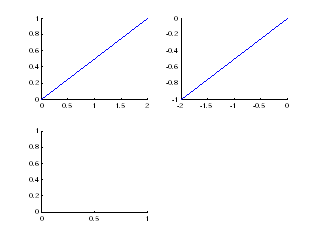
>> line([-2;0],[4;0])

>> subplot(2,2,4)
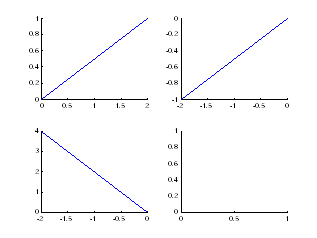
>> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])
Отчет к упражнению 9:
1) Создать графическое окно для четырех координатных плоскостей. В третьей области построить все три прямые, в остальных по одной.
Прямые:
(0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
>> subplot(2,2,1)
>> line([0;2],[0;1])

>> subplot(2,2,2)
>> line([0;2],[2;0])

>> subplot(2,2,3)
>> line([0,0,0;2,2,3],[0,2,2;1,0,0])

>> subplot(2,2,4)
>> line([0;3],[2;0])

Отчет к упражнению 10:
1) Построить векторы для прямых (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
>> grid on;hold on
>> line([0,0,0;2,2,3],[0,2,2;1,0,0])
>> plot(2,1,'>b','lineWidth',4)
>> plot(2,0,'vg','lineWidth',4)
>> plot(3,0,'>r','lineWidth',4)

