
- •Глава 4. Уравнения в полных дифференциалах.
- •§ 1. Определение дифференциального уравнения в полных дифференциалах.
- •§ 2. Способ решения ду в полных дифференциалах и общий алгоритм решения.
- •§ 3. Интегрирующий множитель.
- •§ 4. Применение уравнений в полных дифференциалах: задачи из геометрии.
- •§ 5. Применение уравнений в полных дифференциалах: задачи из физики.
§ 4. Применение уравнений в полных дифференциалах: задачи из геометрии.
Настоящий параграф продолжает тему построения кривых линий заданием некоторых дифференциальных свойств этих кривых. В Главе 1, в § 3 настоящего Пособия получены выражения для характерных отрезков кривой, связанных с касательной и нормалью этой кривой в каждой её точке.
Ниже представлены примеры, в которых дифференциальные свойства кривых линий изучаются с использованием дифференциальных уравнений в полных дифференциалах.
☺☺
Пример 4–07:
Найти
уравнение кривой, проходящей через
точку
(1,0) и обладающей свойством: длина отрезка
![]() ,
отсекаемого на оси
,
отсекаемого на оси
![]() касательной к кривой в точке
касательной к кривой в точке
![]() ,
больше модуля
,
больше модуля
![]() .
.
В Главе
1, в § 3 настоящего Пособия получено
выражение:
для отрезка
![]() =
=![]() ,
отсекаемого касательной на оси ординат.
,
отсекаемого касательной на оси ординат.
Р ешение:
ешение:
1). Из
условия задачи следуют два варианта
использования равенства
![]() =
=![]() :
:
▪ Случай-1:
![]() =
=![]() , (1)
, (1)
▪ Случай-2:
![]() =
=![]() , (2)
, (2)
или
▪ Случай-1:
![]() =0, (1)
=0, (1)
▪ Случай-2:
![]() =0. (2)
=0. (2)
Случай-1.
2).
Проверим выполнение условия
![]() =
=![]() .
Вычислим:
.
Вычислим:
![]() =1,
=1,
![]() =1
→ уравнение (1) есть уравнение в полных
дифференциалах. Далее применяем
стандартный алгоритм решения уравнения
в полных дифференциалах.
=1
→ уравнение (1) есть уравнение в полных
дифференциалах. Далее применяем
стандартный алгоритм решения уравнения
в полных дифференциалах.
2).
Вычисляем:
![]() =
=![]() +
+![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() +
+![]() ,
или (учитывая при интегрировании
переменную
,
или (учитывая при интегрировании
переменную
![]() как параметр)
как параметр)
![]() =
=![]() +
+![]() .
.
где
слагаемое
![]() играет роль постоянной интегрирования,
то есть отражает множество первообразных.
играет роль постоянной интегрирования,
то есть отражает множество первообразных.
3). Так
как
![]() =
=![]() ,
вычисляем:
,
вычисляем:
![]() =
=![]() –
–![]()
![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() –
–![]()
![]() =0.
=0.
4). Имея
функцию
![]() ,
запишем выражение для вычисления функции
,
запишем выражение для вычисления функции
![]() =
=![]() .
В нашем случае:
.
В нашем случае:
![]() =0.
=0.
5). Запишем
общее решение заданного уравнения в
виде:
![]() =
=![]() =
=![]() .
.
6).
Учитывая начальные условия, получим:
![]() .
Запишем частное решение заданного
уравнения в виде:
.
Запишем частное решение заданного
уравнения в виде:
![]() =
=![]() .
.
Ответ:
общее решение
![]() =
=![]() ,
частное решение:
,
частное решение:
![]() =
=![]() .
.
Случай-2.
2).
Проверим выполнение условия
![]() =
=![]() .
Вычислим:
.
Вычислим:
![]() =3,
=3,
![]() =1
→ уравнение (1) не есть уравнение в полных
дифференциалах. Запишем уравнение (2) в
виде:
=1
→ уравнение (1) не есть уравнение в полных
дифференциалах. Запишем уравнение (2) в
виде:
![]() –
стандартная
форма линейного уравнения, где
–
стандартная
форма линейного уравнения, где
![]() и
и ![]() .
Далее применяем стандартный алгоритм
решения линейного уравнения, принимая:
.
Далее применяем стандартный алгоритм
решения линейного уравнения, принимая:
![]() .
.
3). Вычисляем
интеграл:
![]() =
=![]() =
=![]() .
Тогда:
.
Тогда:![]() =
=![]() =
=![]() .
.
4). Вычисляем
интеграл:
![]() =
=![]() =
=![]() +
+![]() =
=![]() +
+![]() .
.
5). Запишем общее
решение уравнения:
![]() =
=![]() =
=![]() ∙
∙![]() =
=![]() .
.
6). Через точку
(1,0) проходит интегральная кривая:
![]() =
=![]() ,
так как
,
так как![]() =
=![]() .
.
Ответ:
для случая-1: общее решение
![]() =
=![]() ,
частное решение
,
частное решение
![]() =
=![]() ;
;
для
случая-2: общее решение ![]() =
=![]() ,
частное решение:
,
частное решение: ![]() =
=![]() .
.
Замечание: Пример интересен тем, что для решения геометрической задачи потребовалось решать два разных типа дифференциальных уравнений, хотя дифференциальные свойства кривой определены вполне однотипными условиями!..
§ 5. Применение уравнений в полных дифференциалах: задачи из физики.
Рассмотрим еще один пример применения дифференциальных уравнений в задачах физики. Важно, что само уравнение естественно следует из наблюдаемого физического явления!
☺☺
Пример 4–08:
Движение тела под действием постоянной
силы в случае, если сопротивление среды
пропорционально скорости, определяется
ДУ:
![]() .
Найти общее решение этого уравнения.
.
Найти общее решение этого уравнения.
Решение:
1).
Прежде всего, отметим, что исходное
уравнение не имеет очевидных решений,
Обозначив величины:
![]() =
=![]() и
и
![]() =
=![]() ,
перепишем уравнение в виде:
,
перепишем уравнение в виде:
![]() .
Решение этого уравнения зависит от
того, к какому из способов мы обратимся.
.
Решение этого уравнения зависит от
того, к какому из способов мы обратимся.
Способ-1.
2).
Пусть уравнение, записанное в виде:
![]() ,
было классифицировано
нами как линейное дифференциальное
уравнение, где
,
было классифицировано
нами как линейное дифференциальное
уравнение, где
![]() и
и
![]() .
Принимая
.
Принимая
![]() ,
воспользуемся стандартным алгоритмом
линейного уравнения.
,
воспользуемся стандартным алгоритмом
линейного уравнения.
3). Вычисляем
интеграл:
![]() =
=![]() =
=![]() .
Тогда:
.
Тогда:![]() =
=![]() =
=![]() .
.
4). Вычисляем
интеграл:
![]() =
=![]() =
=![]() +
+![]() =
=![]() +
+![]() .
.
5). Запишем общее
решение уравнения:
![]() =
=![]() ∙
∙![]() =
=![]() .
.
Ответ:
![]() =
=![]() –
общее решение.
–
общее решение.
Способ-2.
Замечание: Конечно, мы видим, что задано линейное уравнение (даже в стандартной форме!), и его можно решить, применив стандартный алгоритм... Пусть мы этого не заметили!..
2).
Применим к уравнению:
![]() интегрирующий множитель:
интегрирующий множитель:
![]() =
=![]() =
=![]() .
В таком случае, исходное уравнение
принимает вид:
.
В таком случае, исходное уравнение
принимает вид:
![]() .
Далее возможны разные способы решения
полученного уравнения.
.
Далее возможны разные способы решения
полученного уравнения.
Способ-2-1.
5). Мы
могли заметить, что полученное уравнение
можно записать (применяя дифференциал
функции двух переменных) в виде равенства:
![]() ,
которое сразу (!) интегрируется:
,
которое сразу (!) интегрируется:
![]() =
=![]() .
Результат интегрирования:
.
Результат интегрирования:
![]() =
=![]() +
+![]() ,
или
,
или
![]() =
=![]() .
.
Способ-2-2.
5). Мы не
заметили, что запись уравнения
![]() допускает применение Способа-2-1. Перепишем
это уравнение:
допускает применение Способа-2-1. Перепишем
это уравнение:
![]() – стандартная запись уравнения в полных
дифференциалах.
Легко убедиться, что после применения
стандартного алгоритма решения уравнения
в полных дифференциалах решение будет
иметь вид:
– стандартная запись уравнения в полных
дифференциалах.
Легко убедиться, что после применения
стандартного алгоритма решения уравнения
в полных дифференциалах решение будет
иметь вид:
![]() =
=![]() .
.
Ответ:
общее решение:
![]() =
=![]() .
.
Замечание: Пример иллюстрирует сразу 3 способа решения одной и той же задачи. Нетрудно заметить также, что способы решения задачи, то есть получение общего решения задачи, различаются как по сложности, так и по трудоёмкости!..
Пример 4–09:
Скорость охлаждения тела пропорциональна
разности температур тела и окружающей
среды (закон Ньютона). Найти зависимость
температуры
![]() от времени
от времени
![]() ,
если тело, нагретое до
,
если тело, нагретое до
![]() градусов, внесено в помещение, температура
которого постоянна и равна
градусов, внесено в помещение, температура
которого постоянна и равна
![]() градусам.
градусам.
Р ешение:
ешение:
Замечание: рисунок мотивирует решение задачи, а также намекает, что охлаждение тела происходит за счет молекулярного взаимодействия тела и среды: тело подвешено к потолку на тонкой нити, обладающей минимальной теплопроводностью.
1). Из условия задачи следует дифференциальное уравнение:
![]() =
=![]() . (1)
. (1)
2). Уравнение (1) – ДУ с разделяющимися переменными. Его стандартная форма записи:
![]() =
=![]() . (2)
. (2)
3). В результате интегрирования уравнения (2) получаем общее решение задачи:
![]() =
=![]() . (3)
. (3)
4). Учитывая начальные условия, получаем частное решение задачи:
![]() =
=![]() . (4)
. (4)
Ответ:
общее решение:
![]() =
=![]() ,
частное решение:
,
частное решение:
![]() =
=![]() .
.
Замечание: 1). Полученный результат может рассматриваться как общая технология, которая будет применяться для расчетов аналогичных процессов для разных тел и разных начальных условий.
2).
Характеристикой конкретного тела
является коэффициент пропорциональности
![]() ,
который определяют экспериментально!
,
который определяют экспериментально!
3). Учитывая широкие возможности использования интегрирующего множителя, рассматриваемая задача тоже может быть отнесена к теме ДУ в полных дифференциалах!
Пример 4–10:
Через сколько времени температура тела
понизится от величины
![]() до величины
до величины
![]() в помещении, температура которого равна
в помещении, температура которого равна
![]() .
Известно, что за первые 10 мин тело
охладилось до температуры
.
Известно, что за первые 10 мин тело
охладилось до температуры
![]() ?
?
Решение:
Замечание: задача
интересна как приложение уже полученного
в Примере 4-09 общего решения:
![]() –
закон охлаждение тела в заданных
условиях. В рассматриваемом Примере
определены начальные условия охлаждения
тела: начальная температура тела
–
закон охлаждение тела в заданных
условиях. В рассматриваемом Примере
определены начальные условия охлаждения
тела: начальная температура тела
![]() ,
температура помещения
,
температура помещения
![]() .
.
1).
Из
условия задачи следует:
![]() ,
,
![]() –
понижение температуры в
процессе, который длился
–
понижение температуры в
процессе, который длился
![]() =10
мин.
=10
мин.
2).
Из
уравнения:
![]() для названных исходных данных
для названных исходных данных
![]() →
→![]() =
=![]() .
.
3).
Из
уравнения
![]() запишем
запишем
![]() =
=![]() ,
или
,
или
![]() =
=![]() для названных исходных данных.
В результате вычисления получаем:
для названных исходных данных.
В результате вычисления получаем:
![]() ≈40
мин.
≈40
мин.
Ответ:
температура понизится за время
![]() ≈ 40
мин.
≈ 40
мин.
☻
Вопросы для самопроверки:
Задана функция:
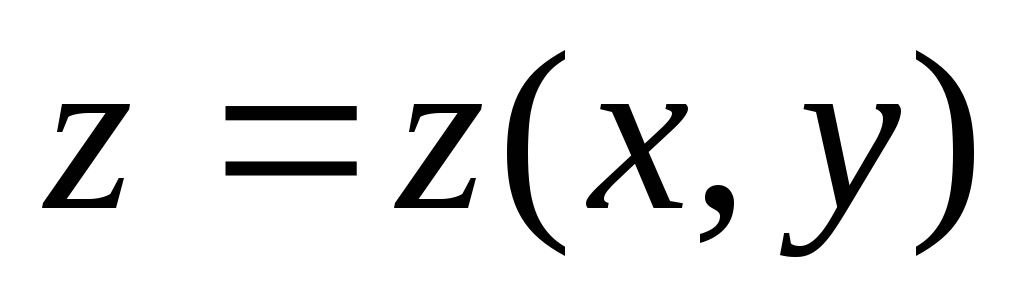 .
Записать выражение для полного
дифференциала этой функции.
.
Записать выражение для полного
дифференциала этой функции.Задана функция:
 .
Записать выражение для частной
производной
.
Записать выражение для частной
производной
 .
.Задана функция:
 .
Записать выражение для частной
производной
.
Записать выражение для частной
производной
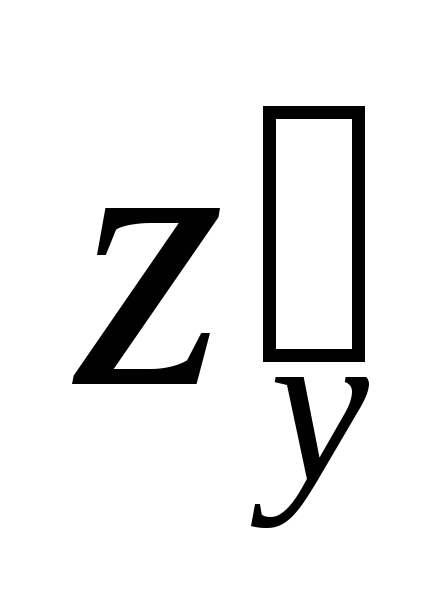 .
.Имеем дифференциальное уравнение:
 .
Как проверить, является ли это уравнение
уравнением в полных дифференциалах?
.
Как проверить, является ли это уравнение
уравнением в полных дифференциалах?Каков стандартный алгоритм решения ДУ в полных дифференциалах?
Как применяют стандартный алгоритм решения ДУ в полных дифференциалах?
Что такое интегрирующий множитель дифференциального уравнения?
При каком условии интегрирующий множитель ДУ зависит только от переменной
 ?
?При каком условии интегрирующий множитель ДУ зависит только от переменной
 ?
?
• ◄ ≡ ► •
