
- •Министерство общего и профессионального
- •Критерий Михайлова
- •Критерий Найквиста
- •Это значит, что годограф не должен охватывать начало координат (рис. 3).
- •Система с неустойчивой разомкнутой цепью
- •В первом случае штриховка справа, во втором – справа. Кроме этой гиперболы получаем две особые прямые (для детального анализа графика можно обратиться к рисунку 9)
- •Контрольные вопросы
- •Учебное издание
Критерий Найквиста
Частотный критерий устойчивости (критерий Найквиста) базируется на частотных характеристиках разомкнутой цепи системы автоматического управления и дает правила, согласно которым по виду частотной характеристике разомкнутой цепи можно судить об устойчивости замкнутой системы.
Рассмотрим разные случаи:
Система устойчива в разомкнутом состоянии.
Передаточная функция разомкнутой цепи:
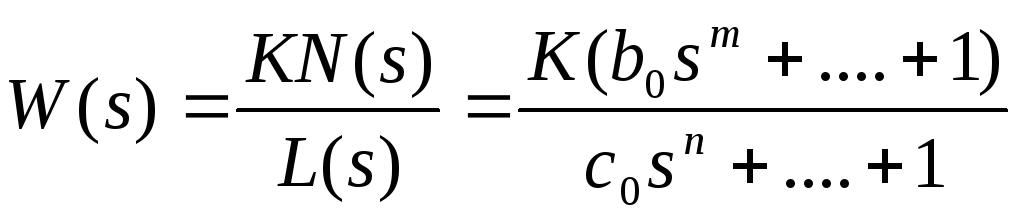 ,
m<n
(5)
,
m<n
(5)
Этот случай соответствует системам автоматического управления без астатизма. Введем вспомогательную функцию
![]()
где D(s) – характеристический многочлен замкнутой системы, а L(s) – характеристический многочлен разомкнутой цепи этой системы.
Подставим s = jw, и получим
![]()
По
критерию Михайлова изменение аргумента
L(jw)
при
![]() равно
равно![]()
так как предполагается, что разомкнутая
цепь устойчива. С другой стороны,
требуется, чтобы система была устойчива
в замкнутом состоянии. Для этого нужно
потребовать, чтобы изменения аргумента
D(jw)
при
так как предполагается, что разомкнутая
цепь устойчива. С другой стороны,
требуется, чтобы система была устойчива
в замкнутом состоянии. Для этого нужно
потребовать, чтобы изменения аргумента
D(jw)
при
![]() также
равнялось
также
равнялось![]() .
.
Отсюда
следует, что изменение аргумента
![]() должно быть:
должно быть:
![]()
Это значит, что годограф не должен охватывать начало координат (рис. 3).
Формулировка частотного критерия Найквиста: Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1) (рис.4).
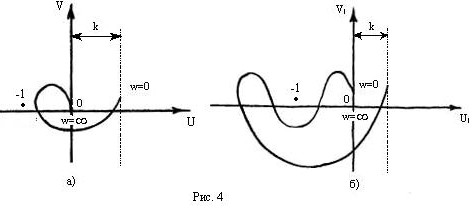
Первый график рис.4 соответствует случаю, когда устойчивость системы нарушается только с увеличением общего коэффициента усиления разомкнутой цепи К, а второй график случаю, когда и при уменьшении К система может стать неустойчивой.
Неустойчивость замкнутой системы иллюстрируется на рис.5.
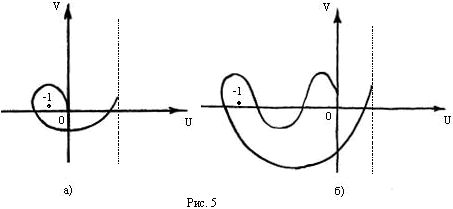
Система, нейтральная в разомкнутом состоянии
Характеристический многочлен разомкнутой цепи L(s) имеет ненулевые корни, а остальные все корни имеют отрицательные вещественные части.
Передаточная функция разомкнутой цепи W(s) имеет соответственно нулевые полюса:
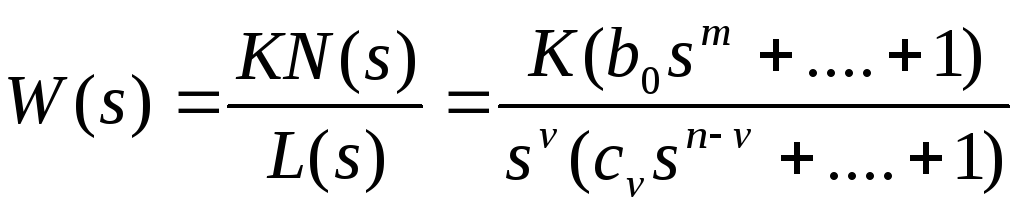 ,
m<n
,
m<n
Это соответствует астатическим системам, причем - порядок астатизма.
Рассмотрим случай = 1, т.е.
![]()
При = 1,2,3 получаем ту же формулировку критерия – неохват точки (-1), как показано на рис.6.

Система с неустойчивой разомкнутой цепью
Пусть характеристический многочлен L(s) разомкнутой цепи имеет l корней с положительной вещественной частью. Тогда введенная выше вспомогательная функция
![]()
при
замене s=jw,
согласно критерию Михайлова для
устойчивости замкнутая система, должна
иметь следующее изменение аргумента
при
![]() :
:
![]()
Это значит, что для устойчивости замкнутой системы требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи охватывала точку (-1) против часовой стрелки на угол 1, гдеl– число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи данной системы. Другими словами, левее точки (-1) разность между числом положительных и числом отрицательных переходов амплитудно-фазовой частотной характеристики через ось абсцисс должно равнятьсяl/2.
Формулу
![]() можно использовать
для подсчета числа корней m,
лежащих справа, когда система неустойчива,
а именно
можно использовать
для подсчета числа корней m,
лежащих справа, когда система неустойчива,
а именно
![]()
П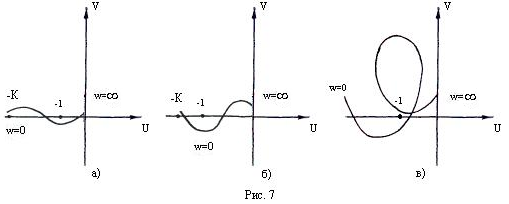 риl=1 пример не рис.7 а) б); а
в случаеl=3 рис.7 в)
риl=1 пример не рис.7 а) б); а
в случаеl=3 рис.7 в)
Начальная точка характеристики на оси абсцисс левее (-1) считается как половина периода.
Построение областей D-разбиения
Метод D-разбиение состоит в том, что для определения границ устойчивости системы аналогично методу Михайлова в характеристическое уравнение
![]()
подставляется
мнимое значение
= jw,
причем w
изменяется от ![]() до
до ![]() .При w
конечном таким образом определяется
колебательная граница устойчивости, а
при частных значениях w=0
и
.При w
конечном таким образом определяется
колебательная граница устойчивости, а
при частных значениях w=0
и ![]() - остальные границы
(соответствующие значениям
- остальные границы
(соответствующие значениям ![]() и
и ![]() ).
).
Однако = jw может быть не только на границе устойчивости. Чтобы получить границу устойчивости, нужно обеспечить еще услоие отсутствия в данном уравнении корней с положительной вещественной частью (иначе система будет не на границе, а попусту неустойчива).
Рассмотрим метод D-разбиения сначала для определения устойчивости по одному параметру, а затем – по двум.
Пусть некоторый параметр К, влияние которого на устойчивость надо выяснить, входит в характеристическое уравнение следующим образом:
![]()
Тогда подстановка = jw дает
![]()
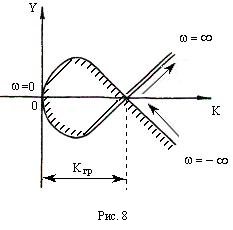
Границей устойчивости будет вещественное значение правой части этого равенства. Чтобы его найти, строим на комплексной плоскости (К,у) годограф функции
![]()
При
![]() и затем
и затем
![]() , как и показано на рисунке 8. Штриховка
кривой производится слева, если идти в
направлении увеличения w.
Точки пересечения годографа с вещественной
осью К определяют границы устойчивости.
В данном случае (рис.8) область устойчивости
будет
, как и показано на рисунке 8. Штриховка
кривой производится слева, если идти в
направлении увеличения w.
Точки пересечения годографа с вещественной
осью К определяют границы устойчивости.
В данном случае (рис.8) область устойчивости
будет
![]()
Для построения на области устойчивости двух каких-нибудь параметров К и Т после подстановки =jwв характеристическое уравнение
![]()
или
![]()
откуда
![]()
![]()
Подставляя
в полученные выражения разные значения
W
сначала
![]() ,
а затем
,
а затем
![]() ,строим по точкам
кривые на плоскости (К,Т). Штриховка
каждой кривой, если идти в сторону
увеличения w,
делается слева, когда якобиан, т.е.
определитель вида
,строим по точкам
кривые на плоскости (К,Т). Штриховка
каждой кривой, если идти в сторону
увеличения w,
делается слева, когда якобиан, т.е.
определитель вида


![]()
![]()
![]()
![]()
![]()
положителен.
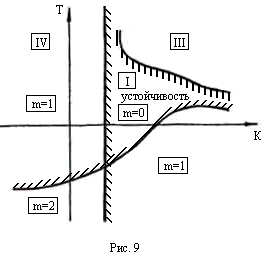
В обратном случае штриховка кривой
производится справа. Если при
![]() кривая пробегается дважды, то штриховка
наносится дважды. (рис. 9). Такие кривые
соответствуют колебательной границе
устойчивости (w
– частота колебания), на которой пара
комплексных корней меняет знак
вещественной части с минуса на плюс.
кривая пробегается дважды, то штриховка
наносится дважды. (рис. 9). Такие кривые
соответствуют колебательной границе
устойчивости (w
– частота колебания), на которой пара
комплексных корней меняет знак
вещественной части с минуса на плюс.
Значениям
w=0
и ![]() соответствуют особые кривые (чаще всего
прямые), вдоль которых w
сохраняет постоянное значение (0 или
соответствуют особые кривые (чаще всего
прямые), вдоль которых w
сохраняет постоянное значение (0 или
![]() ).
Штриховка их (однократная) согласуется
с предыдущей, как показано не рис.8.
Кривые с однократной штриховкой
соответствует переходу вещественного
корня с отрицательного на положительный
через нуль или бесконечность.
).
Штриховка их (однократная) согласуется
с предыдущей, как показано не рис.8.
Кривые с однократной штриховкой
соответствует переходу вещественного
корня с отрицательного на положительный
через нуль или бесконечность.
4.2. Задание на работу
Определить устойчивость разомкнутой системы по критерию Михайлова,
замкнутой системы – по критерию Найквиста.
Построить D – разбиение. (По 1 или 2 параметрам)
4.4. Порядок выполнения работы
Рассмотрим порядок выполнения работы на примере функции:
![]()
Где К=58 с-1-общий коэффициент усиления разомкнутой системы,
![]() =
0,57 с,
=
0,57 с,
![]() =
0,01 с – постоянные времени.
=
0,01 с – постоянные времени.
Для определения устойчивости разомкнутой системы воспользуемся критерием Михайлова.
Характеристический полином замкнутой системы имеет вид:
![]() ;
;
Для построения кривой Михайлова определим вещественную и мнимую части функции L(jw):
![]() ;
;
![]() ;
;
Посмотрим кривую
Михайлова – Y(x)
– при измененииwот 0 до
![]() с помощьюMatLAB
с помощьюMatLAB

>> w=9:1:17
w=
Columns 1 through 12
0 1 2 3 4 5 6 7 8 9 10 11
Columns 13 through 18
13 14 15 16 17
>> plot(58-0.58.*( w.^2),w-0.0057.*( w.^3))
>>


Для определения устойчивости в замкнутом состоянии воспользуемся критерием Найквиста.
Рассмотрим саму функцию W(jw) для построения амплитудно-фазовой частотной характеристики
![]()
Построим А.Ф.Х. Y(x) с помощьюMatLAB

>> w=10:1:500
w=
Columns 1 through 12
10 11 12 13 14 15 16 17 18 19 20 21

Columns 481 through 491
490 491 492 493 494 495 496 497 498 499 500
>> z=58./(i.*w.*(1+i.*w.*0.57).*(1+i.*w.*0.01))
z=
Columns 1 through 4
-0.9945-0.6737i -0.8245-0.0401i -0.694-0.0179i -0.5917-0.0029i

Columns 489 through 491
0.0000 + 0.0001i 0.0000 + 0.0001i 0.0000 + 0.0001i
>> plot(real(z),imag(z))

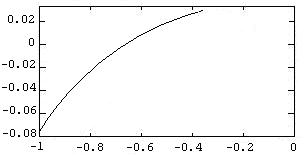
Найдем области устойчивости.
Характеристическое уравнение замкнутой системы имеет вид:
![]()
![]()
![]()
Будем
искать область устойчивости на плоскости
параметров (К,![]() ).
Из написанных уравнений находим (при
w
).
Из написанных уравнений находим (при
w![]() )
)
![]() =
=![]()
![]()
т.е. для нашей функции
![]() =
=![]()
![]()
Построим
кривые на плоскости (К,![]() ),
подставляя в полученные выражения
разные значения w
сначала
),
подставляя в полученные выражения
разные значения w
сначала
![]() ,
а затем
,
а затем
![]() .
.
Для определения направления штриховки запишем якобиан


![]()
![]() <0
при w>0,
<0
при w>0,
![]()
![]()
![]() >0
при w<0.
>0
при w<0.
