1 семестр / Линейная Алгебра / Образец Индивид задание 4_второй поток

Образец индивидуального задания 4.

Для зачета выполнить (и/или проверить себя в МАТЛАБЕ) любые три задачи. Одна задача 2 балла. Непосредственного опроса не будет. Опрос заменит ваша письменная часть этой работы. Вся работа максимум 10 баллов.

Необходимую теорию читаем в СРС (модуль 2)+лекции Ржавинской (книжка)+МАТЛАБ ищем нужные команды самостоятельно.

1. Вычислить ранг матрицы методом элементарных преобразований в МАТЛАБе, используя

двоеточие для работы со строками.

ИЛИ 1. Вычислить определитель методом приведения к треугольному виду

и разложением по строке или столбцу. Проверить себя встроенной функцией det

2. Найти обратную матрицу методом элементарных преобразований в МАТЛАБе

найти A-1, если 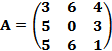. Сделать проверку. A*A-1=E, обращаясь с помощью индексов к элементам матрицы.

3. Найти собственные числа и собственные векторы линейного оператора, заданного матрицей .

Сначала найти на листочке, затем с помощью встроенных команд МАТЛАБа проверьте себя.

(Найдите в Кривилеве нужную команду, которая дает матрицу из собственных значений и собственных векторов)

4. В линейном пространстве L₃ заданы векторы в некотором базисе. Доказать, что векторы составляют базис, найти матрицу перехода и координаты вектора в базисе . .

5. Заданы векторы в некотором базисе. Проверить, что векторы составляют базис. Применяя процесс ортогонализации Грама-Шмидта построить новый ортогональный базис. .

Затем найдите ортонормированный базис.

Задачу сначала решить на листочке. Опорные вычисления проверяйте на МАТЛАБЕ. Затем проиллюстрируйте на МАТЛАБ. Все векторы изобразить в МАТЛАБЕ. Новые векторы изобразите зелеными линиями, старые желтыми линиями, вспомогательные тонкими синими. Орты нового базиса изобразите красным.