Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_EGE_2010_Zadania_tipa_S1-S5_Metod

.pdf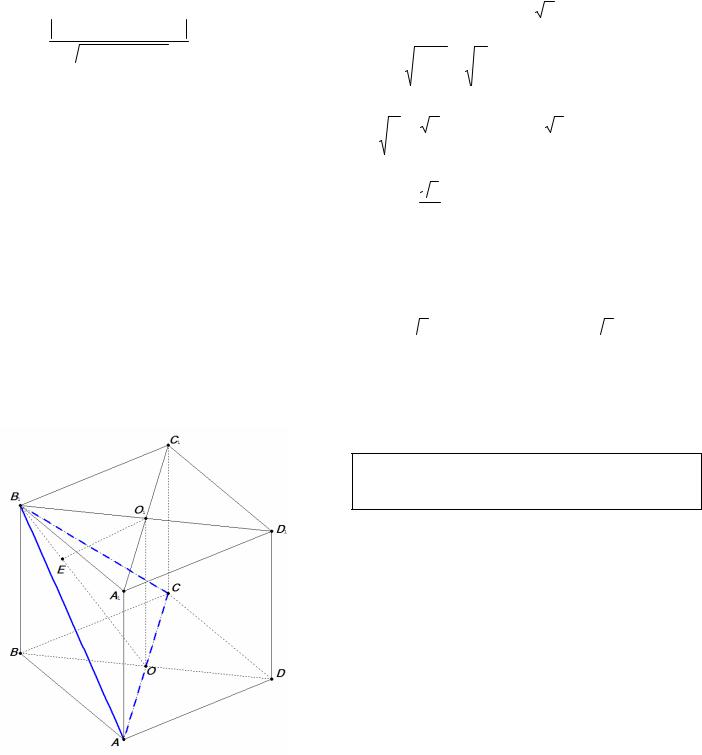

Скачиваний:

Добавлен:

05.06.2015

Размер:

3.32 Mб

Скачать

☆

<<< < Предыдущая 12 / 152 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

5) вычисляется по формуле

ρ(M ;α)= Ax0 + By0 +Cz0 + D , где

A2 + B2 +C 2

M (x0 ; y0 ; z0 ), плоскость α задана уравнением

Ax + By +Cz + D = 0 ;

6)находится с помощью векторного метода;

7)находится с помощью координатновекторного метода.

Пример 3. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки С1 до плоскости

АВ1С .

Решение. Так как прямая А1С1 параллельна АС, то прямая А1С1 параллельна плоскости АВ1С (рис. 2). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой А1С1 до плоскости АВ1С . Например, расстояние от центра О1 квадрата A1 B1C1 D1 до плоскости АВ1С равно h.

Рис. 2

Пусть Е – основание перпендикуляра, опущенного из точки О1 на прямую В1О, где О –

центр квадрата ABCD . Прямая О1 Е лежит в плоскости BB1 D1 D , а прямая АС перпендикулярна этой плоскости. Поэтому О1 Е АС и О1 Е - перпендикуляр к плоскости АВ1С , а

О1 Е = h .

Так				как		В О =			2		,		О О =1,	то
Так				как		В О =					,		О О =1,	то
						1		1	2			1
									2
ОВ =			1	+1 =		3	.	Выражая двумя способами
ОВ =				+1 =			.	Выражая двумя способами
	1		2			2
			2			2						В1О1О, получим
площадь					треугольника							В1О1О, получим
h		3	=	2	1 , откуда h =					3			.
h	2		=	2	1 , откуда h =								.
	2			2					3

Ответ: 33 .

1. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если

AD = 2 5, AB = AC =10, BC = 4 5.

Ответ: 2.

4. Расстояние между скрещивающимися прямыми

Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.

Расстояние между скрещивающимися прямыми

1)равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой;

2)равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые;

3)равно ρ(a;b)= ρ(A;b1 ), где A = aα , b1 = bα : если ортогональная проекция на плоскость α переводит прямую а в точку А, а прямую b в

прямую b1 , то расстояние между скрещивающимися прямыми а и b равно расстоянию от


точки А до прямой b1 ;
4)	вычисляется		по	формуле
ρ(AB;CD)=		6VABCD	где А	и В – точки
ρ(AB;CD)=		AB CD sin ϕ	где А	и В – точки

на одной прямой, С и D – точки на другой прямой, ϕ - угол между данными прямыми;

5)определяется с помощью векторного метода;

6)определяется с помощью координатновекторного метода.

Пример 4. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите расстояние между прямыми BD и SA.

Решение. Пусть Е – основание перпендикуляра (рис. 3), опущенного из точки О на ребро SA. Так как прямая BD перпендикулярна плоскости

AOS, то BD OE .

Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA.

Найдем его длину, вычислив двумя способа-

ми площадь треугольника AOS.
Из			равенства	AO SO = AS OE, где
AO =	2		, AS =1,	SO =	2	следует, что
AO =	2		, AS =1,	SO =	2	следует, что
	2				2
OE =	1	.
OE =	2	.
	2

Рис. 3

Ответ: 0,5.

1. В пирамиде DABC известны длины ребер:

AB = AC = DB = DC =10, BC = DA =12. Най-

дите расстояние между прямыми DA и ВС.

Ответ: 2 7.

5.Угол между двумя прямыми

•Углом между двумя пересекающимися пря-

мыми называется наименьший из углов, образованных при пересечении прямых.

•0D < (a;b)≤ 90D .

•Углом между скрещивающимися прямыми

называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

•Две прямые называются перпендикулярными, если угол между ними равен 90D .

•Угол между параллельными прямыми счита-

ется равным нулю.

•При нахождении угла между прямыми используют:

1) формулу cosϕ =	b2	+c2 −a2	для нахожде-

		2bc
		2bc
ния угла ϕ между прямыми m и			l , если сторо-

ны а и b треугольника АВС соответственно параллельны этим прямым;

2) формулу

cosϕ =

или в координатной

форме

x1 x2 + y1 y2

+ z1 z2

cosϕ =

для на-

+ y2 + z2 x2

+ y 2

+ z2

хождения угла ϕ между прямыми m и l , если

векторы p(x1 ; y1 ; z1 ) и q(x2 ; y2 ; z2 ) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы

p q = 0 или x1 x2 + y1 y2 + z1 z2 = 0 ; 3) ключевые задачи.

Пример 5. В кубе ABCDA1 B1C1 D1 найдите угол между прямыми A1 D и D1 E , где Е – середина ребра CC1 .

Решение. Пусть F – середина ребра ВВ1 , а – ребро куба, ϕ - искомый угол.

Так как A1 F D1 E , то ϕ - угол при вершине

A1 в треугольнике A1 FD .

Из треугольника BFD имеем

FD	2		= BD			2		+ BF			2	= 2a			2	+		a2				=		9a2		, а из тре-
FD			= BD					+ BF				= 2a				+			4			=			4	, а из тре-
																			4						4
угольника A1 B1 F получаем
A F		2	= A B					2		+ B F			2	= a		2	+			a2			=		5a	2	, откуда
A F			= A B							+ B F				= a			+						=				, откуда
1					1	1					1								4						4
																			4						4
A F =				a	5		.
A F =							.
1			2
			2
Далее в треугольнике A1 FD используем теоре-
му косинусов
FD	2 = A D2								+ A F 2				−2A D A F cosϕ ,
			1							1						1			1
9a2		= 2a			2	+			5a2		− 2a			2			a 5					cosϕ , откуда
4		= 2a				+				4	− 2a			2				2				cosϕ , откуда
4										4								2
cosϕ =					1				и ϕ = arccos									1			.
cosϕ =					10				и ϕ = arccos									10			.
					10													10

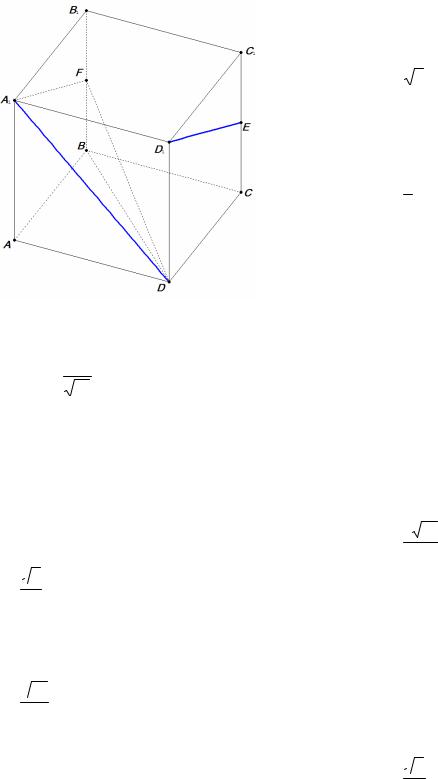
Рис. 4

Ответ: arccos 110 .

1. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и B1C1 . Найдите ко-

синус угла между прямыми АЕ и BF.

Ответ: 0,8.

2. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и C1 D1 . Найдите косинус угла между прямыми АЕ и BF.

Ответ: 55 .

3. В кубе ABCDA1 B1C1 D1 точка Е – середина ребра A1 В1 . Найдите косинус угла между прямыми АЕ и ВD1 .

Ответ: 515 .

4.К диагонали куба провели перпендикуляры из остальных вершин куба. На сколько частей и в каком отношении основания этих перпендикуляров разделили диагональ?

Ответ: на три части в отношении 1:1:1.

5.К диагонали A1C куба ABCDA1 B1C1 D1 про-

вели перпендикуляры из середин ребер АВ и AD. Найдите угол между этими перпендикулярами.

Ответ: 60D .

6. К диагонали A1C куба ABCDA1 B1C1 D1 про-

вели перпендикуляры из вершин А и В. Найдите угол между этими перпендикулярами.

Ответ: 60D .

7. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите

косинус угла между прямыми АВ и A1C .

Ответ:	2	.
	4
8. В
	правильной треугольной		призме
ABCA1 B1C1 , все ребра которой равны 1, найдите
косинус угла между прямыми AВ1 и			BC1 .

Ответ: 14 .

9. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда образуют с плоскостью его основания углы ϕ и ψ. Найдите угол между этими диагоналями.

Ответ: arccos(sin ϕ sinψ )

10. В правильной треугольной	призме
ABCA1 B1C1 , все ребра которой равны 1, точки D,
Е – середины ребер соответственно A1 В1	и B1C1 .

Найдите косинус угла между прямыми АD и

ВЕ. Ответ: 0,7.

11. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D

– середина ребра A1 В1 . Найдите косинус угла между прямыми АD и BC1 .

Ответ: 32010 .

12. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BC1 .

Ответ: 0,75.

13. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BD1 .

Ответ: 42 .

14. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BE1 .

Ответ: 90D .

15. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, точки G, H – середины ребер соответственно A1 В1 и B1C1 . Найдите косинус угла между прямыми АG и BH.

Ответ: 0,9.

16. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите косинус угла между прямыми АG и BC1 .

Ответ: 104 .

17. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите косинус угла между прямыми АG и BD1 .

Ответ: 55 .

18. Найдите угол между непересекающимися медианами граней правильного тетраэдра.

Ответ: arccos 16 ; arccos 23 .

19. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки Е, F – середины ребер соответственно SB и SC. Найдите косинус угла между прямыми АЕ и BF.

Ответ: 16 .

20. Ребра АD и ВС пирамиды DABC равны 24 см и 10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми АD и ВС.

Ответ: 90D .

6.Угол между прямой и плоскостью

•Углом между плоскостью и не перпендику-

лярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.

•0D < (a;α) <90D .

•Угол между взаимно перпендикулярными прямой и плоскостью равен 90D .

•Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается рав-

ным 0D .

Угол между прямой l и плоскостью α можно вычислить:

1)если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;

2)по формуле sin ϕ = sin (l;α)= ρ(AMM ;α), где

M l , l ∩α = A;

3) по формуле

sin ϕ =

или в координат-

ной форме

x1 x2 + y1 y2 + z1 z2

sin ϕ =

, где

+ y2

+ z2

+ y 2

+ z2

n(x1 ; y1 ; z1 )- вектор нормали плоскости α , p(x2 ; y2 ; z2 )- направляющий вектор прямой l;

• прямая l и плоскость α параллельны тогда и только тогда, когда x1 x2 + y1 y2 + z1 z2 = 0 ;

4)используя векторный метод;

5)используя координатно-векторный метод;

6)используя ключевые задачи.

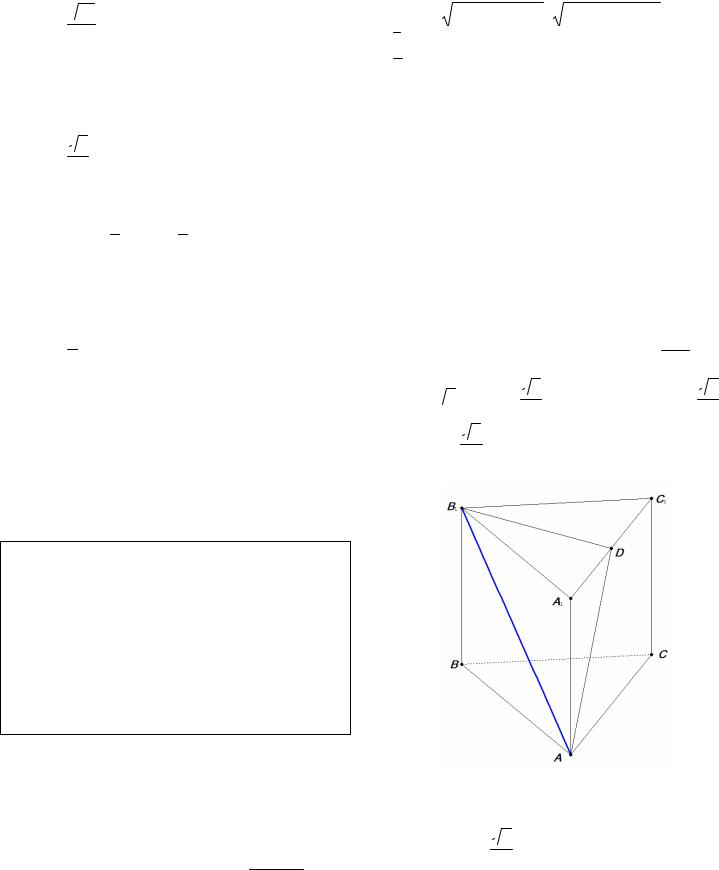
Пример 6. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите

угол между прямой АВ1 и плоскостью АА1С1С . Решение. Пусть D – середина А1С1 , тогда B1 D - перпендикуляр к плоскости АА1С1С , а D – проекция точки В1 на эту плоскость (рис. 5).

Если ϕ - искомый угол, то sin ϕ = B1 D , где

AB1

AB1 = 2 , B1 D = 23 , и поэтому sinϕ = 46 ,

ϕ = arcsin 46 .

Рис. 5

Ответ: arcsin 46 .

Ответ:

10. В

В кубе

ABCDA1 B1C1 D1 найдите угол между

прямой AВ1

и плоскостью ABC1 .

Ответ: 30D .

В кубе

ABCDA1 B1C1 D1 найдите тангенс угла

между прямой AA1

и плоскостью BC1 D .

Ответ:

В кубе

ABCDA1 B1C1 D1 найдите тангенс угла

между прямой AC1

и плоскостью BCC1 .

Ответ:

ABCDA1 B1C1 D1 точка Е – середина

В кубе

ребра A1 В1 . Найдите синус угла между прямой

АЕ и плоскостью ВDD1 .

Ответ:

ABCDA1 B1C1 D1 точка Е – середина

В кубе

ребра A1 В1 . Найдите синус угла между прямой

АЕ и плоскостью ВDC1 .

Ответ:

прямоугольном

параллелепипеде

ABCDA1 B1C1 D1 найдите угол между плоскостью

AA1C и прямой

A1 В, если

AA1 = 3 ,

AB = 4 ,

BC = 4.

Ответ: arcsin

2 2

прямоугольном

параллелепипеде

ABCDA1 B1C1 D1 найдите угол между плоскостью

A1 BC и прямой

BC1 , если

AA1 = 8 ,

AB = 6 ,

BC =15 .

Ответ: arcsin 8524 .

8.В прямоугольном параллелепипеде

ABCDA1 B1C1 D1 , у которого AA1 = 4 , A1 D1 = 6 ,

C1 D1 = 6 найдите тангенс угла между плоскостью ADD1 и прямой EF, проходящей через середины ребер АВ и B1C1 .

Ответ: 53 .

9.В прямоугольном параллелепипеде

ABCDA1 B1C1 D1 , у которого AB = 4 , BC = 6 , CC1 = 4 найдите тангенс угла между плоскостью АВС и прямой EF, проходящей через середины ребер AA1 и C1 D1 .

1 . 10

правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D

– середина ребра A1 В1 . Найдите синус угла между прямой АD и плоскостью BСC1 .

Ответ:		15		.
Ответ:				.
		10
11. В основании прямой призмы							MNKM1 N1 K1
лежит прямоугольный треугольник MNK, у ко-
торого угол				N равен 90D , угол			M равен 60D ,
NK =18 .		Диагональ боковой грани						M1 N со-
ставляет угол 30D с плоскостью							MM1 K1 . Най-
дите высоту призмы.
Ответ: 6 6 .
12. В основании прямой призмы ABCA1 B1C1 ле-
жит прямоугольный треугольник							АВС, у кото-
рого угол			С		равен 90D , угол		А	равен 30D ,
AC =10		3 . Диагональ боковой грани B1C со-
ставляет угол 30D с плоскостью AA B . Найдите
высоту призмы.							1	1
высоту призмы.
Ответ: 10 2 .
Критерии:
	Содержание критерия						Баллы
	Обоснованно получен					вер-		2
	ный ответ.							2
	ный ответ.
	Способ			нахождения		иско-
	мой величины верен, но по-							1
	лучен	неверный ответ или						1
	лучен	неверный ответ или
	решение не закончено.
	Решение				не соответствует
	ни одному из критериев, пе-							0
	речисленных выше.

13. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите синус угла между прямой АG и BСС1 .

Ответ: 1015 .

14. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите синус угла между прямой АG и BDD1 .

Ответ: 55 .

15. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите ко-

синус угла между прямой АВ и плоскостью

SAD.

Ответ: 33 .

16. В правильной шестиугольной пирамиде SABCDEF, боковые ребра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой АС и плоскостью SAF.

Ответ: 55 .

7.Угол между плоскостями

•Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.

•Величина двугранного угла принадлежит

промежутку (0D;180D ).

•Величина угла между пересекающимися плоскостями принадлежит промежутку (0D;90D ].

•Угол между двумя параллельными плоско-

стями считается равным 0D .

Угол между пересекающимися плоскостями можно вычислить:

1)как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;

2)как угол треугольника, если удается включить линейный угол в некоторый треугольник;

3)по формуле (M ; β), где

ρM ;lsin (α; β)= ρ ( )

M α; α ∩β = l ;

4) по формуле cos (α; β)= SS′ , где S – площадь

фигуры Ф, расположенной в плоскости α , S′ - площадь проекции фигуры Ф на плоскость β ;

5) как угол между перпендикулярными им прямыми;

6) по формуле cos (α; β)=

или в коор-

cos (α; β)

динатной форме

A1 A2 + B1 B2 +C1C2

где

+ B2

+C2

A2 + B

+C2

n1 (A1 ; B1 ;C1 ) - вектор нормали плоскости

A1 x + B1 y +C1 z + D1 = 0 , n2 (A2 ; B2 ;C2 ) - вектор нормали плоскости A2 x + B2 y +C2 z + D2 = 0 ; 7) используя ключевые задачи.

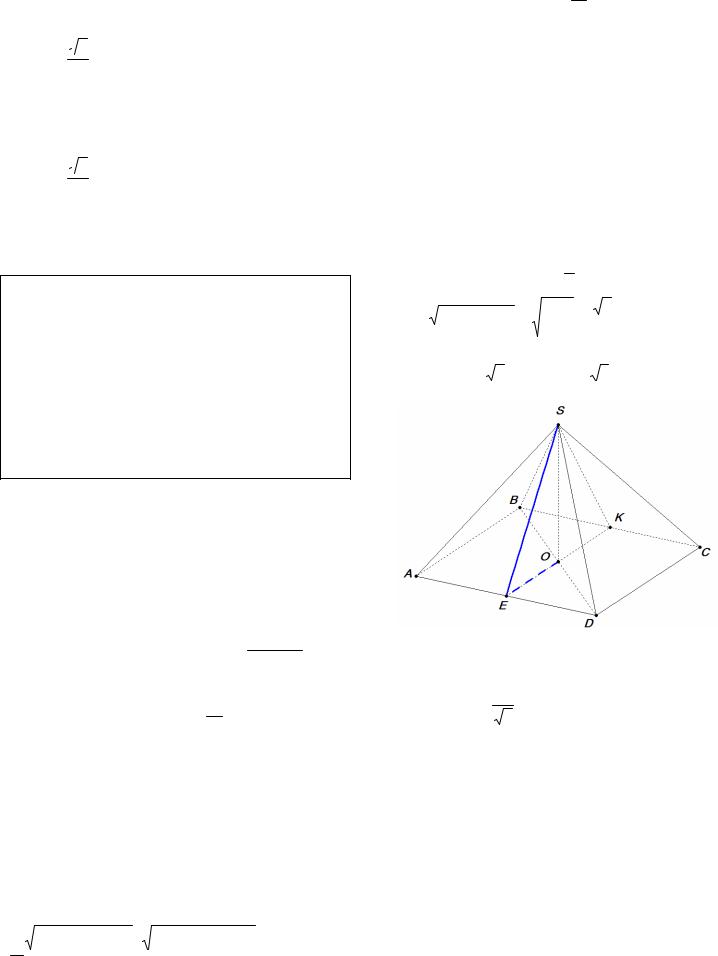
Пример 7. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите двугранный угол между основанием и боковой гранью.

Решение. Пусть Е и К – середины ребер AD и BC соответственно, О – центр основания ABCD (рис. 6). Тогда SE AD , EK AD и поэтомуSEK =ϕ - линейный угол данного двугранно-

го угла.

Так как AD =1, OE = 12 , SD =1, то

SE = SD2 − ED2 =						1 −	1	=	3		,
							4		2
		OE
cosϕ	=		=	1	, ϕ = arccos				1	.
		SE		3					3

Рис. 6

Ответ: arccos 13 .

1. Дан куб ABCDA1 B1C1 D1 . Найдите угол между плоскостями AB1C1 и A1 B1C .

Ответ: π3 .

2. Диагональ A1C куба ABCDA1 B1C1 D1

служит ребром двугранного угла, грани которого проходят через середины ребер АВ и DD1 . Найдите величину этого угла.

Ответ: 120D .

3. Диагональ A'C куба ABCDA' B'C' D' служит ребром двугранного угла, грани которого проходят через В и D . Найдите величину этого угла.

Ответ: 120D .

4. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и A1 D1 . Найдите тангенс угла между плоскостями АЕF и ВCC1 .

Ответ: 25 .

5. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и A1 D1 . Найдите тангенс угла между плоскостями АЕF и ВDD1 .

Ответ:	2	.
	4

6. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 известны длины ребер:						AA1 = 5,
AB =12,	AD = 8.				Найдите тангенс угла между
плоскостью				АВС	и плоскостью, проходящей
через точку				В перпендикулярно прямой АК,
если К - середина ребра C1 D1.
Ответ: 2.
7. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 , у					которого AB = 4 ,	BC = 6 ,
CC1 = 4	найдите				тангенс угла между плоско-
стями CDD1 и BDA1 .
Ответ:	3 2		.

	2
8. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 , у					которого AB = 6 ,	BC = 6 ,
CC1 = 4	найдите				тангенс угла между плоско-
стями ACD1				и A1 B1C1 .

Ответ: 2 32 .

9. Основание прямой четырехугольной призмы ABCDA1 B1C1 D1 - прямоугольник ABCD , в кото-

ром АВ = 5 , AD =	33 . Найдите тангенс угла
между плоскостью	грани AA1 D1 D призмы и

плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1 D , если рас-

стояние между прямыми A1C1 и BD равно 3 .

Ответ: 1,2.

10. Основание прямой четырехугольной призмы ABCDA1 B1C1 D1 - прямоугольник ABCD , в кото-

ром АВ =12 , AD = 31 . Найдите тангенс угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1 , если расстояние

между прямыми AC и B1 D1 равно 5.

Ответ: 42 .

11. Сторона основания правильной треугольной призмы ABCA1 B1C1 равна 2, а диагональ боко-

вой грани равна 5 . Найдите угол между плоскостью A1 BC и плоскостью основания призмы.

Ответ: 30D .

12. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите угол между плоскостями

ACВ1 и A1С1 В.

Ответ: arccos 17 .

13. (Демо 2010) Сторона основания правильной

треугольной призмы				ABCA1 B1C1 равна 2, а диа-
гональ боковой грани равна						5 . Найдите угол
между плоскостью				A1 BC и плоскостью основа-
ния призмы.
Ответ: 30D .
14.	В	правильной			треугольной			призме
ABCA1 B1C1 , все ребра которой равны 1, точки D,
Е – середины ребер соответственно A1 В1								и А1C1 .
Найдите тангенс угла между плоскостями АDЕ
и ВCC1 .
Ответ:		3	.
		4

15. Основанием прямой треугольной
призмы ABCA1 B1C1 является равнобедренный
треугольник АВС,				в	котором		AB = BC =10,
AC =16. Боковое ребро призмы равно 24. Точка
Р – середина ребра BB1 . Найдите тангенс угла
между плоскостями				A1 B1C1		и АСР.
Ответ: 2.
16. Основанием прямой треугольной
призмы ABCA1 B1C1 является равнобедренный
треугольник АВС,				в	котором		AB = BC = 20,
AC = 32. Боковое ребро призмы равно 24. Точка
Р	принадлежит			ребра		BB1 ,		причем
BP : PB1		=1 : 3. Найдите тангенс					угла	между

плоскостями A1 B1C1 и АСР.

Ответ: 0,5.

17. Основанием прямой треугольной

призмы ABCA1 B1C1 является треугольник АВС, в котором AB = AC = 8, а один из углов равен 60D . На ребре AA1 отмечена точка Р так, что AP : PA1 = 2 :1. Найдите тангенс угла между плоскостями АВС и СВР, если расстояние между прямыми АВ и C1 B1 равно 18 3 .

Ответ: 3.

18. Основанием прямой треугольной

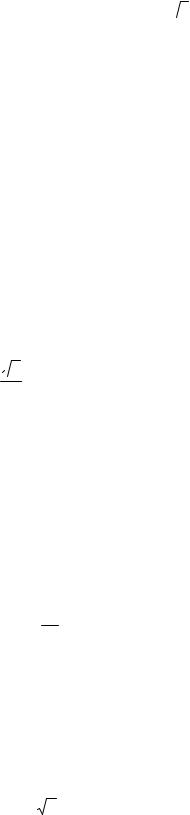
призмы ABCA1 B1C1 является треугольник АВС, в котором AC = BC = 6, а один из углов равен 60D . На ребре CC1 отмечена точка Р так, что CP : PC1 = 2 :1. Найдите тангенс угла между плоскостями АВС и АВР, если расстояние между прямыми АС и A1 B1 равно 18 3 .

Ответ: 4.

19. Основанием прямой призмы

ABCA1 B1C1 является прямоугольный треугольник АВС с гипотенузой АС. Найдите тангенс угла между плоскостью A1 B1C1 и плоскостью, проходящей через середину ребра AA1 и пря-

мую ВС, если AB = 4,	BB1 =12.
Ответ: 1,5.
20. Основание пирамиды DABC - равнобедрен-
ный треугольник	АВС, в котором

AB = BC =13, AC = 24. Ребро DB перпендику-

лярно плоскости основания и равно 20. Найдите тангенс двугранного угла при ребре АС.

Ответ: 4.

21. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями АВС и BCS.

Ответ: 33 .

22.Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

Ответ: 2 или 14.

23.Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

Ответ: 3 или 1721 .

8.Разные задачи

1.Найдите радиус сферы, внутри которой расположены четыре шара радиуса r. Каждый из этих шаров касается трех других и поверхности сферы.

		6
Ответ: r 1	+		.
Ответ: r 1	+		.
		2
		2

2. Три сферы, попарно касаясь друг друга, касаются плоскости треугольника в его вершинах. Найти радиусы сфер, если

стороны треугольника равны а, b и с.

Ответ:			ab	;	bc	;	ac	.
					2a
			2c				2b
3. Плоскость пересекает боковые ребра									SA, SB
и	SC	треугольной пирамиды SABC							в точках
K,	L и	M соответственно. В каком отношении

делит эта плоскость объем пирамиды, если из-

вестно,	что			SK	=	SL	= 2 , а медиану SN тре-
вестно,	что			KA	=	LB	= 2 , а медиану SN тре-
				KA		LB
угольника SBC эта плоскость делит пополам.
Ответ:		8	.
Ответ:	37		.
	37

4. Найти угол при вершине в осевом сечении конуса, если на его поверхности можно провести три попарно перпендикулярные образующие.

		1
Ответ: arccos	−		.
Ответ: arccos	−	3	.
		3

5. Какие значения принимает угол между образующими конуса, если его образующая в два раза больше радиуса основания?

Ответ: (0D;60D ].

9. Координатный метод

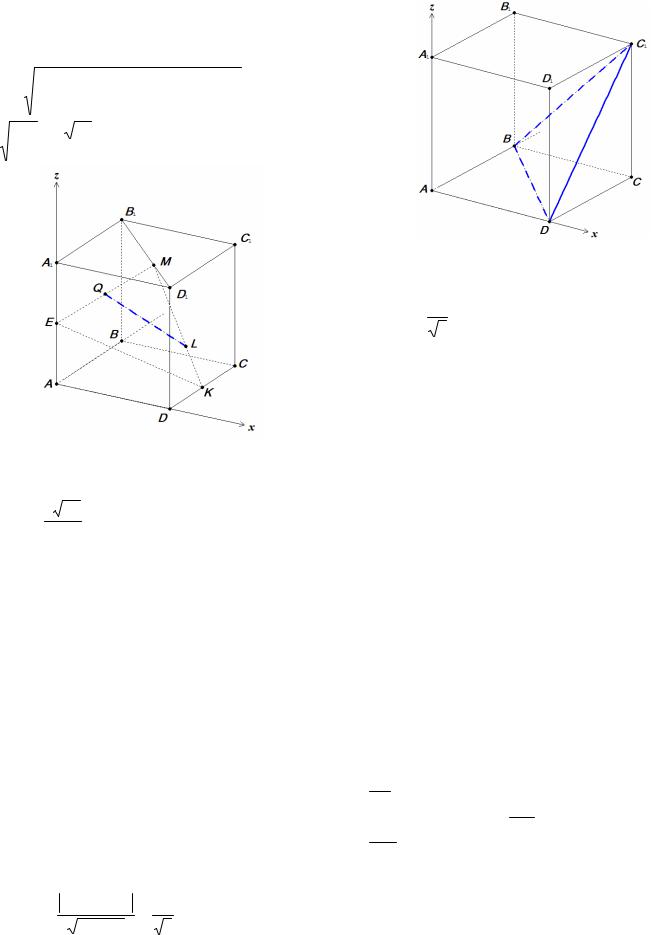
Пример 8. В единичном кубе ABCDA1 B1C1 D1 точки Е и К - середины ребер AA1 и CD соответственно, а точка М расположена на диагонали B1 D1 так, что B1M = 2MD1. Найдите рас-

стояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что

ML = 2LK.

Решение. Введем прямоугольную систему координат, как указано на рисунке 7. Тогда

	1			1
Е 0;0;		,	К 1;		;0 ,	В (0;1;1) ,	D (1;0;1) . Для
Е 0;0;	2	,	К 1;	2	;0 ,	В (0;1;1) ,	D (1;0;1) . Для
	2			2		1	1

нахождения координат точки М используем

формулу

координат точки,

делящей

отрезок

B1 D1

отношении

2:1.

Имеем

0 + 2 1

1 + 2 0

1 + 2 1

;

;1 . Анало-

1 + 2

1 +

1 + 2

гично получим координаты точки L, делящей

отрезок

МК

отношении

2:1.

Имеем

+ 2 1

+ 2

1 + 2 0

;

Коор-

1 + 2

динаты точки Q равны полусуммам соответст-

вующих

координат

точек Е и

М,

поэтому

1 +1 +1

ρ(А1 ; β)=

0 +0 −1 −1

А1 (0;0;1)

ние от точки

	1			1			3
Q			;		;			. Применим формулу для расстояния
Q	3		;	6	;		4	. Применим формулу для расстояния
	3			6			4
между точками с заданными координатами
QL =					1					8	2	1		4	2	3		1	2
								−				+	−			+	−		=
							3	−		9		+	−	9		+	−	3	=
							3			9		6		9		4		3
=		725				=			5 29			.
	362									36

Рис. 7

Ответ: 5 3629 .

Пример 9. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки А1 до плоскости

BDC1 .

Решение. Составим уравнение плоскости, проходящей через точки B(0;1;0) , D(1;0;0) и

C1 (1;1;1) . Для этого подставим координаты этих

точек в общее уравнение плоскости

Ax + By +Cz + D = 0 . Получим систему уравнений

B + D = 0			B = −D
		или		Отсюда нахо-
A + D = 0		или	A = −D	Отсюда нахо-
	+ D = 0
A + B +C	+ D = 0		C = D

дим уравнение − Dx − Dy + Dz + D = 0 или

x + y − z −1 = 0 . По формуле находим расстоядо плоскости β = BDC1 :

= 23 .

Рис. 8

Ответ: 23 .

10. Координатно-векторный метод

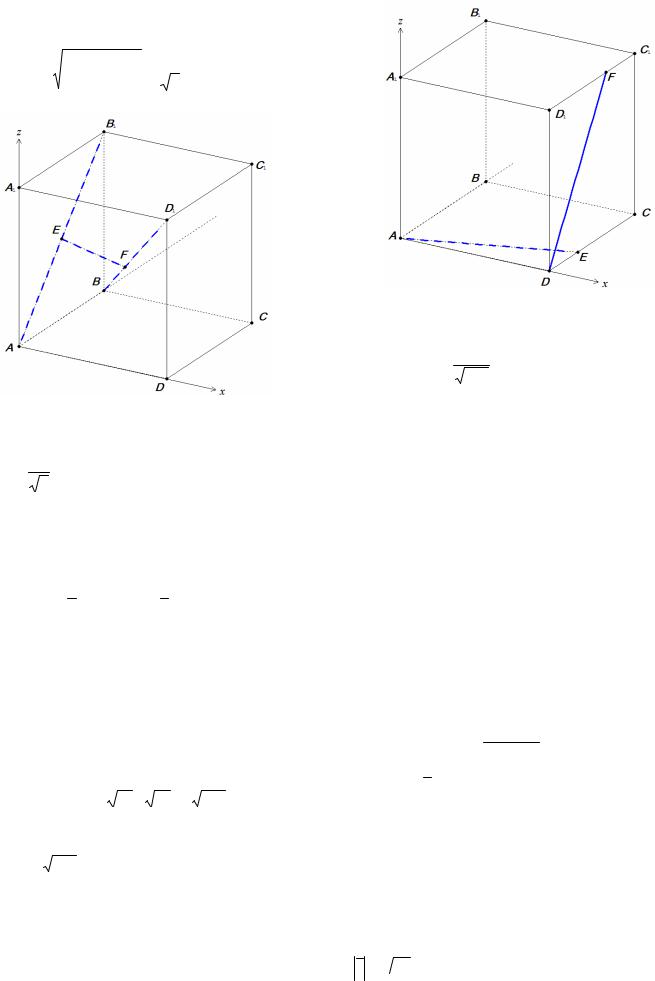
Пример 10. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .

Решение. Введем прямоугольную систему координат (рис. 9), тогда

А(0;0;0) , В(0;1;0) ,				В1 (0;1;1) , D1 (1;0;1) .
Пусть EF – общий перпендикуляр скрещиваю-
щихся прямых BD1				и AB1 , то есть EF AB1 ,
EF BD1 , причем E AB1 и F BD1 . Обозна-
чим λ =	AE	, μ =		BF	и воспользуемся фор-
	B E
			D F
1				1

мулами для координат точки, которая делит данный отрезок в заданном отношении. Полу-

чим E 0;

;

, F

;

1 +λ 1 + λ

+ μ 1

+ μ

1 +

Пусть

= p ,

= q , тогда

E(0; p; p) ,

1 + μ

F(q;1 −q; q) . Так как вектор

EF = (q; 1 −q − p; q − p) должен быть перпендикулярным векторам AB1 = (0;1;1) и

BD1 = (1; −1; 1) , то имеем систему уравнений:

= 0

1 −q − p + q − p = 0

или

= 0

q −1

+ q + p + q − p

= 0

p =

q =


					1		1			1
					1		1			1
Отсюда EF =						;		; −				,
Отсюда EF =					3	;	6	; −		6		,
					3		6			6
				1			1				1			1	.
EF =		=			+				+				=
	EF
	EF		9				36			36				6
			9				36			36				6

Рис. 9

Ответ: 16 .

Пример 11. В единичном кубе ABCDA1 B1C1 D1 найдите угол между прямыми АЕ и DF, где Е и F – точки, расположенные на ребрах CD и C1 D1

так, что DE = 13 DC , C1 F = 13 C1 D1 .

Решение. Введем прямоугольную систему координат, как указано на рисунке 10. Тогда

	А(0;0;0) , D(1; 0; 0) ,											1				2
										Е 1;			; 0 , F 1;				;1 ,
										Е 1;		3	; 0 , F 1;			3	;1 ,
												3				3
		1										2
		1										2
	AE = 1;			; 0	, DF				= 0;				;1 ,
	AE = 1;	3		; 0	, DF				= 0;			3	;1 ,
		3										3
												2
			AE DF									2			2
cosα =			AE DF					=				9		=	2			,

											10		13		130

		AE				DF
									3				3
					2				3				3
α = arccos					2		, где α - искомый угол.
α = arccos							, где α - искомый угол.
				130

Рис. 10

2 Ответ: arccos 130 .

Пример 12. В единичном кубе ABCDA1 B1C1 D1 найдите угол между прямой АD1

иплоскостью α, проходящей через точки А1 , Е

иF, где точка Е – середина ребра C1 D1 , а точка F лежит на ребре DD1 , так, что D1 F = 2DF .

Решение. Введем прямоугольную систему координат, как указано на рисунке 11. Тогда

	А(0;0;0) ,				А1 (0; 0;1) ,						D1 (1; 0;1) ,					1
														Е 1;				;1 ,
														Е 1;		2		;1 ,
																2
		1														1
		1					АD = (1; 0;1),						A E =			1
	F 1; 0;		,												1;		; 0 ,
	F 1; 0;		,												1;	2	; 0 ,
		3						1					1			2
					2
	А1 F =			−	2						n = (x; y; z)
		1; 0;				.		Пусть						-	вектор,
		1; 0;				.		Пусть						-	вектор,
					3
перпендикулярный плоскости α,													ϕ -		искомый

угол. Тогда sin ϕ									=	AD1	n	.


										AD	n
									1

Вектор n найдем из условий перпендикулярности этого вектора векторам

A1 E и А1 F , т.е. из условий

x +

= 0

y = −2x

n A E = 0

или

Пусть

A F

= 0

z =1,5x.

z = 0

x −

x = 2 ,

тогда y = −4 ,

z = 3

= (2; −4;3) ,

n = 29 .

<<< < Предыдущая 12 / 152 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.2019162.54 Кб5Makroekonomika_lektsii.docx
#
05.06.2015323.03 Кб25Marketing_1.docx
#
04.05.20193.24 Mб7mat-analiz-1-kurs.doc
#
17.11.2018586.75 Кб4matan.doc
#
05.06.20151.16 Mб7MatanKoll_1.doc
#
05.06.20153.32 Mб63Matematika_EGE_2010_Zadania_tipa_S1-S5_Metod.pdf
#
05.06.2015575.26 Кб37Matematika_EGE_2010_Zadania_tipa_S6_Metody_r.pdf
#
27.09.2019295.67 Кб5Material.docx
#
04.11.2018145.41 Кб15MatLab Лаб №2.doc
#
05.06.2015285.57 Кб25MATLAB_Практикумы 3_4.docx
#
05.06.20151.23 Mб214Mat_Analiz.docx