
Matematika_EGE_2010_Zadania_tipa_S1-S5_Metod
.pdf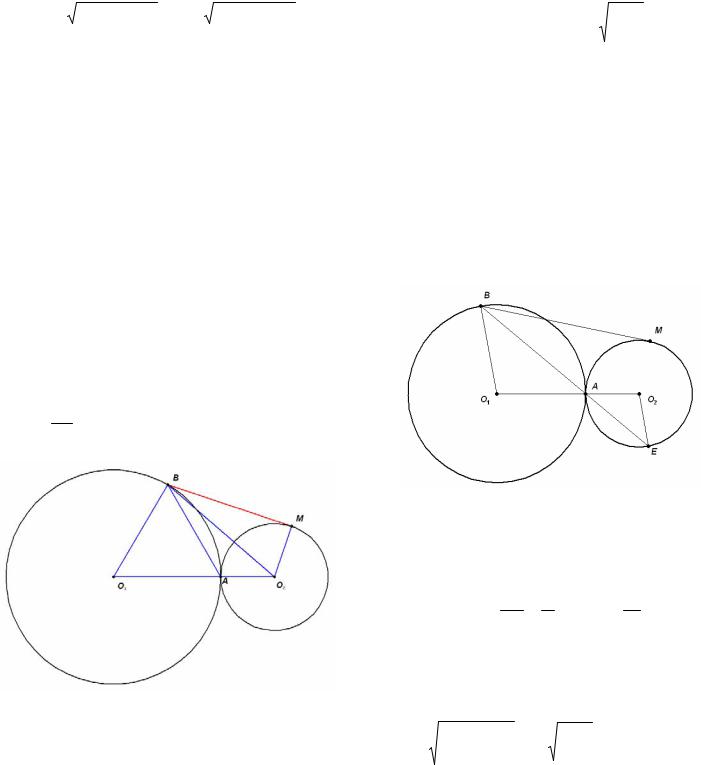
Ответ: a2 −(R −r)2 или a2 −(R +r)2 .
Касающиеся окружности (внешнее или внутреннее касание)
Пример 22. (2010) Окружности S1 и S2 радиусов R и r (R > r) соответственно касаются в точке А. Через точку В, лежащую на окружности S1 , проведена прямая, касающаяся окружности S2 в точке М. Найдите ВМ, если известно, что AB = a.
Первое решение. 1) Окружности касаются внешним образом. Пусть O1 и O2 - центры ок-
ружностей S1 и S2 соответственно, а
O1 AB =ϕ.
Применим теорему косинусов для треугольника
O1 AB : O1B2 = O1 A2 + AB2 −2O1 A ABcosϕ или
R2 = R2 + a2 −2Racosϕ. Отсюда получим cosϕ = 2aR .
Теперь используем теорему косинусов для треугольника O2 AB :
O B2 |
=O A2 |
+ AB2 +2O A AB cosϕ |
или |
|
||||||||
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
O B2 |
= r2 + a2 + 2r acosϕ . Подставим |
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
cosϕ = |
a |
и получим O B |
2 |
= r |
2 |
+a |
2 |
+ |
a2r |
. |
||
|
|
|
|
|
|
|||||||
|
|
2R |
2 |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из прямоугольного треугольника O2 BM
( O2 BM =90D) , используя теорему Пифагора, находим
BM 2 = O2 B2 −r2 = r2 + a2 + a2r −r2 = R
2 |
|
|
r |
|
BM = a 1+ |
r |
. |
|
= a |
1 |
+ |
|
. |
Отсюда |
|
||
|
R |
|||||||
|
|
|
R |
|
|
|
||
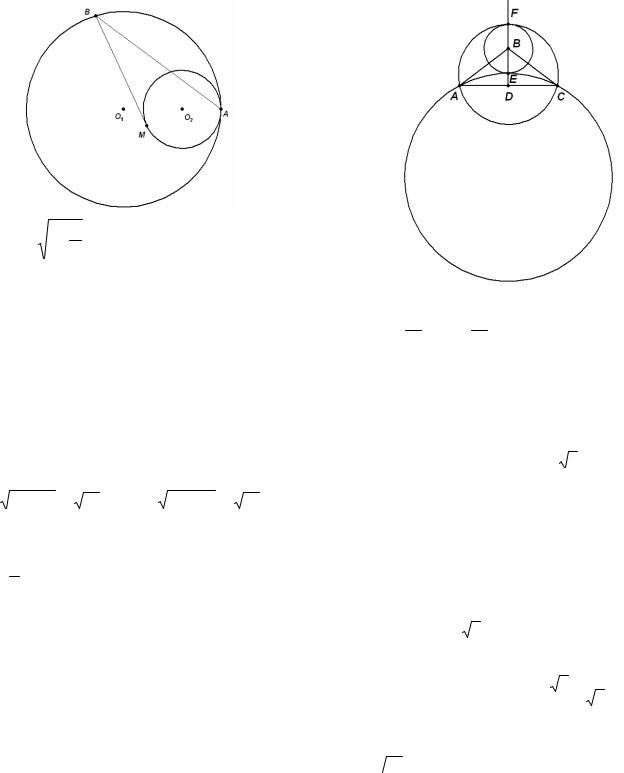
Второе решение.
Продолжим АВ до пересечения с окружностью S2 в точке Е. Треугольники AO1 B и AO2 E равнобедренные и подобные, так как
O1 AB = OA2 E .
Следовательно, AEAB = Rr и AE = arR .
По теореме о секущей и касательной имеем
BM 2 |
= BA BE , BM 2 = BA (BA + AE) , |
||||||||||
|
2 |
|
|
ar |
|
|
|
|
|||
BM |
|
= a a + |
|
|
, |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
R |
|
|
|
|
||
|
|
|
|
|
ar |
|
|
r |
|
||
BM = |
a a + |
|
|
|
|
= a |
1 + |
|
. |
||
|
|
|
R |
||||||||
|
|
|
|
|
R |
|
|
|
|||
2) Окружности касаются внутренним образом (рассмотрите самостоятельно).
12
Ответ: a 1± Rr
Пример 23. (2010) Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Решение. Пусть D – середина основания АС данного треугольника АВС. Обозначим через Е и F точки пересечения прямой BD и окружности с центром в точке В и радиусом 2. Тогда
AD = 4 , BD = 3, ED =1, FD = 5.
Из треугольников АDЕ и |
|
АDF найдем |
|
AE = 42 +12 = 17 , AF = 42 +52 = 41 со- |
|||
ответственно. Площади S AEC = |
1 |
8 1 = 4, |
|
2 |
|||
|
|
||
S AFC = 12 8 5 = 20.
1) Искомая окружность описана вокруг треугольника АЕС. Найдем ее радиус
R = |
AE EC AC |
= |
17 8 |
= |
|
17 |
. |
|
4 4 |
2 |
|||||
|
4S AEC |
|
|
||||
2) Искомая окружность описана вокруг треугольника АFС. Найдем ее радиус
R = |
AF FC AC |
= |
41 8 |
= |
|
41 |
. |
|
4 20 |
10 |
|||||
|
4S AFC |
|
|
||||
13
Ответ: 172 или 1041.
Пример 24. (2010) Дана окружность радиуса 2 с
центром О. Хорда |
АВ пересекает радиус |
ОС в |
точке D, причем |
CDA =120D . Найдите ради- |
|
ус окружности, вписанной в угол ADC |
и ка- |
|
сающейся дуги АС, если OD = 3 . |
|
|
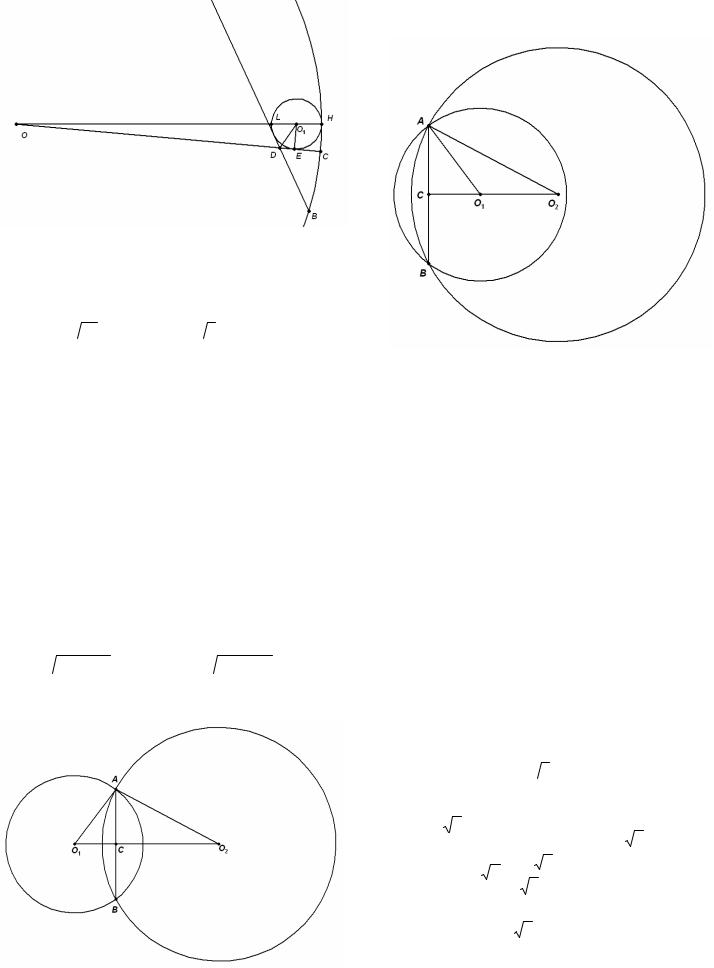
Решение. 1) Рассмотрим внутреннее касание окружностей. Пусть радиус искомой окружно-
сти с центром O1 |
равен r. Е – точка касания |
|
этой окружности |
с радиусом |
ОС. В прямо- |
угольном треугольнике EDO |
EDO = 60D |
|
|
1 |
1 |
( O1 D - биссектриса угла ADC).
DE = r ctg60D = |
r |
. |
|
3 |
|||
|
|
Используем теорему о секущей и касательной.
OL OH = OE |
2 |
, |
(2 − 2r) 2 |
|
|
r |
|
2 |
|
= |
3 + |
|
|
, |
|||
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
r 2 +18r −3 = 0.
Откуда один положительный корень r = 2 21 −9.
21 −9.
2) Центры окружностей лежат по одну сторону от хорды АВ (рассмотрите самостоятельно).
2) Случай внешнего касания окружностей рассмотрите самостоятельно. Искомая окружность касается продолжений сторон DC и DA и данной окружности.
Ответ: 2 21 −9 или 3 + 2
21 −9 или 3 + 2 3 .
3 .
Расположение центров пересекающихся окружностей относительно их общей хорды
Пример 25. (2010) Окружности радиусов 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей, если
АВ = 16.
Решение. 1) Центры окружностей лежат по разные стороны от их общей хорды АВ.
Линия центров O1O2 перпендикулярна хорде АВ и делит ее в точке пересечения С пополам. Из прямоугольных треугольников O1 AC и
O2 AC |
соответственно |
получаем |
O1C =  102 −82 = 6 и O2C =
102 −82 = 6 и O2C =  17 2 −82 =15.
17 2 −82 =15.
Искомое расстояние между центрами равно
O1O2 = O1C +O2C = 6 +15 = 21.
Ответ: 21 или 9.
Пример 26. (2010) Окружности с центрами O1 и O2 пересекаются в точках А и В. Известно,
что AO B = 90D , |
AO |
B = 60D , |
O O |
2 |
= a . |
1 |
2 |
|
1 |
|
Найдите радиусы окружностей.
• Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде и делит ее пополам. (докажите)
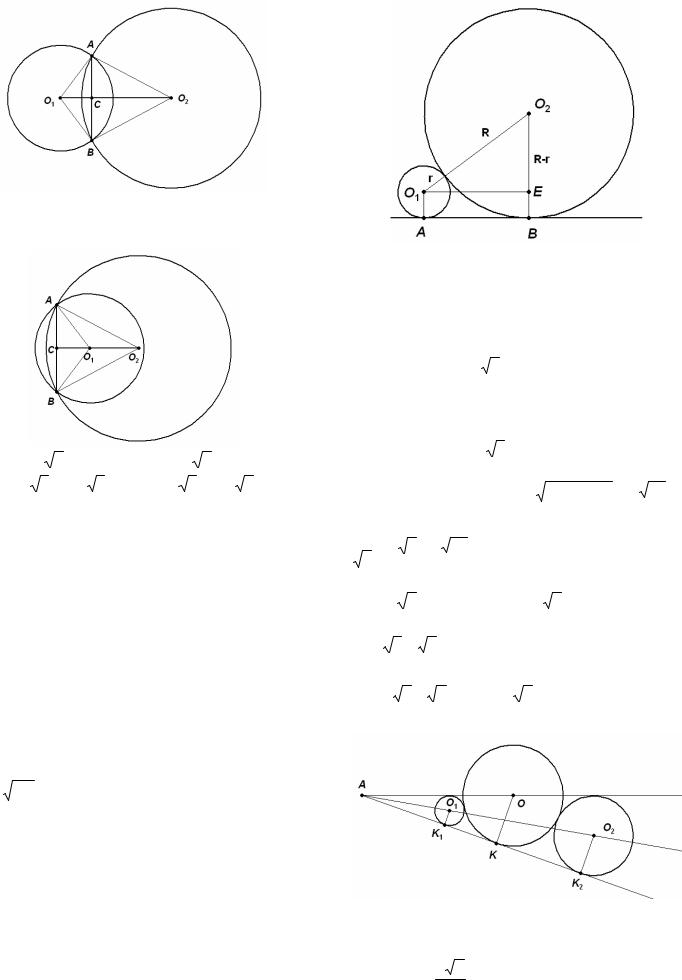
Решение. 1) Центры окружностей лежат по разные стороны от их общей хорды АВ.
Так как треугольники AO1 B и AO2 B равнобедренные, то линия центров является биссектри-
сой |
углов |
AO1 B и |
AO2 B. Имеем |
|
AO C = 45D , |
AO |
C = 30D . |
||
1 |
2 |
|
|
|
Пусть |
AC = x. Из треугольника AO1C получа- |
|||
ем AO C = CAO = 45D , |
O C = AC = x. Для |
|||
|
1 |
1 |
|
1 |
треугольника |
AO2C имеем |
|
||
O2C = AC ctg30D = x 3 .
3 .
Далее имеем |
O1O2 |
= O1C +O2C или |
|||||
a = x + x 3 . Отсюда находим x = |
a |
. |
|||||
|
|||||||
|
|
|
|
|
|
3 +1 |
|
Тогда O A = x |
2 = |
a 2 |
, |
|
|
||
|
|
|
|
||||
1 |
|
|
3 +1 |
|
|
||
|
|
|
|
|
|||
O2 A = 2 AC = 2x = |
|
2a |
. |
|
|
||
|
|
|
|
||||
|
|
|
3 +1 |
|
|
|
|
14
2) Центры окружностей лежат по одну сторону от хорды АВ (рассмотрите самостоятельно).
Ответ: |
a 2 |
|
, |
2a |
|
или |
a 2 |
|
, |
2a |
. |
3 + |
|
3 +1 |
3 −1 |
|
|||||||
|
1 |
|
|
3 −1 |
|||||||
Окружность, касающаяся одной из двух дуг другой окружности
Пример 27. (2010) Точка О – центр окружности радиуса 2. На продолжении радиуса ОМ взята точка А. Через точку А проведена прямая, касающаяся окружности в точке К. Известно, что
OAK = 60D . Найдите радиус окружности, впи-
санной в угол ОАК и касающейся данной окружности внешним образом.
Решение. Центр O1 искомой окружности лежит
на биссектрисе угла А, поэтому O AK |
1 |
= 30D . |
|||||||||
|
K1 |
|
|
|
|
|
1 |
|
|
||
|
- точка касания этой окружности с прямой |
||||||||||
АК. |
Из |
треугольника |
O1 AK1 |
|
находим |
||||||
|
AK1 = r ctg30D = r 3 , |
где |
r – радиус искомой |
||||||||
окружности. |
|
|
|
|
|
||||||
Из |
треугольника |
|
OAK |
|
находим |
||||||
|
AK |
= OK |
ctg60D = |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
Отрезок внешней касательной окружностей с |
|||||||||||
центрами О и O1 равен 2 |
OK O1 K1 |
= 2 2r . |
|||||||||
Получаем |
AK = AK1 + K1 K , |
|
|
|
|||||||
|
2 |
|
= r 3 + 2 2r . |
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Решаем квадратное уравнение |
|
|
|
||||||||
3t 2 |
+ 2 6 t − 2 = 0 , где |
t = |
r . |
|
|
|
|||||
Получаем единственный положительный корень
t = |
2 |
3 − |
6 |
. Тогда |
|
|
|||
|
3 |
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 3 − |
6 |
|
6 |
−4 2 |
|
||
r = |
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
• Отрезок общей внешней касательной к двум касающимся окружностям радиусов r и R ра-
вен 2 R r . (докажите)
Еще один случай расположения окружностей рассмотрите самостоятельно.
Ответ: 2 ± 4 32 .
15
Тематические задачи
Медианы треугольника
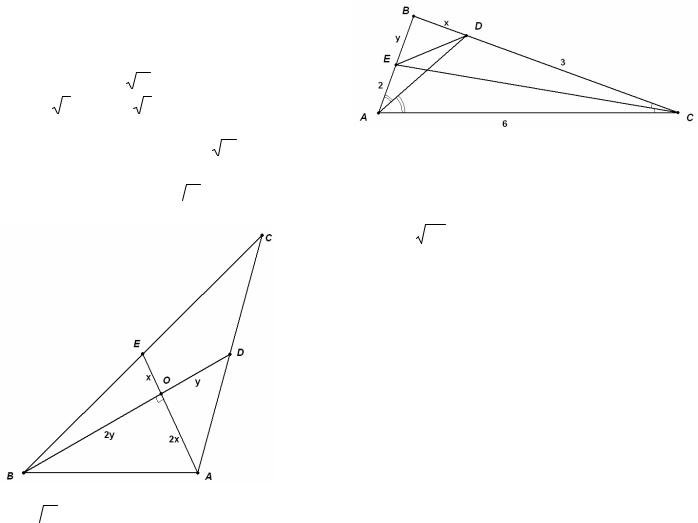
Пример 28. (2010) Найдите площадь треугольника ABC, если АС = 3, ВС = 4, а медианы, проведенные из вершин А и В, перпендикулярны.
•Каждая медиана делится точкой пересечения в отношении 2:1, считая от вершины.
•Три медианы делят треугольник на шесть равновеликих треугольников. (докажите)
Решение. Пусть медианы ВD и АE пересекаются в точке О. Обозначим ОЕ = х, OD = у. Тогда по свойству медиан треугольника АO = 2х, ВO = 2у и из прямоугольных треугольников ВOЕ и
АОD получим уравнения 4y2 + x2 = 4 и y2 +4x2 = 2,25.Решая полученную систему, по-
лучаем |
x = |
1 |
|
и |
y = |
|
11 |
. |
|
|
|
|
|
3 |
|
|
|||||
|
3 |
|
|
2 |
|
|
|
|||
Далее находим |
|
|
|
|
|
|
|
|||
|
SAOB = 0,5 2x 2y = 2xy = |
11 |
. |
|||||||
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
SABC = 3SAOB =  11.
11.
Ответ:  11.
11.
Биссектрисы треугольника
16
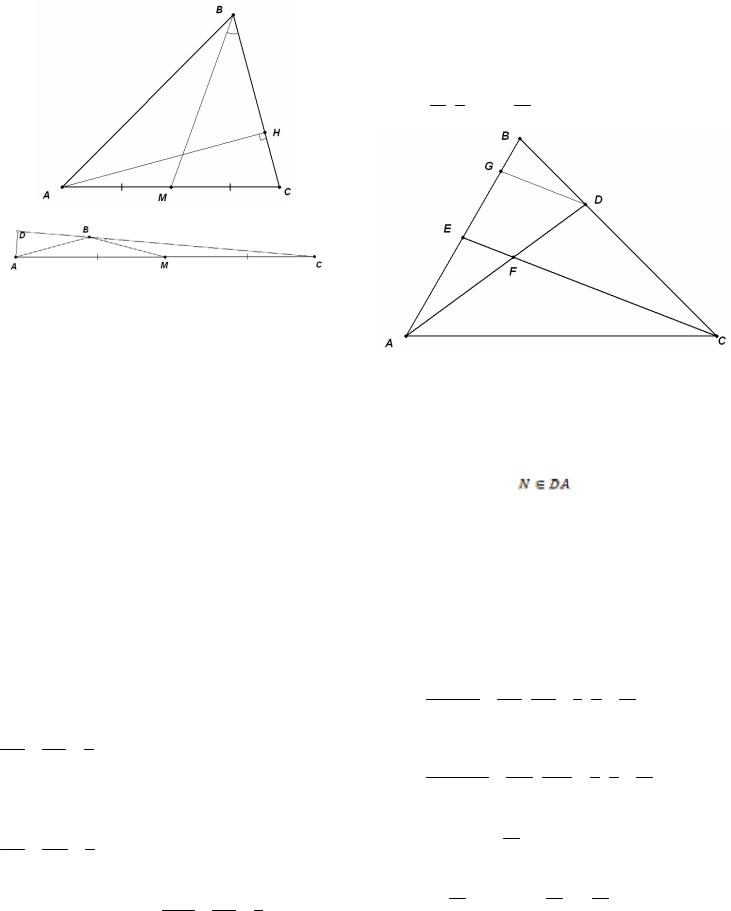
Пример 29. (2010) В треугольнике ABC проведены биссектрисы AD и СЕ. Найдите длину отрезка DE, если АС = 6, АЕ = 2, CD = 3.
• Биссектриса делит сторону треугольника на части, пропорциональные длинам прилежащих сторон.
Решение. Обозначим BD = x, BE = y. По свой-
ству |
|
биссектрисы |
получаем |
|
BD |
= |
AB |
и |
|||||||
|
|
DC |
AC |
||||||||||||
AE |
|
AC |
|
x |
|
y +2 |
|
|
|
|
|
|
|||
= |
или |
= |
и |
2 |
|
= |
6 |
. |
|
|
|
||||
BE |
BC |
3 |
6 |
y |
x +3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
Из решения системы
6x =3y +62x +6 =6y
находим х = 1,8 и у = 1,6. Тогда ВС = 4,8 и
АВ = 3,6.
Так как 3,62 +4,82 = 62 , то по теореме, обратной теореме Пифагора, имеем B =90D .
Тогда ED2 = x2 + y2 =1,62 +1,82 =5,8.
Ответ: 5,8.
Метод площадей
Пример 30. (2010) Медиана ВМ треугольника АВС равна его высоте АН. Найдите угол МВС. Решение. Пусть MBC =α. Найдем площадь
треугольника АВС двумя способами. Так как медиана ВМ треугольника АВС разбивает его на два равновеликих треугольника, то
SABC = 2SCBM = 2 |
1 |
|
BC BM sinα = BC BM sinα. |
||
|
|||||
2 |
|
|
|
|
|
С другой стороны, |
SABC = 0,5BC AH . |
Учиты- |
|||
вая, что AH = BM , приравняем |
площади |
||||
BC BM sinα = 0,5BC AH . |
Получаем, что |
||||
sinα = 0,5. Отсюда α = 30D |
или α =150D . |
||||
Для треугольников AFE и ADG, имеющих общий угол, получаем
SAFE |
= |
AE AF |
= |
AE |
|
AF |
= |
1 |
|
3 |
= |
|
3 |
. |
|
SADG |
AB AD |
AB |
AD |
2 |
5 |
10 |
|||||||||
|
|
|
|
|
|
|
|||||||||
SAFE = 103 13 SABC = 101 SABC .
Ответ: 30D или 150 D .
Отношение отрезков и площадей
Пример 31. (2010) В треугольнике ABC на стороне ВС выбрана точка D так, что BD : DC =1: 2 . Медиана СЕ пересекает отрезок AD в точке F. Какую часть площади треугольника АВС составляет площадь треугольника
AEF?
•Медиана делит треугольник на два равновеликих треугольника. (докажите)
•Параллельные прямые отсекают на сторонах угла (на двух прямых) пропорциональные отрезки (обобщенная теорема Фалеса).
Решение. Возьмем точку G на АВ так, что
DG || EC. Пусть BG = x.
В треугольнике ВСЕ используем теорему Фалеса:
EGBG = CDDB = 12 . Тогда EG = 2x, и AE = EB = 3x.
В треугольнике ADG используем теорему Фалеса:
ADAF = AGAE = 53 .
Для треугольников ABD и ACD, имеющих об-
щую высоту, получаем SABD = BD = 1
SABC BC 3
и |
SABD = |
1 |
|
SABC . |
|
3 |
|||||
|
|
|
|||
17
Ответ: 0,1.
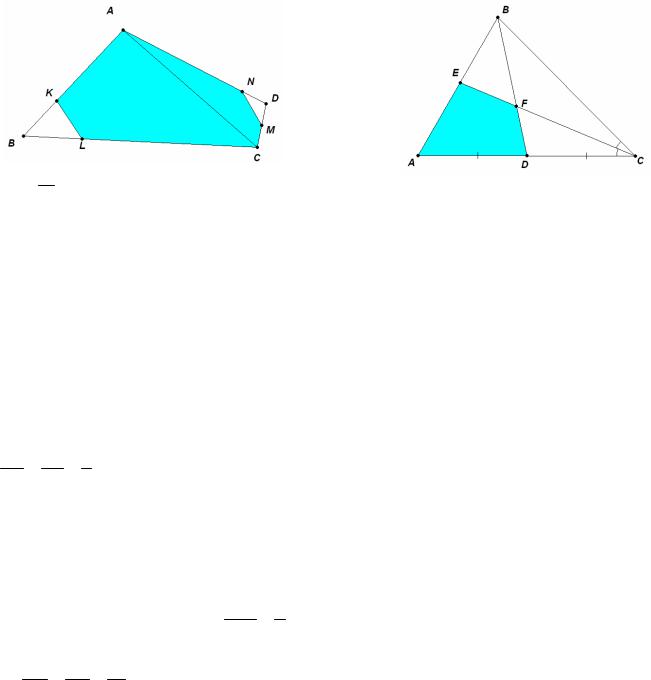
Пример 32. (2010) На сторонах выпуклого че-
тырехугольника ABCD, |
площадь которого рав- |
||||||||||||
на |
единице, взяты |
точки |
K AB , |
L BC , |
|||||||||
|
M CD и N DA |
|
|
. При этом |
AK |
= 2, |
|||||||
|
|
||||||||||||
|
BL |
|
1 |
|
CM |
|
DN |
|
1 |
|
|
KB |
|
|
= |
, |
=1, |
= |
|
. Найдите площадь |
|||||||
|
LC |
|
|
NA |
|
||||||||
|
3 |
MD |
3 |
|
|
|
|||||||
шестиугольника AKLCMN.
• Отношение площадей треугольников, имеющих общий угол, равно отношению произведению сторон этого угла. (докажите)
Решение. Отношение площадей треугольников
KBL и АВС
равно BKAB BCBL = BKAB BCBL = 13 14 = 121 .
Отношение площадей треугольников MND и
АDС
равно
Значит, сумма площадей треугольников KBL и MND составляет 121 от площади данного четы-
рехугольника, а площадь шестиугольника составляет 1211 т.е. равна 1211 1 = 1211.
Ответ: 1211 .
Пример 33. (2010) В треугольнике ABC, площадь которого равна S, биссектриса СЕ и медиана BD пересекаются в точке F. Найдите площадь четырехугольника ADFЕ, если ВС = а,
АС = b.
•Медиана делит треугольник на два равновеликих треугольника. (докажите)
•Если у двух треугольников равны высоты, то их площади относятся как основания. (докажи-
те)
Решение. 1) По свойству биссектрисы СЕ име-
ем BEAE = CBCA = ba . Тогда для треугольников АСЕ
и АВС с общей высотой (можно провести из
вершины С) |
получаем |
SAEC |
= |
AE |
= |
b |
. |
От- |
||
SABC |
AB |
a +b |
||||||||
|
bS |
|
|
|
|
|
||||
сюда SAEC = |
. |
|
|
|
|
|
|
|
||
a +b |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
2)Так как BD – медиана, то SBDC = SABC2 = S2 .
3)CF – биссектриса в треугольнике BDC, по-
DF = CD = b
этому FB DB 2a .
Для треугольников CDF и ВСD с общей высотой (можно провести из вершины С) получаем
|
SCDF |
= |
DF |
= |
|
b |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
SBDC |
DB |
2a +b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда SCDF |
= |
|
|
b |
|
SBDC = |
|
|
|
bS |
|
. |
|
|
|||||||||||
2a +b |
|
2(2a +b) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4) Теперь SADFE = SAEC −SCDF |
|
= |
|
|
|
|
|
|
|||||||||||||||||
|
|
bS |
|
|
bS |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
|
− |
|
|
|
|
|
= bS |
|
|
− |
|
|
|
|
|
|
=. |
|||||
a +b |
2(2a +b) |
|
|
2(2a |
+b) |
||||||||||||||||||||
|
|
|
|
|
a +b |
|
|
|
|
|
|||||||||||||||
= |
|
Sb(3a +b) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2(a +b)(2a +b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: |
Sb(3a +b) |
. |
|
2(a +b)(2a +b) |
|||
|
|
Метод вспомогательной окружности
Пример 34. (2010) Дан прямоугольный треугольник АВС с прямым углом при вершине В и углом α при вершине А. Точка D - середина гипотенузы. Точка С1 симметрична точке С относительно прямой BD. Найдите угол AC1 B .
• Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Решение. Так как прямая BD является серединным перпендикуляром к отрезку CC1 , то
DC = DC1 . С другой стороны, точка D – центр окружности, описанной около прямоугольного
треугольника. Поэтому |
DC = DB = DA . Отсю- |
|
да следует, что точка C1 принадлежит описан- |
||
ной окружности. |
|
|
1) Если α = 45D , то |
центральный |
угол |
BDC = 2 BAC = 90D . В этом случае ось BD |
||
перпендикулярна гипотенузе АС. Точка |
С ото- |
|
бразится в точку А, и угол AC1 B не будет определен.
18
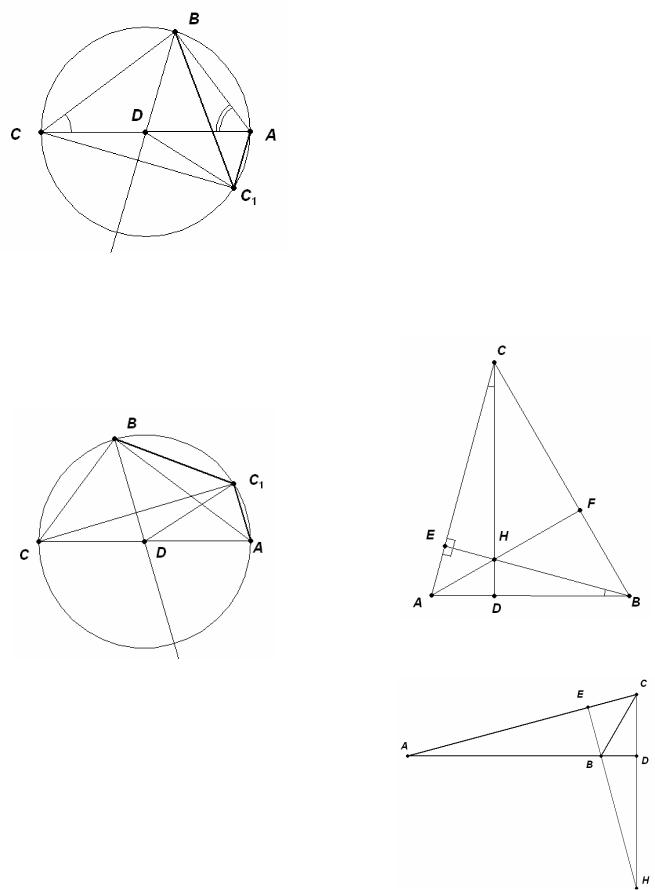
2) Пусть α > 45D , тогда |
центральный |
угол |
BDC = 2α > 90D . В этом случае точки С и C |
||
|
|
1 |
расположены по одну сторону от хорды |
АВ. В |
|
прямоугольном треугольнике |
BCA = 90D |
−α. |
Вписанные углы, опирающиеся на одну и ту же дугу, равны. Поэтому
AC1 B = BCA = 90D −α.
• (Признак равенства прямоугольных треугольников) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Решение. 1) Треугольник АВС - остроугольный. Пусть ВЕ и CD – высоты треугольника. Углы АВЕ и HCE равны, как углы с соответственно перпендикулярными сторонами. Треугольники
АВЕ и |
HCE равны по гипотенузе (СН = АВ) и |
|
острому |
углу. Отсюда |
AE = EH , и значит, |
EAH = AHE = 45D . |
В прямоугольном тре- |
|
угольнике ACF имеем |
CAF = 45D , |
|
поэтому |
ACF = 45D . |
|
3) Пусть α < 45D , тогда центральный уголBDC < 90D . В этом случае точки С и C1 расположены по разные стороны от хорды АВ. Четырехугольник AC1 BC вписан в окружность, поэтому
AC1 B =180D − BCA =180D −(90D −α) = 90D +α. Ответ: 90D +α, если 0D <α < 45D ; 90D +α,
если 45D <α < 90D ; при α = 45D точка С1 совпадает с точкой А и угол не определен.
Высоты треугольника
Пример 35. (2010) Высоты треугольника ABC пересекаются в точке Н. Известно, что СН = АВ. Найдите угол АСВ.
19
Остальные случаи рассмотрите самостоятельно. 2) Угол АВС – тупой.
3) Угол ВАС – тупой.
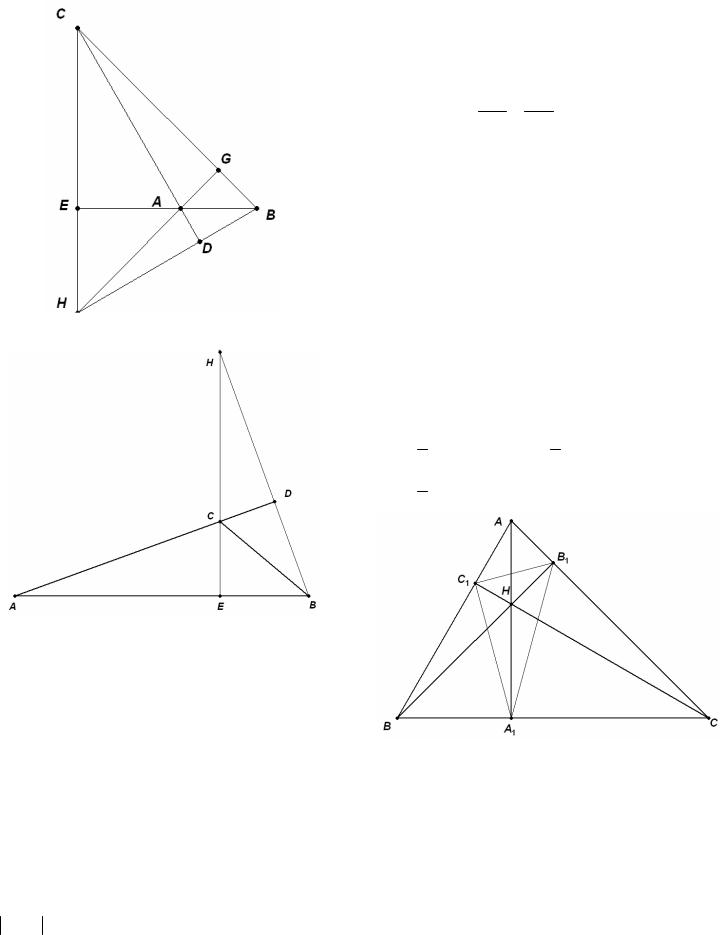
4) Угол АСВ – тупой.
5)Угол АВС – прямой.
6)Угол ВАС – прямой.
7)Случай, когда угол АСВ – прямой, невозможен (почему?).
Ответ: 45D или 135D .
BA1 |
= cos B |
и |
BC1 |
= cos B соответственно. |
|
AB |
BC |
||||
|
|
|
Следовательно треугольники BA1C1 и BAC подобны (второй признак), так как имеют об-
щий угол В и BAAB1 = BCBC1 = cos B.
Случай тупого угла В рассмотрите самостоятельно.
Решение. 1) Треугольник АВС – остроугольный.
Так как треугольник |
|
BC1 A 1 подобен треуголь- |
|||||||||
нику АВС, |
то BC1 A 1= BCA. Аналогично из |
||||||||||
подобия треугольников |
A B1C1 и АВС |
имеем |
|||||||||
AC1 B 1= BCA. Далее |
развернутый угол при |
||||||||||
вершине C1 |
составлен из суммы углов |
BC1 A 1 , |
|||||||||
AC1 B1 и B1C1 A 1 . Отсюда получаем соотноше- |
|||||||||||
ние |
|
2 C + B C A |
1 |
=180D |
или |
||||||
|
1 |
|
|
|
|
1 |
1 |
|
|
||
C = 90D − |
B C A |
1 |
. |
Такие же равенства |
|||||||
|
|||||||||||
|
2 |
1 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
можно получить для других острых углов. Используем данные углы:
90D − 12 90D = 45D , 90D − 12 60D = 60D , 90D − 12 30D = 75D .
Пример 36. (2010) Точки |
A 1 , B 1 , C 1 — осно- |
Остальные случаи рассмотрите самостоятельно. |
вания высот треугольника |
ABC. Углы треуголь- |
2) Угол АСВ – тупой. |
ника A 1 B1C1 равны 90°, 60° и 30°. Найдите углы треугольника ABC.
• Пусть в треугольнике АВС проведены высоты AA1 и CC1 . Тогда треугольник A1 BC1 подобен данному с коэффициентом подобия, равным cos B .
Рассмотрим остроугольный треугольник (см. ниже рисунок). Для прямоугольных треугольников BA1 A и BC1C имеем
20
Треугольники EDB и CAB подобны (по двум углам) с коэффициентом
DEAC = BCBE = cosα,
т.е. cosα = k . Тогда по теореме косинусов
AC2 = AB2 + BC2 −2AB BC cosα = = b2 +a2 −2abk .
3)Угол АВС – тупой.
4)Угол ВАС – тупой.
Случаи, когда один из углов АВС, ВАС, АСВ – прямой, невозможны (почему?).
Замечание. Другое решение может быть основано на следующей ключевой (базовой, опорной) задаче:
• Высоты остроугольного треугольника являются биссектрисами его ортотреугольника (треугольник, образованный основаниями вы-
сот). (докажите)
Ответ: |
или |
|
|
или |
|
|
или |
|
|
. |
|
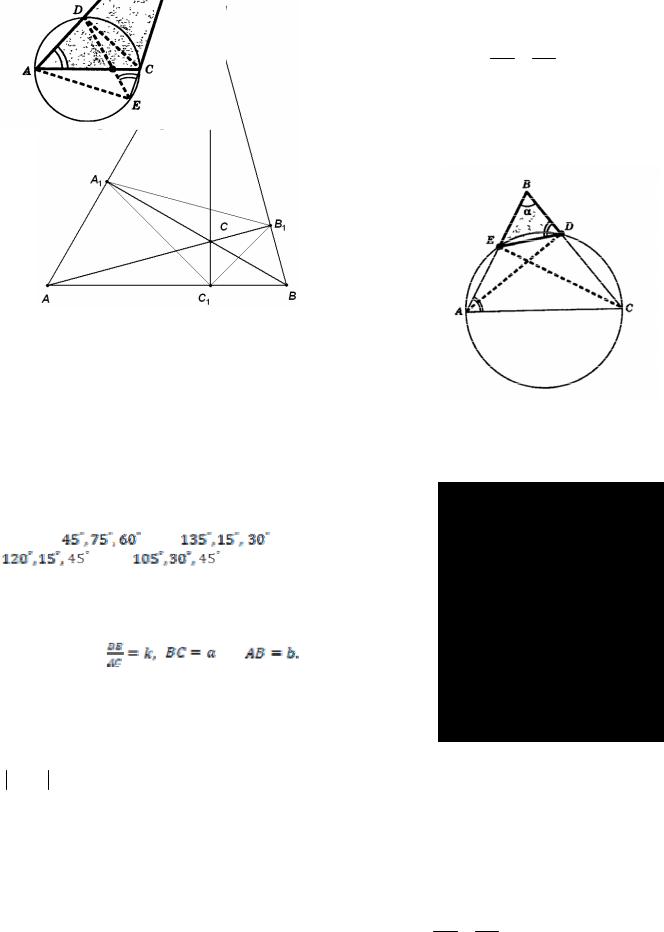
Пример 37. (2010) Точки |
D и |
E – основания |
|||
высот непрямоугольного |
треугольника |
АВС, |
|||
проведенных из вершин |
А и С соответственно. |
||||
Известно, что |
|
|
и |
Най- |
|
дите сторону АС. |
|
|
|
|
|
• Пусть в треугольнике |
АВС |
проведены высо- |
|||
ты AA1 и |
CC1 . Тогда треугольник A1 BC1 |
подо- |
|||
бен данному с коэффициентом подобия, равным cos B . (докажите)
Решение. Из точек D и Е сторона АС видна под прямым углом, значит, эти точки лежат на окружности с диаметром АС. Обозначим
ABC =α.
1)Если треугольник АВС остроугольный, то основания высот АD и СЕ лежат на сторонах треугольника. Тогда четырехугольник AEDC - вписанный, поэтому
BDE =180D − CDE = CAE = CAB.
21
2) Пусть АСВ – тупой угол.
Тогда четырехугольник AECD вписанный, и аналогично предыдущему получаем: cosα = k
и AC2 = b2 +a2 −2abk .
3)Пусть САВ – тупой угол. Аналогичные рассуждения.
4)Пусть АВС – тупой угол. Тогда основания высот АD и СЕ лежат на продолжениях сторон ВС и АВ. Вписанные углы CDE и CAE опираются на одну и ту же дугу, поэтому
BDE = CDE = CAE = CAB.
Треугольники EDB и CAB подобны (по двум углам) с коэффициентом
DEAC = BDAB = cos(180D −α) = −cosα, т.е. cosα = k .
Тогда AC2 = a2 +b2 +2abk .
