5. Однофакторный дисперсионный анализ

5.1. Основные понятия

Пусть результаты наблюдений составляют l независимых выборок (групп), полученных из l нормально распределенных генеральных совокупностей, которые имеют, вообще говоря, различные средние m1, m2 , ..., ml и равные дисперсии D.

Проверяется гипотеза о равенстве

средних H0 : m1, = m2 , = ... = ml .

На практике такая задача возникает при исследовании влияния, которое оказывает изменение некоторого фактора на измеряемую величину. Например, если измерения проводятся на l различных приборах, то можно исследовать влияние фактора "прибор" на результаты измерения. Суть однофакторного дисперсионного анализа состоит в следующем.

n - общее число наблюдений,

l

n = ånk . k=1

141

Общая сумма квадратов отклонений наблюдений от общего среднего x может быть представлена так:

Это основное тождество дисперсионного анализа. Запишем его в виде

Q = Q1 + Q2,

где Q - общая сумма квадратов отклонений наблюдений от общего среднего; Q1 - сумма квадратов отклонений выборочных средних групп от общего среднего (между группами); Q2 - сумма квадратов отклонений наблюдений от выборочных средних групп (внутри групп).

Основное тождество легко проверяется, если

åå(xik − x) (xk − x) = 0 k =1 i=1

в силу определения средних xk и x .

Если верна гипотеза H0 о равенстве средних, то можно показать, что статистики Q1/D и Q2/D независимы и имеют распределение χ2 соответственно с l – 1 и n – l степенями свободы (см. например [22]). Следовательно, статистики

142

характеризует рассеяние групповых средних, а оценка S22 - рассеяние внутри групп, которое обусловлено случайными вариациями результатов наблюдений. Значительное превышение величины S12 над величиной S22 можно объяснить различием средних в группах.

Отношение этих оценок при условии, что верна гипотеза H0, имеет распределение Фишера с l – 1 и n – l степенями свободы.

Эта статистика используется для проверки гипотезы H0 о равенстве средних H0 : m1 = m2 = ... = ml . Гипотеза H0

не противоречит результатам наблюдений, если выборочное значение Fb статистики F меньше квантили распределения Фишера F1 – α(l – 1, n – l). Если Fb больше F1 – α(l – 1, n – l), то гипотеза H0 отклоняется и следует считать, что среди средних m1, m2, …, ml имеется хотя бы два, не равных друг другу.

Пример 5.1. Три группы водителей обучались по разным методикам. По окончании обучения было проведено контрольное тестирование произвольно отобранных водителей из каждой группы. Получены следующие результаты:

143

об отсутствии влияния разных методик обучения на результаты контрольного тестирования водителей. Предполагается, что выборки получены из независимых нормально распределенных совокупностей с одной и той же дисперсией.

Очевидно, задача заключается в проверке гипотезы H0: m1 = m2 = m3, где mk - математическое ожидание числа ошибок для водителей k-й группы. В нашем случае l = 3, n = 15.

Вычисления удобно проводить в следующей последовательности.

Сумма всех элементов xik , i = 1, 2,...,nk , k = 1, 2, ..., l трех выборок равна

lnk

x= ååxik = 10 +12 +12 = 34 ,

k =1 i=1

а сумма квадратов этих элементов равна

144

Из таблицы квантилей распределения Фишера находим

F0,95(2,12) = 3,89. Так как Fb = 6,52 > 3,89, то на уровне значимости

α = 0,05 гипотеза о равенстве средних отклоняется: разные методики обучения дают значимо различные результаты контрольного тестирования групп водителей.

Если гипотеза H0 о равенстве средних отклоняется, то требуется определить, какие именно группы водителей имеют значимое различие средних. Для этой цели используется метод линейных контрастов.

Линейный контраст Lk определяется как линейная комбинация

l

Lk = åck mk , k =1

где ck, k = 1, 2, …, l - константы, однозначно определяемые из формулировки проверяемых гипотез,

l

причем åck = 0 .

k=1

Оценка линейного контраста Lk равна

l

Lk% = åck xk ,

k=1

аоценка дисперсии линейного контраста Lk% равна

145

где SLk - оценка среднего квадратического отклонения

линейного контраста, SLk = 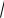D%[Lk] .

Пример 5.2. В условиях примера 5.1 при

H0(4) : 12 (m1 + m3) = m2 .

В соответствии с проверяемыми гипотезами H0(1) , i =

1, 2, 3, 4,

определяются линейные контрасты:

Lk1 = m1 – m2; c1 = 1, c2 = –1, c3 = 0; Lk2 = m1 – m3; c1 = 1, c2 = 0, c3 = –1; Lk3 = m2 – m3; c1 = 0, c2 = 1, c3 = –1;

Lk4 = 1/2(m1 + m2) – m3; c1 = 1/2, c2 = 1/2, c3 = –1.

Найдем границы доверительных интервалов для линейных контрастов Lki, i = 1, 2, 3, 4.

Предварительно вычислим оценки линейных контрастов и их дисперсий. Выборочные средние по

S22 = nQ-2l = 1512,91- 3 » 1,08 .

Оценки контрастов и их дисперсий:

146