4

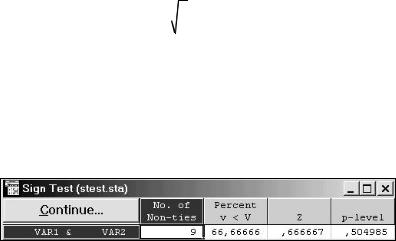
Вычисленный уровень значимости р = 0,504985 достаточно высок и больше заданного уровня значимости α = 0,10 , следовательно, гипотеза H0 не отклоняется. Следует считать, что различие в показаниях приборов вызвано случайными ошибками.

В пакете STATISTICA решение выглядит, как на рис.4.9.

Рис.4.9. Результаты решения примера 4.10

4.9. Критерий Вилкоксона (Wilcoxon watched pairs test)

Критерий Вилкоксона, так же как и критерий знаков, используется для проверки гипотезы H0 об однородности двух генеральных совокупностей по попарно связанным выборкам. Отличие состоит в том, что используется информация об относительных размерах разностей элементов двух выборок.

Проверка по критерию осуществляется следующим образом. Абсолютные значения ненулевых разностей упорядочиваются по возрастанию и определяются их ранги. Равным разностям присваивается средний ранг. Далее вычисляются суммы рангов для отрицательных

129

разностей Rn и положительных разностей Rp. Для проверки расчетов используется тождество

Статистикой критерия T является число, равное наименьшему значению суммы рангов Rn и Rp. Критические значения Т определяются по таблице ([14], с. 289, табл.67). При n > 25 используют статистику Z:

При условии, что гипотеза H0 верна, Z имеет (приближенно) стандартное нормальное распределение N(0,1). Гипотеза H0 отклоняется на уровне значимости α (при двухсторонней альтернативе), если zв > u1−α2 , где zв -

выборочное значение статистики Z, а u1−α2 - квантиль стандартного нормального распределения N(0,1) порядка 1− α2 .

Пример 4.11. Проверим гипотезу H0 об однородности генеральных совокупностей по данным в примере 4.10, используя критерий Вилкоксона.

Решение. Значения разностей v1 − v2 следующие: –2,

–1, 1, –1, 2, 0, –3, 5, –1, –2.

Упорядочим абсолютные значения ненулевых разностей, отметим их знак и определим ранги (нулевая разность не учитывается):

130

Сумма рангов отрицательных разностей Rn = 27,5, сумма рангов положительных разностей Rp = 17,5, таким образом, статистика критерия T = 17,5. По таблице ([14], табл.67) критическое значение Tкр для n = 9 на 5%-ном уровне значимости для двустороннего критерия равно 5; так как Т > 5, то гипотеза H0 принимается.

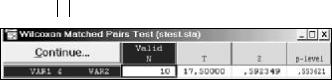
В пакете STATISTICA выводятся следующие результаты процедуры Wilcoxon watched pairs test (рис.4.10):

значение Т-статистики = 17,5; значение Z-статистики ≈ 0,592;

p − level = P[ Z > 0,592] ≈ 0,553.

Рис.4.10. Результаты решения примера 4.11

Задания для самостоятельной работы

Решите задачи, используя критерий знаков и критерий Вилкоксона. Сравните и прокомментируйте результаты.

1. Сравнивалось действие двух экстрактов вируса табачной мозаики. Для этого каждая из двух половин листа натиралась соответствующим препаратом. Число пораженных мест приводится ниже:

131

Можно ли считать, что действие экстрактов различно? Принять α = 0,01.

2. Ниже приводится время решения (в секундах) контрольных задач одиннадцатью учащимися до и после специальных упражнений по устному счету:

Можно ли считать, что эти упражнения улучшили способности учащихся в решении задач? Принять α = 0,01.

3. Для десяти человек была предложена специальная диета. После двухнедельного питания по этой диете масса их тела изменилась следующим образом:

Можно ли рекомендовать эту диету для людей, желающих похудеть?

Оказывает ли эта диета какое-либо существенное действие на массу тела? Принять α = 0,10.

4. Проверить предположение о том, что предлагаемый лечебный препарат не меняет состав крови (в частности, число лейкоцитов), если препарат испытывался на десяти особях, а последующий анализ крови дал следующие результаты:

0,97; 1,05; 1,09; 0,88; 1,01; 1,14; 1,03; 1,07; 0,94; 1,02 (числа выражают отношение числа лейкоцитов в опыте к числу лейкоцитов в норме). Принять α = 0,01.

132

5. Изучалось влияние черного и апрельского пара на урожай ржи. Опыт длился 6 лет. Учитывалась масса 1000 зерен (в граммах). Результаты опыта следующие:

Можно ли считать, что урожай ржи, посеянной по апрельскому пару, значимо выше? Проверить это предположение, если α = 0,05.

6. Изменение урожайности при применении одного из видов предпосевной обработки семян характеризуется следующими данными (ц/га):

Можно ли считать, что предпосевная обработка семян увеличивает урожайность? Принять α = 0,05.

4.10.Однофакторный анализ Фридмана

икоэффициент конкордации Кендалла

(Friedman ANOVA and Kendall’s concordance)

Рассмотрим следующую задачу. Кинопленка четырех видов была представлена трем экспертам для определения лучшей. Каждому эксперту предложили упорядочить пленки по степени предпочтения. Баллы (ранги), проставленные экспертами, приведены в таблице. Наибольший балл соответствует пленке самого лучшего качества.

133

Требуется определить, различаются ли виды пленок и согласованы ли оценки экспертов. Если оценки экспертов не согласованы, т.е. являются независимыми, то такими оценкам, очевидно, нельзя доверять, так как в этом случае оценки носят случайный характер и на них не оказывают влияния представленные пленки.

Эту задачу можно обобщить.

Пусть таблица результатов оценки или наблюдений n объектов состоит из k строк и n столбцов. В строках записываются k ранжированных переменных, причем длины ранжировок (объемы выборки) равны n. Строки таблицы можно рассматривать как k связанных выборок объемом n. Связность выборок следует из того, что выборки - суть повторные наблюдения на одних и тех же n объектах. Если объекты не различаются между собой, суммы рангов по столбцам также не будут различаться. Нулевая гипотеза H0: между столбцами нет различия - проверяется с помощью статистики Фридмана F.

Выборное значение F-статистики Fв вычисляется по формуле

134

c2−α (n -1) -го порядка (1- a).

1

Мерой согласия различных ранжировок n объектов является коэффициент конкордации (согласия) Кендалла:

ранжировок совпадают. Статистическая значимость W проверяется на основе того, что статистика k(n -1)W при

k ® ¥ имеет (приближенно) распределение хи-квадрат с (n -1) степенями свободы. Если n ≤ 7, то для проверки

статистической значимости W используют таблицы критических значений (см. [21], табл.П16б).

В случае, когда в ранжировках (в строках таблицы)

135

групп повторяющихся рангов в i-й ранжировке; nt - число совпадающих рангов в группе с номером t, i = 1, 2, ..., m.

Пример 4.12. Вычислим статистику Фридмана F и коэффициент конкордации W по данным задачи об экспертах кинопленки.

Решение. В этом примере число ранжировок k = 3, объем выборки n = 4. Суммы рангов по столбцам: 6, 3, 11, 10. Значение выборочной статистики критерия равно

Fв = 3×4 ×12(4 +1) (62 + 32 +112 +102 )-3×3×(4 +1) = 8,2 ,

при α = 0,05, c0,952 (3) = 7,81 , следовательно, на уровне

значимости

α = 0,05 гипотеза H0 отклоняется: следует считать, что виды пленок, по мнению экспертов, различны.

Коэффициент конкордации равен

W = 3(48,2-1) = 8,29 = 0,91.

Большое значение W свидетельствует о согласованности оценок экспертов.

При решении задачи в модуле Non. parametrics пакета STATISTICA данные вводятся как n переменных (vars), каждая из которых имеет k значений (cases). Данные можно вводить в виде любых чисел, ранжировка производится при вычислениях.

Таблица результатов содержит по каждой переменной (столбцу): средний ранг, сумму рангов, среднее и стандартное отклонение; выборочное значение статистики Фридмана Fв, уровень значимости

136

среднее значение рангового коэффициента корреляции Спирмена rs вычисленный как среднее по всем

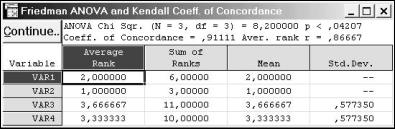
В пакете STATISTICA выводятся результаты, представленные на рис.4.11.

Рис.4.11. Результаты решения примера 4.12

4.11. Q-критерий Кокрена (Cochran Q- test)

Критерий применяется в следующей ситуации. Предположим, что n объектов подвергается k различным воздействиям или условиям. Результаты записываются в виде "да - нет", "1" - "0", "+" - "–" и так далее.

Для примера рассмотрим такую задачу. Во время презентации четырех новых сортов

мороженого пятнадцати покупателям было предложено попробовать все сорта мороженого и высказать свое отношение к каждому сорту в следующем виде: 0 - нравится,

137

1 - не нравится. Ответы покупателей приведены в следующей таблице:

Требуется проверить гипотезу H0: все сорта мороженого нравятся покупателям в равной степени. Альтернативная гипотеза H1 утверждает, что сорта мороженого нравятся покупателям в разной степени. Для проверки гипотезы H0 используется критерий Кокрена. Статистика критерия Q вычисляется следующим образом:

1)найдем число единиц в каждом столбце u1, u2, ..., uk и число единиц в каждой строке v1, v2, ..., vn;

2)вычислим следующие суммы и суммы квадратов:

3). вычислим статистику критерия Q по формуле

138

При условии, что гипотеза H0 верна, распределение статистики Q сходится при n → ∞ к распределению хи-

квадрат с (k -1) степенями свободы. Таким образом,

гипотеза H0 отклоняется на уровне значимости α, если

Q> c2−α (k -1),

в1

где c12−α (k -1) - квантиль распределения c2 (k -1) -го порядка (1- a) , а Qв - выборочные значения статистики

Q.

Пример 4.13. Проверить гипотезу H0 по данным в приведенной выше таблице.

Решение. Вычислим суммы по столбцам и строкам таблицы: результаты приведены в исходной таблице.

Далее вычислим:

4

åui = 11+ 8 + 4 + 7 = 30; i=1

Выборочное значение статистики Q равно

139

Так как c0,952 (3) = 7,81 , что больше Qв, то на уровне значимости

α = 0,05 гипотеза H0 не отклоняется: следует считать, что все сорта мороженого нравятся покупателям в равной степени.

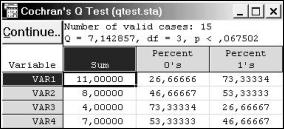
При решении задачи в опции Cochran Q-test данные вводятся как k переменных (vars), каждая из которых имеет n значений (cases), записанных как 0 и 1, либо двумя другими кодами, значение которых надо установить перед выполнением процедуры. Таблица результатов, показанная на рис.4.12, содержит: суммы для каждой переменной, проценты нулей и единиц, выборочное значение статистики Q, число степеней свободы статистики хи-квадрат df = k – 1 и уровень

значимости: p = P[c2 (k -1) > Qв ].

Рис.4.12. Результаты решения примера 4.13

140