
- •Введение
- •Глава 1. Cлучайные события
- •§ 1. Предмет теории вероятностей
- •§ 2. Пространство элементарных событий
- •§ 3. Классическое определение вероятности
- •§ 4. Некоторые комбинаторные формулы
- •§ 5. Геометрические вероятности
- •§ 6. Аксиоматическое построение теории вероятностей
- •§ 7. Условные вероятности
- •§ 8. Вероятность суммы и произведения событий
- •§ 9. Зависимые и независимые события
- •§ 10. Формула полной вероятности
- •§ 11. Формула Байеса
- •Глава 2. Случайные величины
- •§ 1. Дискретные случайные величины
- •§ 2. Функция распределения случайной величины
- •§ 3. Числовые характеристики дискретных случайных величин
- •§ 4. Моменты
- •§ 5. Производящая функция
- •§ 6. Биномиальное распределение
- •§ 7. Распределение Пуассона
- •§ 8. Геометрическое распределение
- •§ 9. Непрерывные случайные величины
- •§ 10. Характеристики непрерывных случайных величин
- •§ 11. Примеры непрерывных случайных величин
- •§ 12. Функция распределения нормального закона
- •Глава 3. Cиcтемы случайных величин
- •§ 1. Распределение системы случайных величин
- •§ 3. Нормальное распределение на плоскости
- •§ 4. Зависимость и ковариация
- •§ 5. Kоэффициент корреляции и его свойства
- •Глава 4. Некоторые предельные теоремы
- •§ 1. Центральная предельная теорема
- •§ 2. Закон больших чисел
- •Литература
Ecли рассмотреть сочетания без повторения из n + m – 1-го элемента по m, то их столько же: на j позиций выбираются элементы из n, а на (m – j) позиций - из (m – 1):
m
Cm+ − = ∑C jCm− j . n m 1 n m−1
j =1
Поэтому Čmn = Cnm+m−1 . ♣
Пример 3. Рассмотрим игру в преферанс, когда старшие 32 карты колоды сдаются по 10 трем игрокам, а 2 карты кладутся в "прикуп". Какова вероятность, что в прикупе окажутся два туза?
Число различных комбинаций из двух карт, которые могут оказаться в прикупе, равно числу сочетаний C322 = 32!/(2! 30!) = 496.
Эти сочетания и образуют пространство элементарных событий Ω. В карточной колоде 4 туза. Число элементарных событий, дающих два
туза, равно числу сочетаний C42 =4!/(2! 2!)=6. Вероятность двух тузов в прикупе Р(А) = 6/496 = 0,012…♦
Лекция 2
§ 5. Геометрические вероятности
Cогласно классическому определению, в опытах с конечным числом равновозможных исходов вероятность события А - это доля исходов, которые приводят к наступлению события А в общем количестве
|
|
|
|
1,5 мин |
исходов. |
Определять |
вероятность |
|
A |
C |
как долю благоприятных исходов |
||||||
B |
||||||||
|
|
|
|
|
можно и в опытах с бесконечным |
|||
|
|
|
|
|
||||
|
|
4 мин |
|
|||||
|
|
|
числом |
исходов. |
Рассмотрим |
|||
|
|
Рис.1. |
|
|||||
|
|
|
примеры |
подсчета так |
называемых |
|||
"геометрических" вероятностей. Пример 4. Поезда в метро отправляются со станции с интервалом
в 4 мин. Какова вероятность, что пассажир, пришедший на платформу, отправится с нее не позже, чем через 1,5 мин?
Пространство элементарных исходов состоит из бесконечного множества точек отрезка [А,В] (рис.1), так как пассажир может
появиться на платформе в любой момент между отправлениями |
|||||||||||||
поездов. Однако отправиться не позже, чем через полторы минуты, он |
|||||||||||||
сможет, если время его прихода попадет на отрезок [C, В]. Долей точек |
|||||||||||||
отрезка [C, В] в отрезке [А, В] можно считать отношение длин этих |
|||||||||||||
отрезков. Таким образом, искомая |
|
y |
|
|
|
||||||||
вероятность Р(А) = |В – C| / |B – А| |
|
|
|
|
|||||||||
= = 1,5/4 = 3/8.♦ |
|
|
|
|
|
21 |
|
|
|
|
|||
Пример |
|
5. |
|
Два |
человека |
|
|
|
|
||||
независимо друг от друга решили |
|
|
|
|
|
||||||||
отдохнуть в любую неделю февраля |
|
|
|
|
|
||||||||
на одном и том же горнолыжном |
|
|
|
|
|
||||||||
курорте. Какова вероятность, что |
|
|
|
|
|
||||||||
онитамвстретятся? |
|
|
|
|
7 |
|
|
|
|
||||
Введем |
двумерную |
декартову |
|
|
|
|
|||||||
систему |
координат |
XOY. |
Пусть |
|
|
|
|
|
|||||
пространство элементарных событий |
|
|
|
|
|
||||||||
Ω = {x,y}, 0 ≤ x ≤ 21, 0 ≤ y ≤ 21, гдеx - |
0 |
|
7 |
21 |
x |
||||||||
время (в сутках) приезда на курорт |
|
||||||||||||
|
|
Рис.2. |
|
|
|||||||||
первогоотдыхающего, аy - второго. |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
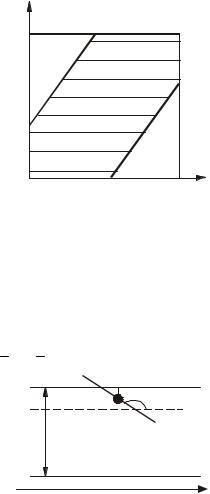
Графически пространству Ω соответствует квадрат со стороной, |
|||||||||||||
равной 21 (рис.2). Чтобы отдыхающие встретились, разность между х и y |
|||||||||||||
должна |
быть |
не |
более |
семи |
суток, т.е. |x – y| ≤ 7 или |
–7 ≤ у– х≤ 7. |
|||||||
Графически этому событию соответствует фигура, координаты точек |
|||||||||||||
которой удовлетворяют неравенству x – 7 ≤ y ≤ x + 7. Искомая вероятность |
|||||||||||||
равна отношению площади заштрихованной фигуры к площади всего |
|||||||||||||
квадрата: |
|
|
|
|
|
|
|
|
|
|
|
|
|
P(A) = ((21)2 −(21−7)2 )/ 212 = |
2 |
2 |
5 |
. |
|
|
|||||||
1− |
= |
9 |
|
|
|||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
♦ |
|
|
|
|
|
|
|
ρ |
α |
|
Пример |
|
6 |
|
(Задача |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
Бюффона). |
|
На |
|
плоскость, |
|
|
L |
|
|
||||
разлинованную |
|
линиями, |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
параллельными |
оси |
ОХ |
и |
|
|
|
|
|
|||||
отстоящими друг от друга на |
|
|
|
|
|
||||||||
расстояние |
L, |
наугад |
бросают |
0 |
|
|
|
x |
|||||
иголку |
длины |
l |
(l < L). |
Какова |
|
Рис.3. |
|
||||||
|
|
|
|||||||||||
вероятность |
того, |
|
что |
|
иголка |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
ρ |
|
|
пересечетоднуизлиний? |
|
|||
|
|
|
|
Будем |
считать |
иголку |
|
L/2 |
|
|
|
|
|||
|
|
отрезком длины l. Пусть α - угол |
|||||
|
|
|
|||||
|
|
|
наклона этого отрезка к оси ОХ, |
||||
|
|
|
ρ - расстояние от середины иглы |
||||
l/2 |
|
|
до ближайшей линии, 0 ≤ α < π, |
||||
l sin α |
|
0 ≤ ρ ≤ L/2 (рис.3). Игла пересечет |
|||||
ρ ≤ |
|
||||||
|
одну |
из линий тогда и |
только |
||||
|
2 |
|
тогда, когда ρ ≤ l/2 (sin α). |
|
|||
0 |
|
|
|
||||
|
π H |
|
|
Введем двумерную |
систему |
||
Рис.4. |
|
координат |
α0ρ |
(рис.4). |
|||
Пространство |
элементарных |
исходов |
представляет |
собой |
|||
прямоугольник, |
состоящий |
|
из |
точек |
{(α, ρ), |
||
0 ≤ α < π, 0 ≤ ρ ≤ L/2}. |
|
|
|
|
|
|
|
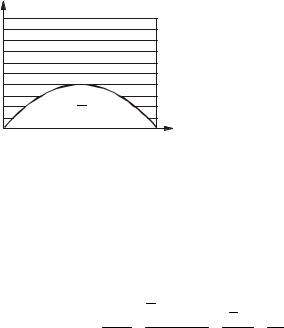
Благоприятные исходы - это множество точек этого прямоугольника, |
|||||||
которые расположены не выше синусоиды. Доля таких точек в |
|||||||
прямоугольнике может быть определена как отношение площади под |
|||||||
синусоидойкплощадипрямоугольника. Следовательно, |
|
||||||
|
2l |
π |
|
|
|
|
|
|
∫sin αdα |
|
l 2 |
= 2l . ♦ |
|
||
P(A) = S(A) = |
0 |
|
= |
2 |
|
||
|
S |
πL / 2 |
|
πL / 2 |
πL |
|
|
§ 6. Аксиоматическое построение теории вероятностей
В случае с геометрическими вероятностями пространство элементарных исходов не конечно и даже не счетно, а значит, невозможно применять классическую формулу для подсчета вероятностей. Проблема определения вероятностей, когда классическая формула неприменима, была решена А.Н.Колмогоровым, который в 1929 г. сформулировал аксиоматику теории вероятностей. Работы Колмогорова в области теории вероятностей считаются самым крупным вкладом в математическую науку вХХстолетии. Вчемэтааксиоматика состоит?
Пусть пространство элементарных событий Ω есть произвольное множество, ипустьА- некоторая системаегоподмножеств.
Аназываетсяалгеброй, если:

1) |
ΩΑ; |
|
|
||
2) |
для любых множеств B, |
C, принадлежащих А, B C |
так же |
||
принадлежит А; |
|
|
|||
3) если B A , тои |
|
Α . |
|
|
|
B |
|
B, C , |
|||
Из |
этих свойств следует, |
что для любых множеств |
|||
принадлежащих А, их пересечение B ∩C А (так как B ∩C = B UC ).
Таким образом, алгебра А - это класс множеств, замкнутый относительно операций дополнения, объединения и пересечения.
Замечание. Алгебра А может быть замкнута не только относительно конечного числа этих операций, но также относительно их счетного числа. В этом случае она называется σ- алгеброй.
Если задано множество Ω и какая-нибудь алгебра его подмножеств А, то говорят, что задано измеримое пространство
(Ω, А).
Пример 7. В примере 4 пространство Ω состоит из точек отрезка [А, В]. Совокупность множеств { Ω, , [C, В], [А, C)} образует алгебру А.♦
Для того чтобы формализовать какую-либо вероятностную задачу, надо соответствующему эксперименту приписать измеримое пространство (Ω, А). Ω означает множество элементарных исходов эксперимента, алгебра А выделяет класс событий. Все остальные подмножества Ω, которые не вошли в алгебру А, cобытиями в данном эксперименте не являются.
Пусть (Ω, А) - измеримое пространство. Вероятностью на измеримом пространстве (Ω, А) называется числовая функция Р, определенная на множествах из А и удовлетворяющая трем аксиомам:
1)для любого множества B А: P(B) ≥ 0 ;
2)P(Ω) =1 ;
3)для любых двух событий В и С, принадлежащих алгебре А, и
таких, что B ∩C = : P(B C) = P(B) + P(C) .
Замечание. Если А является σ-алгеброй, третье утверждение должно выполняться не только для конечного, но для любого
