§16. Решение задачи на собственные функции и собственные значения для оператора

Оператор импульса – оператор с непрерывным спектром собственных значений.

(16.1)

Мы рассматриваем координатное представление, тогда - функция координат.

Оператор векторный, он имеет три компоненты:

Например:

(16.2)

Тогда уравнение (16.1) разбивается на три независимых члена, т.к. операторы коммутируют. Существует утверждение, что еслиможно представить в виде суммы коммутирующих операторов:

,,

то задача на собственные функции и собственные значения распадается на подзадачи этих коммутаторов:

Для задачи (16.1) имеем:

,

где i принимает значения 1,2,3

Решим случай i=1, тогда

(16.3)

Подставляем (16.2) в (16.3) и временно опустим индекс pxу, тогда имеем

т.к. - функция одной переменной, то:

здесь - число, собственное значение.

При решении задачи получили, что pимеет непрерывный спектр на всей числовой оси. Т. е.- не квантуется. Найдем. Используем условие ортонормированности:

В нашем случае:

,

Тогда:

(16.4)

.

.

Обозначим .

.

Тогда

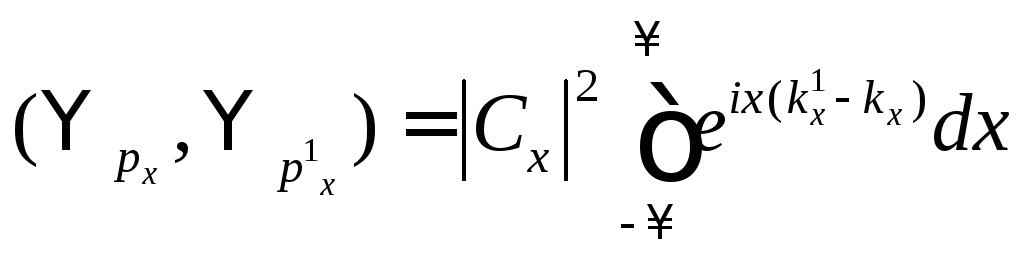
Интеграл дает с точностью до множителя - функцию, поскольку:

Используем следующее свойство -функции:

.

В нашем случае получим

,

тогда

(16.5)

Сравнивая (16.5) и (16.4) получим:

В связи с тем, что волновые функции в квантовой механике определены с точностью до фазового множителя, то

.

Фаза точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким образом: .Мы получили

Теперь запишем - для трёх мерного случая:

(16.6)

Функция (16.6) удовлетворяет условию нормировки (16.4).

В импульсном представлении:

§17. Решение задачи на собственные функции и собственные значения для оператора .

Если в классической механике рассматривать , то

.

Если полученному выражению поставить в соответствие оператор в квантовой механике, то он может быть записан в виде:

,

где - угол поворота вокруг оси.

Рассмотрим задачу на собственные функции и собственные значения для оператора :

,

Мы накладываем на функцию условие периодичности, т. к. уголменяется отдо, т. е.:

Используя данное ограничение можно записать:

,

где NиMцелые числа, значиттоже должно быть целым:

,

где - целое безразмерное число. Из условия периодичности получили квантованность проекции орбитального момента на осьz. Спектр собственных значений оператора дискретный. Так какцелое число, то функцияприобретает индекс:

Найдем константу . Запишем условие нормировки:

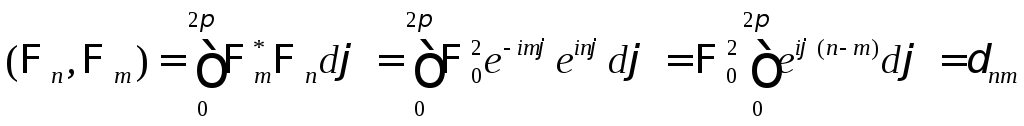
При интеграл дает. В результате получаем выражение для:

Тогда имеем для уравнения собственную волновую функцию

Таким образом, спектр собственных значений оператора дискретный, а собственные функции нормируемые.

§ 18. Вычисление коммутаторов, содержащих операторы

Для оператора :

Найдем , где- есть функцияи, т.е.- координатное представление.

Подействуем этим коммутатором на некоторую произвольную функцию :

(18.1)

Аналогичный результат для оператора в импульсном представлении:

, (18.2)

здесь .

Рассмотрим частные случаи формул (18.1) и (18.2):

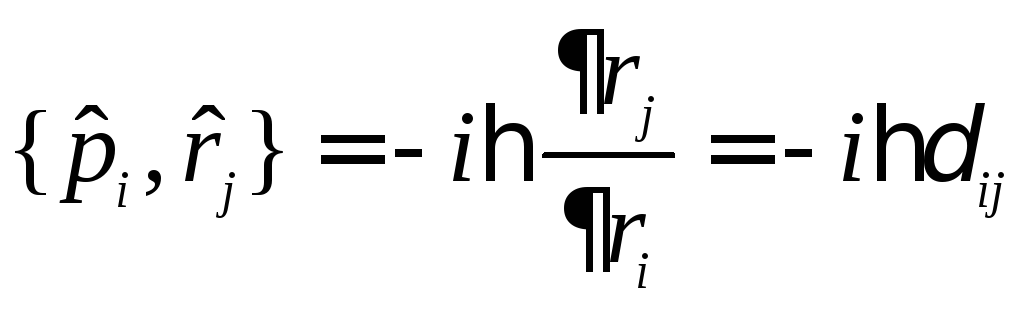1. , здесьиграет роль функции.

2. 

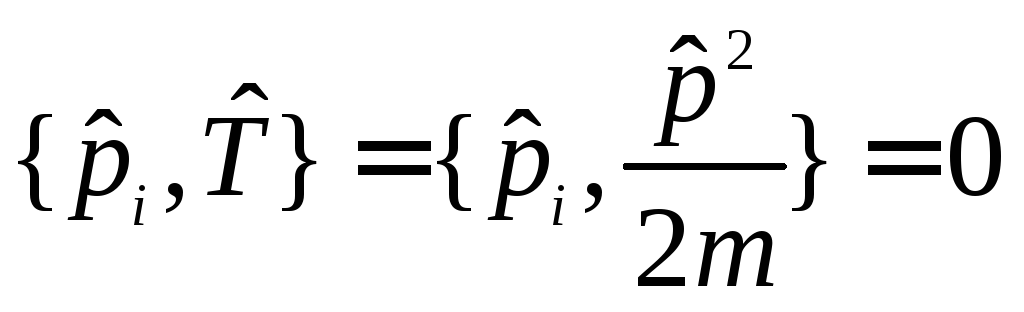
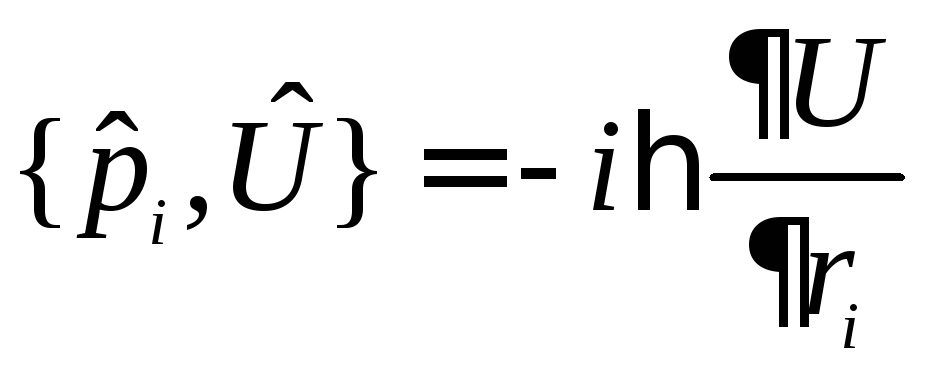3. , здесь 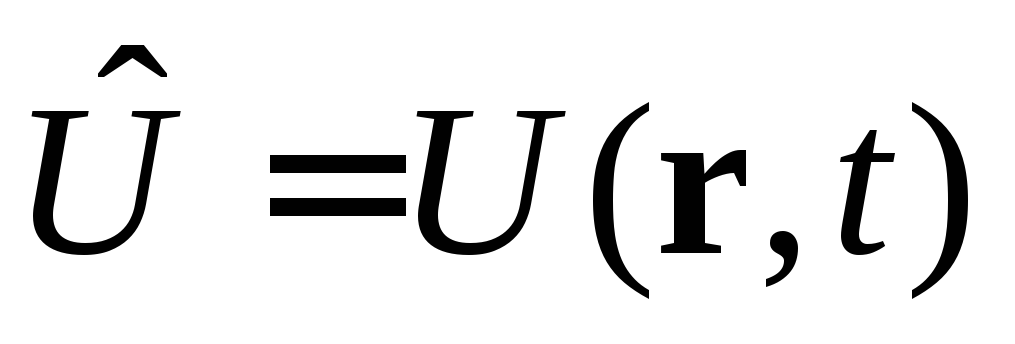потенциальная энергия - функция координат и времени.

3a.

4. 

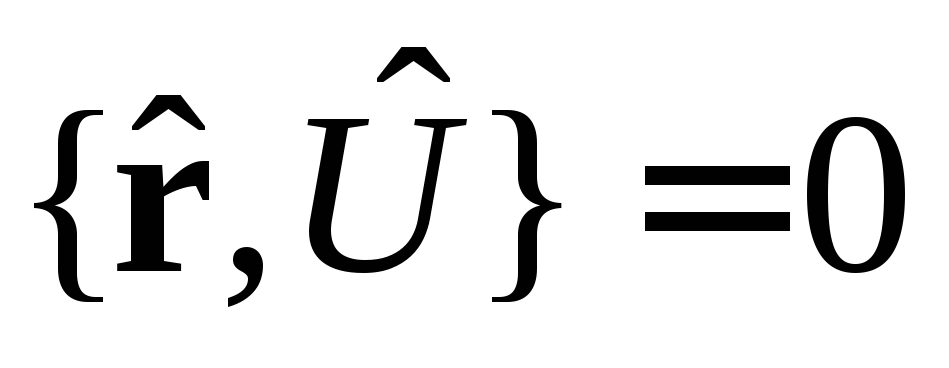
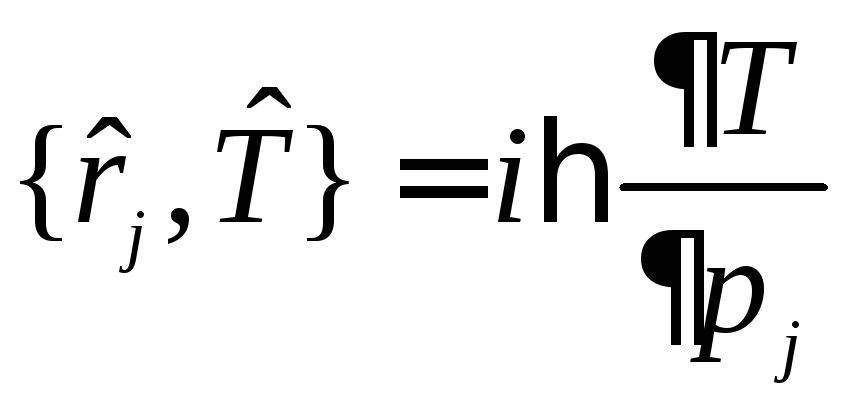5. , здесь импульсное представление, таким образом .

5a..Для одной материальной точки, тогда:

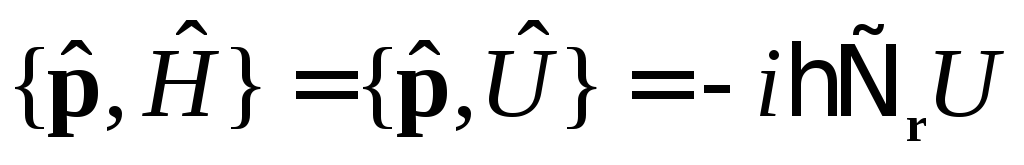6. -координатное представление.

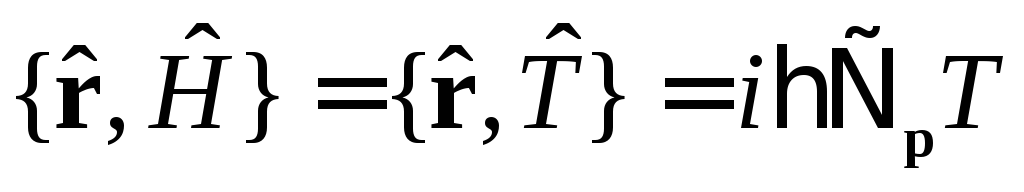7. -импульсное представление.

Рассмотрим соотношение для оператора

Используем дополнительное соотношение:

{используем (18.1) и (18.2):,}{, тогда второе слагаемое} ={в классической математике измерение компонента вектора при бесконечно малом повороте:

,

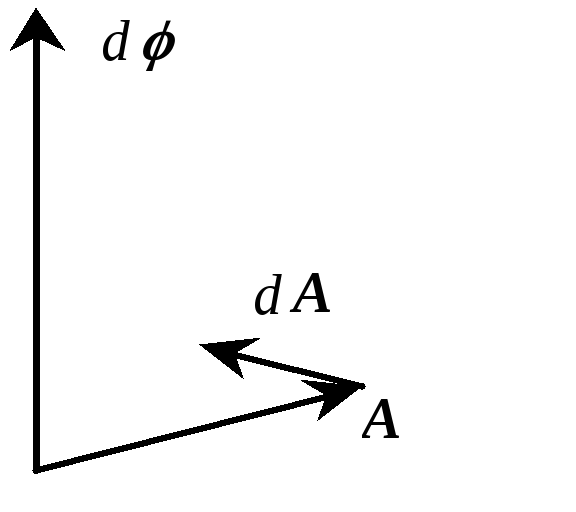
это отношение справедливо и в квантовой теории поля:

}={}={,

. В общем случае импульс и координата не коммутируют, тогда функция координат и импульсов и импульс, координата и функция координат и импульсов не коммутируют. Еслиf – функция скалярная, тогда она не меняется при вращении. В этом случае, чтобы, тоf– векторная функция.}(гдеf есть компонента некоторой векторной величины, т. е..

Тогда перепишем в виде:

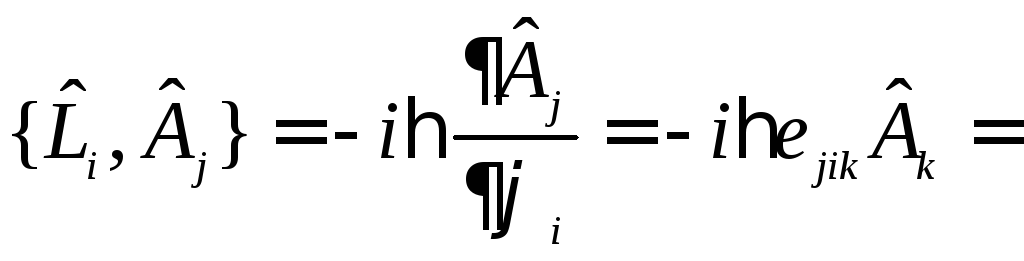{меняем местами индексы}

Тогда для любой векторной функции имеем:

Здесь вместо можно подставить, например,

- коммутаторс любым скаляром равен нулю.

Получим: