1.7. Используя ду 1-го порядка, найти уравнение кривой с заданными свойствами.

В общем случае уравнение кривой имеет вид: =0, где − параметр семейства кривых. Дифференциальное уравнение 1-го порядка может быть записано в виде =0. Геометрический смысл переменных − координаты произвольной точки кривой, геометрический смысл производной − тангенс угла наклона касательной в точке .

Простейшие геометрические задачи с использованием дифференциальных уравнений 1-го порядка можно построить, записывая равенства типа: =, гдепроизвольнаяфункция. Самый простой случай, когда=.

Мы будем применять более содержательный принцип построения дифференциальных уравнений. Представим себе, исследователя заинтересовали некоторые геометрические свойства кривой линии, и он хочет, с помощью дифференциальных уравнений, найти выражение функции, соответствующей этой линии.

На рисунке представлена некоторая кривая =0. Для произвольной точкиэтой кривой построены касательнаяи нормальи выделены точки пересечения касательной и нормали с осямии, именно: а) для касательной: точкии; б) для нормали: точкии.

В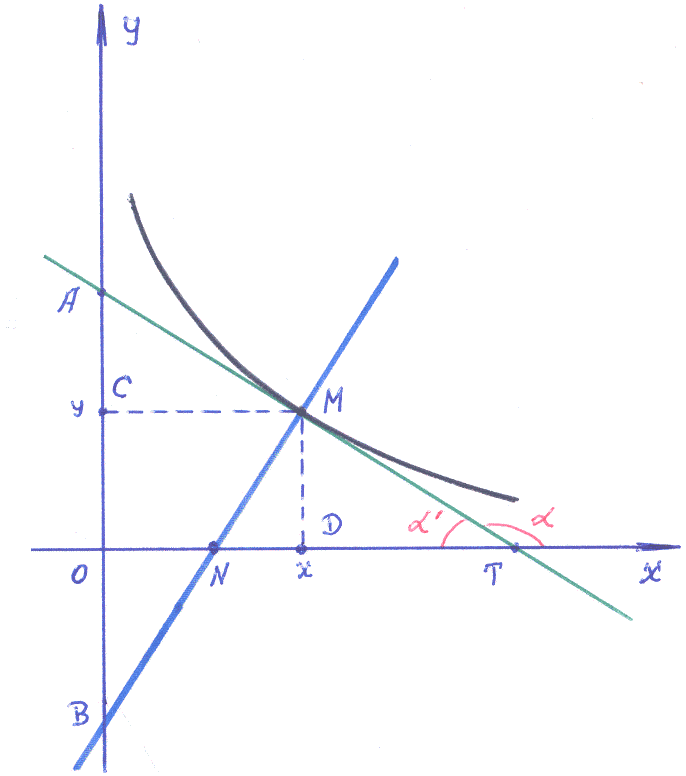общем случае рассматривают задачи, представляемые равенствами, в которые входят длины отрезков кривой:,,,,,,и– отрезки касательной,– подкасательная,и– отрезки нормали,– поднормаль. Каждое такое равенство есть дифференциальное уравнение, определяющее совокупные геометрические свойства кривой. Решая уравнение, находят соответствующее семейство кривых с заданными свойствами. Задавая начальные условия, из семейства кривых выделяют единственную кривую.

Замечание. В предлагаемых Заданиях отрезки , и , не используются: их вычисление не представляет особого труда и (при желании) каждый может построить примеры с использованием названных отрезков. Рис. 1.1.

Общая задача. В соответствии с рисунком определим характерные отрезки кривой ,,,,,, обозначив угловой коэффициент касательной в точке величиной.

Решение:

1). Запишем уравнение касательной для точки : . (1.8)

2). Запишем уравнение нормали для точки : . (1.9)

3). Определим координаты точек и пересечения касательной, представленной в виде выражения (1.8), с осями координат , ; вычислим ,:

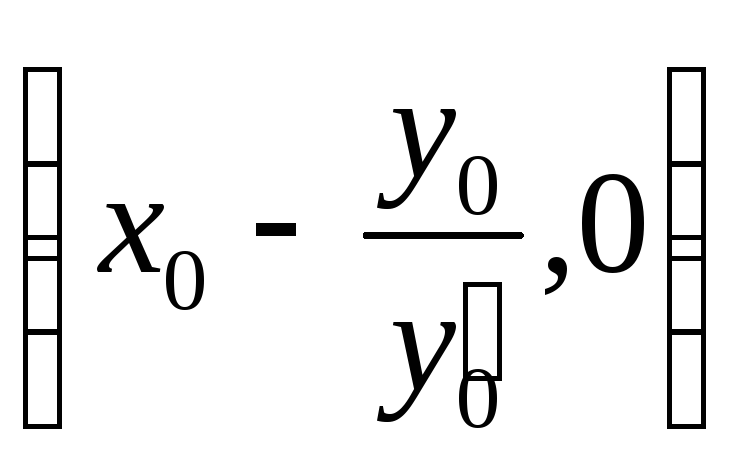а) для точки имеем:=0 → = → = → =; (1.10)

б) для точки имеем: =0 → = → = → =. (1.11)

4). Используя (1.10), вычислим длину подкасательной: =. (1.12)

5). Определим координаты точек и пересечения нормали, представленной в виде выражения (1.9), с осями координат , ; вычислим ,:

а) для точки имеем:=0 → = → = → =; (1.13)

б) для точки имеем: =0 → = → = → =. (1.14)

6). Используя (1.13), вычислим длину поднормали: =.

Ответ: Определены все упомянутые точки и отрезки.

Замечание: Формулы (1.8)(1.14) используют координаты выделенной точки , но записанные соотношения выполняются для любой точки кривой линии. При определении свойств некоторой линии мы будем использовать совокупные свойства характерных отрезков ,,,,, по отношению ко всем её точкам! Это значит, что в формулах (1.8)(1.14) индекс, отмечающий использование точки не должен применяться!

Пример 1.7. Найти уравнение кривой, проходящей через точку (1,1), зная, что длина отрезка, отсекаемого на оси ординат касательной к кривой в каждой точке, пропорционален ординате точки касания. Принять коэффициент пропорциональности=2.

Решение:

На Рис. 1.2, в соответствии с условием Примера, выделены (красный цвет) отрезки (отсекаемый на оси ординат касательной) и (ордината произвольной точки кривой). Показана касательная к кривой в точке .

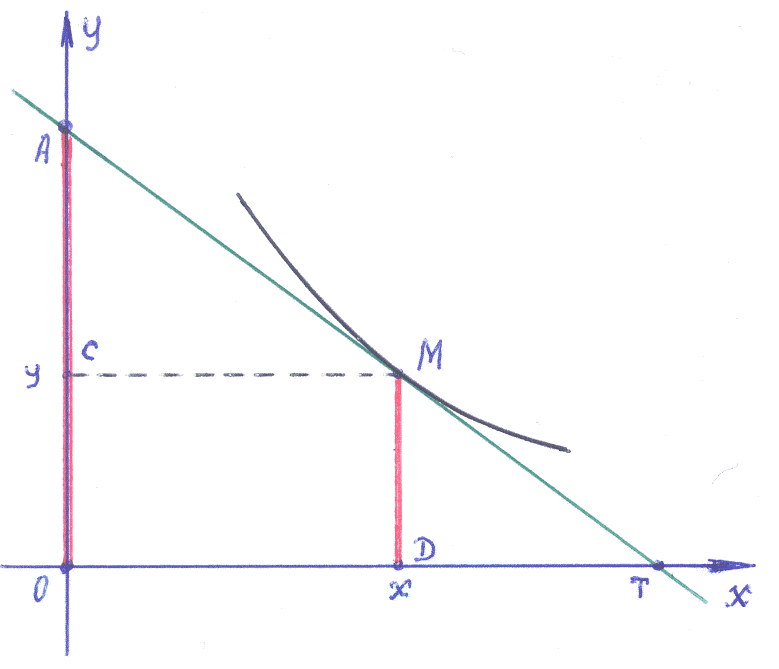
Рис. 1.2.

Учитывая условие задачи, для произвольной точки кривой необходимо записать: =2, или =2 (используется формула (1.8) общей геометрической задачи). Это значит, что рассматриваются только кривые, расположенные в верхней полуплоскости относительно оси , так как необходимо .

Из равенства =2 следует, что необходимо рассмотреть два случая:

▪ Случай-1: ;

▪ Случай-2: .

Случай-1.

1). Дифференциальное уравнение имеет очевидное решение: – функция, которой соответствует ось . Это решение не отражают существа поставленной «геометрической задачи» и мы его не будем учитывать.

2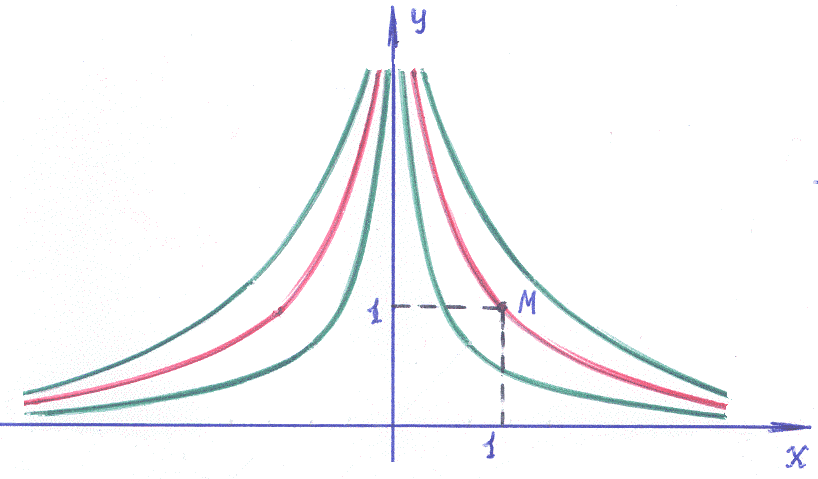). Запишем уравнение в виде – уравнение с разделяющимися переменными, общее решение которого может быть представлено в виде функции: – семейство гипербол. Требование означает: если → , если → . На рисунке точка выделяет из семейства гипербол единственную кривую. Рис. 1.3.

Случай-2.

1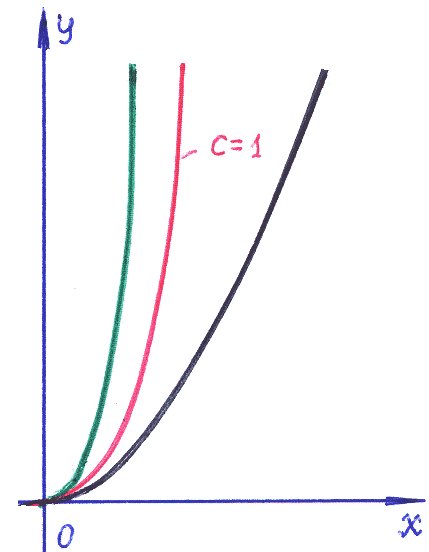). И в этом случае решение также учитывать не будем. Перепишем уравнение в виде: .

2). Нетрудно получить его общее решение: – семейство кубических парабол. Здесь также: если → , если → .

3). Показано, что кривая содержит точку при =1. Для значений семейство интегральных кривых не показано!

Рис. 1.4.

Ответ: для случая-1: общее решение , частное ; для случая-2: общее решение , частное.

Общие сведения. Далее рассматривается 6 типов Примеров по применению дифференциальных уравнений в геометрии. Каждый из Примеров использует параметры так, что в соответствующем Задании нужно заменить параметр указанным в Задании значением и оформить (в соответствии с образцом!) решение.

Тип-1: Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания, то есть:.

Общая схема решения задачи и образец оформления:

1). Запишем заданное уравнение в виде: . Это линейное уравнение, записанное в стандартной форме, где,.

2). Применяем подстановку: . Вычисляем интеграл: ==, записываем функцию:=.

4). Вычисляем интеграл:=+=+=+изаписываем общее решение задачи: =·.

5). Используя начальные условия (задача Коши), находим: =и записываем частное решение уравнения:=·.

Ответ:=·– общее решение; частное:=·.

Тип-2: Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на число, при условии, что.

Общая схема решения задачи и образец оформления:

1). Так как длина подкасательной =, то уравнение в виде:=. Из уравнения следует, что. Это значит, что для значенийточкаи интегральная кривая должны располагаться в правой полуплоскости. Если, используется левая полуплоскость.

2). Так как число может быть и положительным, и отрицательным, необходимо рассматривать два случая: ▪ Случай-1: →=;

▪ Случай-2: → =.

Случай-1.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:=.

Ответ:– общее решение; частное решение:=.

Случай-2.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:=.

Ответ:– общее решение; частное решение:=.

Замечание.В каждом из случаев для полученного частного решения необходимо указать область определения и область значений функции.

Тип-3: Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на число, при условии, что.

Общая схема решения задачи и образец оформления:

1). Так как длина подкасательной =, то уравнение в виде:=. Из уравнения следует, что. Это значит, что для значенийточкаи интегральная кривая должны располагаться в верхней полуплоскости. Если, используется нижняя полуплоскость.

2). Так как число может быть и положительным, и отрицательным, необходимо рассматривать два случая: ▪ Случай-1: →=;

▪ Случай-2: → =.

Случай-1.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:– семейство прямых линий.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:.

Ответ:– общее решение; частное решение:.

Случай-2.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:– семейство прямых линий.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:.

Ответ:– общее решение; частное решение:.

Замечание.В каждом из случаев для полученного частного решения необходимо указать область определения и область значений функции.

Тип-4: Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на число, при условии, что.

Общая схема решения задачи и образец оформления:

1). Так как длина подкасательной =, то уравнение в виде:=. Из уравнения следует, что. Это значит, что для значенийточкаи интегральная кривая должны располагаться в правой полуплоскости. Если, используется левая полуплоскость.

2). Так как число может быть и положительным, и отрицательным, необходимо рассматривать два случая: ▪ Случай-1: →;

▪ Случай-2: → .

Случай-1.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Его общее решение может быть записано в виде:– семейство гипербол.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:=.

Ответ:– общее решение; частное решение:=.

Случай-2.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Его общее решение может быть записано в виде:– семейство эллипсов.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:=.

Ответ:– общее решение; частное решение:=.

Замечание.В каждом из случаев для полученного частного решения необходимо указать область определения и область значений функции.

Тип-5: Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на число, при условии, что.

Общая схема решения задачи и образец оформления:

1). Так как длина подкасательной =, то уравнение в виде:=. Из уравнения следует, что. Это значит, что для значенийточкаи интегральная кривая должны располагаться в верхней полуплоскости. Если, используется нижняя полуплоскость.

2). Так как число может быть и положительным, и отрицательным, необходимо рассматривать два случая: ▪ Случай-1: →;

▪ Случай-2: → .

Случай-1.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:– семейство прямых линий.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:.

Ответ:– общее решение; частное решение:.

Случай-2.

3). Запишем уравнение в виде:– уравнение с разделяющимися переменными. Так как, в соответствии с исходной записью, необходимо, то. Это значит, можем записать:. Его общее решение может быть записано в виде:– семейство прямых линий.

4). Используя начальные условия (задача Коши), находим:=и записываем частное решение уравнения:.

Ответ:– общее решение; частное решение:.

Замечание.В каждом из случаев для полученного частного решения необходимо указать область определения и область значений функции.

Тип-6: Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на число, при условии, что.

Общая схема решения задачи и образец оформления:

1). Запишем заданное уравнение в виде: . Это уравнение с разделяющимися переменными. Его общее решение:– семейство кубических парабол.

2). Используя начальные условия (задача Коши), находим: =и записываем частное решение уравнения:.

Ответ:– общее решение; частное:.

Задание 1.7. Найти уравнения кривых:

Замечание: 1). В каждом Задании показать на рисунке семейство кривых (4-5 линий), соответствующее общему решению дифференциального уравнения, среди которых выделено частное решение: линия, проходящая через заданную точку!

2). Используя кривую частного решения, показать на чертеже касательную и подкасательную, нормаль и поднормаль для заданной точки .

1.7.1.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.2.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на число 2.

1.7.3.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.4.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.5.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.6.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.7.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на число 4.

1.7.8.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.9.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.10.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.11.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.12.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.13.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен абсциссеточки касания, умноженной на число −2.

1.7.14.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.15.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.16.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.17.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.18.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.19.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на число 2.

1.7.20.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.21.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.22.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.23.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.24.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.25.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен ординатеточки касания, умноженной на число −2.

1.7.26.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на число −2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.27.Найти уравнение линии, проходящей через точкузная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на число −2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.28.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на число −2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.29.Найти уравнение линии, проходящей через точкузная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на число 2. Рассмотреть только случай, когда в каждой точке кривой:.

1.7.30.Найти уравнение линии, проходящей через точкузная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2.

Внимание.Задания по геометрии оформляются отдельным документом и подлежат коллективной защите: коллектив формируется по признаку типа Задания.