
- •Пределы и непрерывность
- •1.1.2. Точные грани множества
- •1.1.3. Существование точных граней
- •§ 1.2. Предел последовательности
- •Предельные точки и предел последовательности
- •Свойства предела последовательности
- •Арифметические свойства предела последовательности
- •§ 1.3. Монотонные последовательности
- •1.3.1. Предел монотонной ограниченной последовательности
- •1.3.2. Бесконечно большие последовательности
- •1.3.4. Число е
- •1.3.5. Теорема о вложенных стягивающихся отрезках
- •§ 1.4. Сходящиеся подпоследовательности
- •1.4.1. Теорема Больцано-Вейерштрасса
- •1.4.2. Критерий Коши сходимости последовательности.
- •Литература
Пределы и непрерывность
Числовые множества.
Последовательности, предел последовательности
Лекции 1-2
1.1. Числовые множества
1.1.1. Ограниченные множества
Определение.
Множество
![]() называетсяограниченным
сверху,
если существует число
называетсяограниченным
сверху,
если существует число
![]() такое, что для всех
такое, что для всех![]() выполняется неравенство
выполняется неравенство![]() При этом число
При этом число![]() называетсяверхней
гранью множества
называетсяверхней
гранью множества
![]()
Если
![]() является верхней гранью
множества
является верхней гранью
множества
![]() то любое число
то любое число
![]() также является верхней гранью множества
также является верхней гранью множества![]()
Определение.
Множество
![]() называетсяограниченным
снизу,
если существует число
называетсяограниченным
снизу,
если существует число
![]() такое, что для всех
такое, что для всех![]() выполняется неравенство
выполняется неравенство![]() При этом число
При этом число![]() называетсянижней
гранью множества
называетсянижней
гранью множества
![]()
Если
![]() является нижней гранью
множества
является нижней гранью
множества
![]() то любое число
то любое число
![]() также является нижней гранью множества
также является нижней гранью множества![]()
Определение.
Множество
![]() называетсяограниченным,
если существует число
называетсяограниченным,
если существует число
![]() такое, что для всех
такое, что для всех![]() выполняется неравенство
выполняется неравенство![]()
Множество
![]() является ограниченным тогда и только
тогда, когда оно ограниченно и сверху
и снизу.
является ограниченным тогда и только
тогда, когда оно ограниченно и сверху
и снизу.
Определение.
Число
![]() называетсянаибольшим
(наименьшим)
элементом
множества
называетсянаибольшим
(наименьшим)
элементом
множества
![]() если
если![]() и для всех
и для всех![]() выполняется неравенство
выполняется неравенство![]() (
(![]() ).
).
Наибольший
(наименьший) элемент множества
![]() является его верхней (нижней) гранью.
Если существует верхняя (нижняя) грань
множества
является его верхней (нижней) гранью.
Если существует верхняя (нижняя) грань
множества![]() принадлежащая
принадлежащая![]() то у
то у![]() существует наибольший (наименьший)
элемент.
существует наибольший (наименьший)
элемент.
Пример.
а)
Множество
![]() является ограниченным снизу, неограниченным
сверху, неограниченным, имеет наименьший
элемент, равный 2, не имеет наибольшего.
является ограниченным снизу, неограниченным
сверху, неограниченным, имеет наименьший
элемент, равный 2, не имеет наибольшего.
б)
Множество
![]() является ограниченным снизу, ограниченным
сверху, ограниченным, имеет наименьший
элемент, равный 2, не имеет наибольшего.
является ограниченным снизу, ограниченным
сверху, ограниченным, имеет наименьший
элемент, равный 2, не имеет наибольшего.
1.1.2. Точные грани множества
Определение.
Точной
верхней гранью (или
супремумом)
множества
![]() называется
наименьшая из его верхних граней.
Обозначается
называется
наименьшая из его верхних граней.
Обозначается![]()
Если
![]() то, во-первых,
то, во-первых,![]() является верхней гранью
является верхней гранью![]() во-вторых, любое число
во-вторых, любое число![]() не является верхней гранью, то есть:
не является верхней гранью, то есть:
Для любого
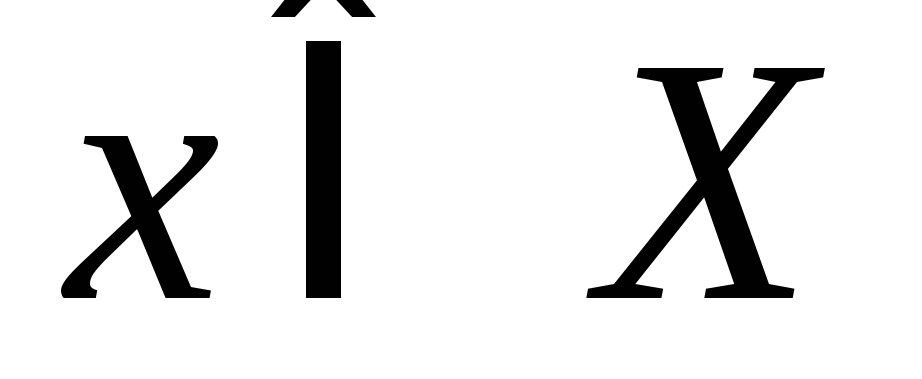 выполняется неравенство
выполняется неравенство
Для любого
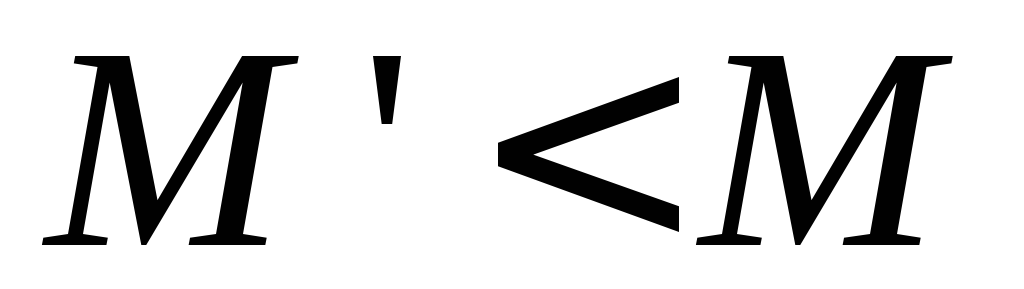 найдется
найдется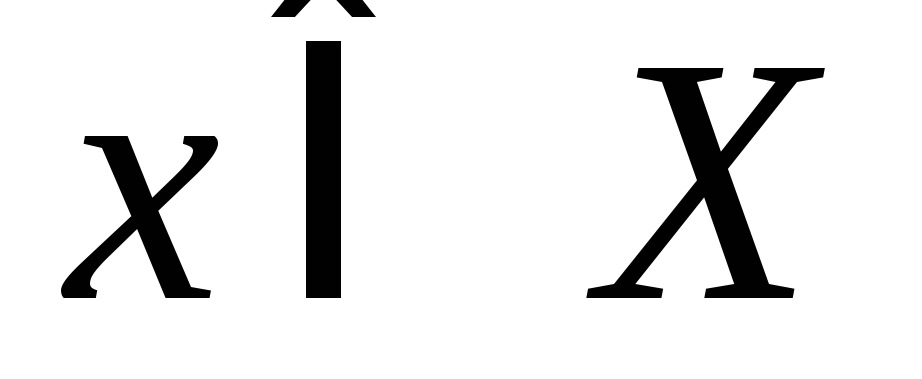 такой,
что
такой,
что
Обозначив
![]() получим другую запись пункта 2:
получим другую запись пункта 2:
Для любого
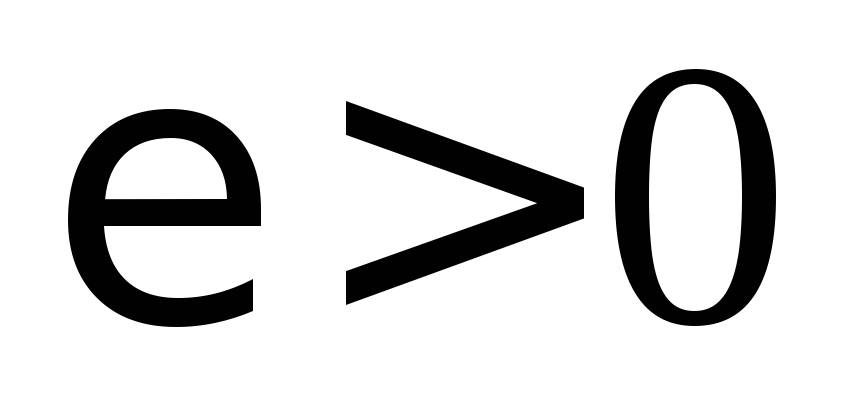 найдется
найдется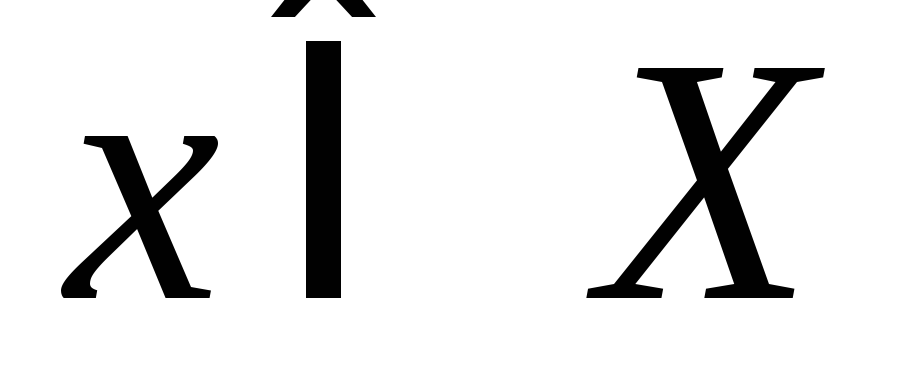 такой,
что
такой,
что
Определение.
Точной
нижней гранью (или
инфимумом)
множества
![]() называется
наибольшая из его нижних граней.
Обозначается
называется
наибольшая из его нижних граней.
Обозначается![]()
Если
![]() то, во-первых,
то, во-первых,![]() является нижней гранью
является нижней гранью![]() во-вторых, любое число
во-вторых, любое число![]() не является нижней гранью, то есть:
не является нижней гранью, то есть:
Для любого
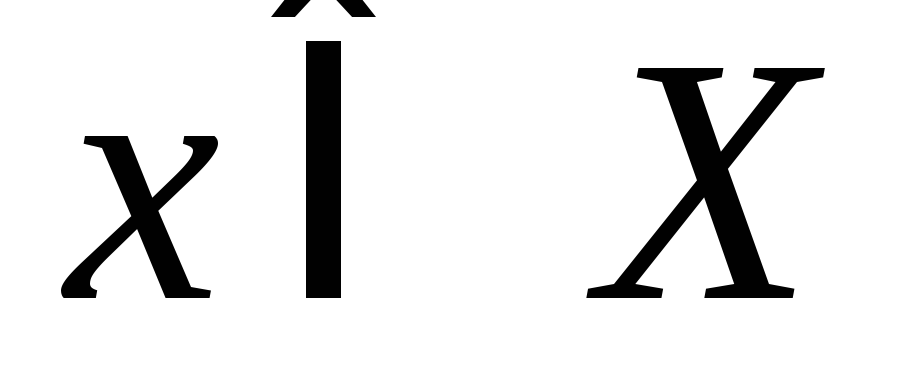 выполняется неравенство
выполняется неравенство
Для любого
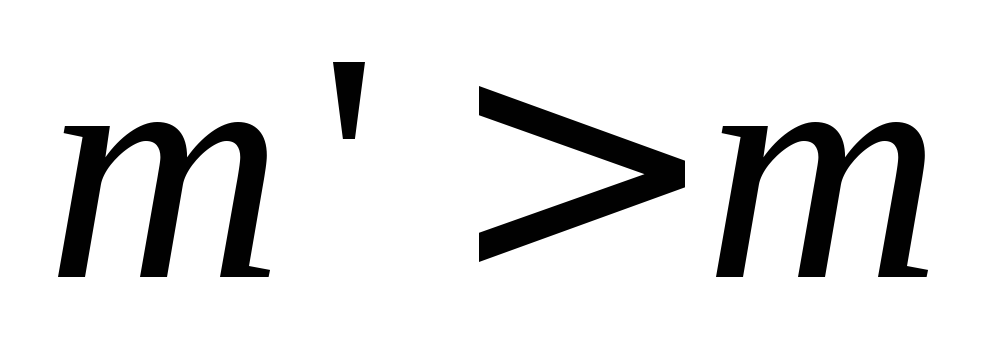 найдется
найдется такой,
что
такой,
что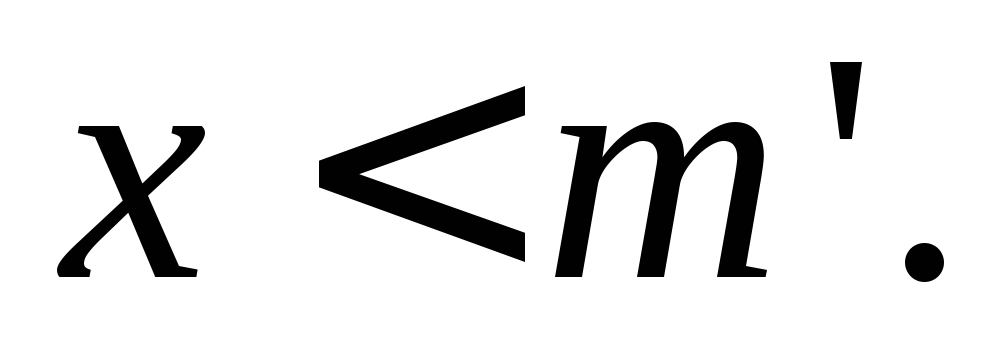
Обозначив
![]() получим другую запись пункта 2:
получим другую запись пункта 2:
Для любого
 найдется
найдется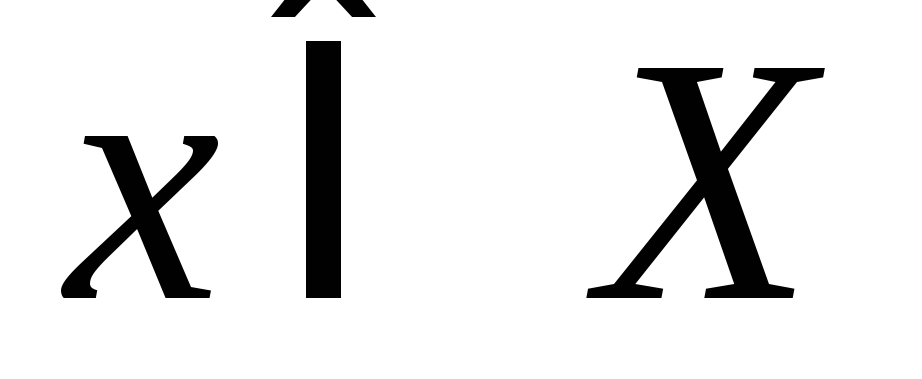 такой,
что
такой,
что
Пример.
Множеством
верхних граней множества
![]() является множество
является множество![]() Наименьшим элементом множества
Наименьшим элементом множества![]() является 3,
является 3,![]() Множеством нижних граней множества
Множеством нижних граней множества![]() является множество
является множество![]() Наибольшим элементом множества
Наибольшим элементом множества![]() является 2,
является 2,![]()
Множеством,
противоположным множеству
![]() называется
множество, обозначаемое
называется
множество, обозначаемое![]() состоящее из элементов
состоящее из элементов![]() где
где![]()
Суммой
множеств
![]()
![]() называется множество, обозначаемое
называется множество, обозначаемое![]() состоящее из всевозможных сумм
состоящее из всевозможных сумм![]() где
где![]()
![]()
![]()
![]()
Теорема.
Если
множество
![]() имеет супремум, то множество
имеет супремум, то множество![]() имеет инфимум и
имеет инфимум и![]()
Доказательство.
Обозначим
![]() Тогда для любого
Тогда для любого![]() выполняется неравенство
выполняется неравенство![]() Так как для любого
Так как для любого![]() найдётся
найдётся![]() такой, что
такой, что![]() то для любого
то для любого![]() выполняется
неравенство
выполняется
неравенство![]() Возьмём произвольно
Возьмём произвольно![]() Тогда найдётся
Тогда найдётся![]() такой, что
такой, что![]() а значит,
а значит,![]() значит, найдётся
значит, найдётся![]() такой, что
такой, что![]() Тем самым доказано, что
Тем самым доказано, что![]()
![]()
Упражнение.
Доказать,
что если множество
![]() имеет инфимум, то множество
имеет инфимум, то множество![]() имеет супремум и
имеет супремум и![]()
Теорема.
Если
множества
![]()
![]() имеют супремум, то множество
имеют супремум, то множество![]() также имеет супремум и
также имеет супремум и![]()
Доказательство.
Обозначим
![]()
![]() Произвольное
Произвольное![]() представимо в виде
представимо в виде![]() где
где![]()
![]() Тогда выполняются неравенства
Тогда выполняются неравенства![]()
![]() Значит,
Значит,![]() Зададим произвольно
Зададим произвольно![]() Тогда найдутся
Тогда найдутся![]() и
и![]() такие, что
такие, что![]()
![]() Тогда для элемента
Тогда для элемента![]() выполняется неравенство
выполняется неравенство![]() Тем самым доказано, что
Тем самым доказано, что![]()
Следствие.
Если
множества
![]()
![]() имеют инфимум, то множество
имеют инфимум, то множество![]() также имеет инфимум и
также имеет инфимум и![]()
Доказательство.
Множества
![]() и
и![]() имеют супремум, при этом
имеют супремум, при этом![]()
![]() Тогда их сумма, равная
Тогда их сумма, равная![]() имеет супремум,
имеет супремум,![]() Множество
Множество![]() имеет инфимум,
имеет инфимум,![]()
![]()
Разностью
двух множеств
![]() и
и![]() называется сумма множеств
называется сумма множеств![]() и
и![]()
Упражнение.
Доказать,
что если множество
![]() имеет супремум, а множество
имеет супремум, а множество![]() имеет инфимум, то множество
имеет инфимум, то множество![]() имеет супремум, а множество
имеет супремум, а множество![]() имеет инфимум. При этом выполняются
равенства
имеет инфимум. При этом выполняются
равенства![]()
![]()
